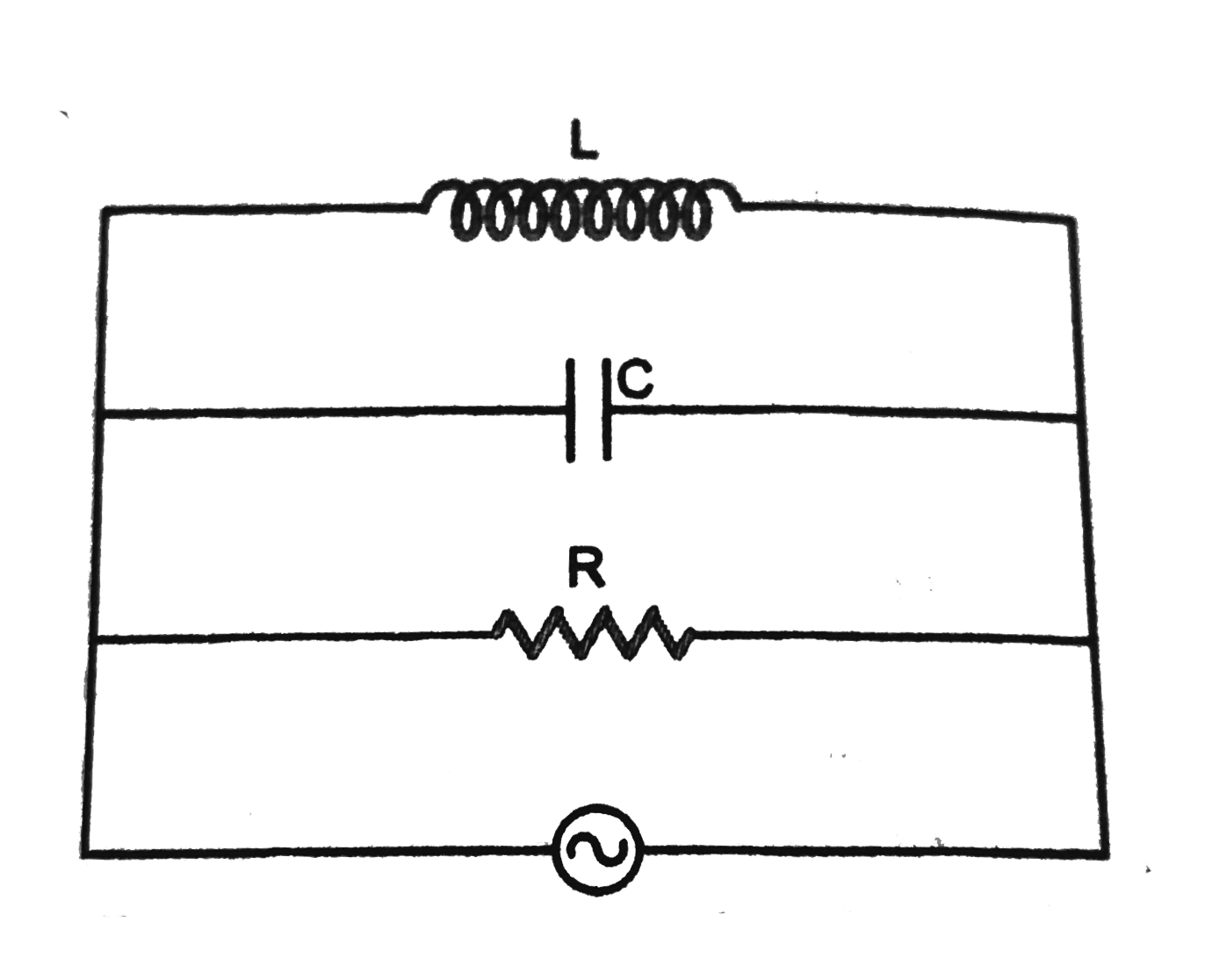
Keeping the source of frequency equal to the resonating frequency of the series LCR circuit, if the three elements L, C and R in are arranged in parallel , show that the total current in the parallel LCR circuit is a minimum at this frequency. Obtain the r.m.s. value of current in each branch of the circuit for the elements and source specified in for this frequency.

Video Solution

Text Solution

Verified by Experts

Inductor (L),a capacitor (C),and a resistor (R) is connected in parallel with each other in a circuit where,
L=5.0H
C=80 $μ F$ = $80 \times 10^{- 6} F$
$R = 40 Ω$
Potential of the voltage source, $V = 230 V$
Impedance (Z) of the given parallel LCR circuit is given as:
$\frac{1}{2} = \sqrt{\frac{1}{R^{2}} + {(\frac{1}{ω L} - ω C)}^{2}}$
where,
$ω =$ Angular frequency
At resonance, $\frac{1}{ω L} - ω C = 0$
$∴ ω = \frac{1}{\sqrt{L C}}$
$= \frac{1}{\sqrt{5 \times 80 \times 10^{- 6}}} = 50$ rad/s
Hence, the magnitude of Z is the maximum at 50 rad/s . As a result at the total current is minimum.
Rms current flowing through inductor L is given as:
$I_{L} = \frac{V}{ω L}$
$= \frac{230}{50 \times 5} = 0.92 A$
Rms current flowing through capacitor C is given as:
$I_{C} = \frac{V}{A} = ω C V$
$ω C$
$= 50 \times 80 \times 10^{- 6} \times 230 = 0.92 A$
Rms current flowing through resistor R is given as:
$I_{R} = \frac{V}{R}$
$= \frac{230}{4} = 5.75 A$

Updated on:21/07/2023

At resonance frequency the impedance in series LCR circuit is
Amaximum
Bminimum
Czero
Dinfinity
The resonant frequency of a series LCR circuit with $L = 2.0 H, C = 32 μ F$ and $R = 10 Ω$ is
A20 Hz
B30 Hz
C40 Hz
D50 Hz
To reduce the resonant frequency in an $L C R$ series circuit with a generator
Athe generator frequency should be reduced
Banother capacitor should be added in parallel to the first
Cthe iron core of the inductor should be removed
Ddielectric in the capacitor should be removed.