Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by v2=2gh(1+k2/R2) using dynamical consideration (i.e. by consideration of forces and torque). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Let a rolling body (l=Mk2) rolls down an inclined plane with an initial velocity u=0, When it reaches the bottom of inclined plane, let its linear velocity be v. Then from conservation ofmechanical energy, we have Loss in P.E. =Gain in translationa K.E. +Gain in rotational K.E.
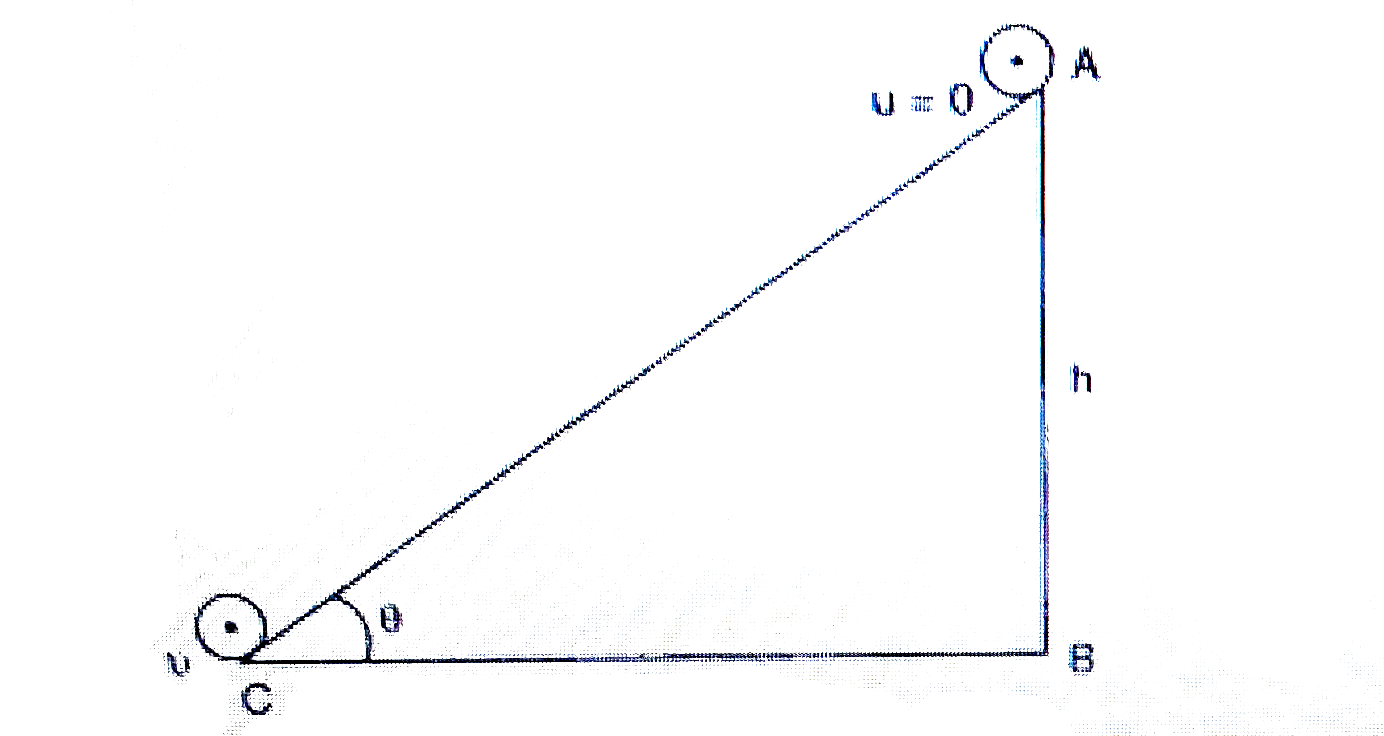
∴ Mgh=12mv2+12Iω2
=12mv2+12(mk2)(v2R2)
∴ Mgh=12mv2(1+k2R2)
⇒ v2=2gh(1+k2R2)
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:NCERTChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:EXERCISE
Explore 33 Videos
- PHYSICAL WORLD Book:NCERTChapter:PHYSICAL WORLD Exercise:EXERCISE
Explore 16 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERTChapter:THERMAL PROPERTIES OF MATTERExercise:EXERCISE
Explore 22 Videos
Similar Questions
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclied plane of a hight h is given by v2=2gh(1+k2/R2) using dynamical consideration (i.e. by consideration of forces and torque). Note k i sthe radius of gyration of the body about its symmentry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
View SolutionThe radius of gyration of a disc about its own axis is is R√2 The radius of gyration about its diameter is- - - - -
View Solution
Knowledge Check
The radius of gyration of a sphere of radius R about a tangent is.
A√23RB√25RC√53RD√75RThe radius of gyration of a solid sphere of radius R about its tangential is
A√75RB√25RC√57DRThe radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is
A2 mB2 cmC1 mD0.2 m
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
View SolutionThe radius of gyration of a disc about an axis coinciding with a tangent in its plane is
View SolutionThe radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point R2 away from the centre of the sphere is:
View SolutionThe radius of gyration of a solid cylinder of mass M and radius R about its own axis is
View SolutionA body rolls without slipping. The radius of gyration of the body about an axis passing through its centre of mass is K. The radius of the body is R. The ratio of rotational kinetic energy to translational kinetic energy is.
View Solution

