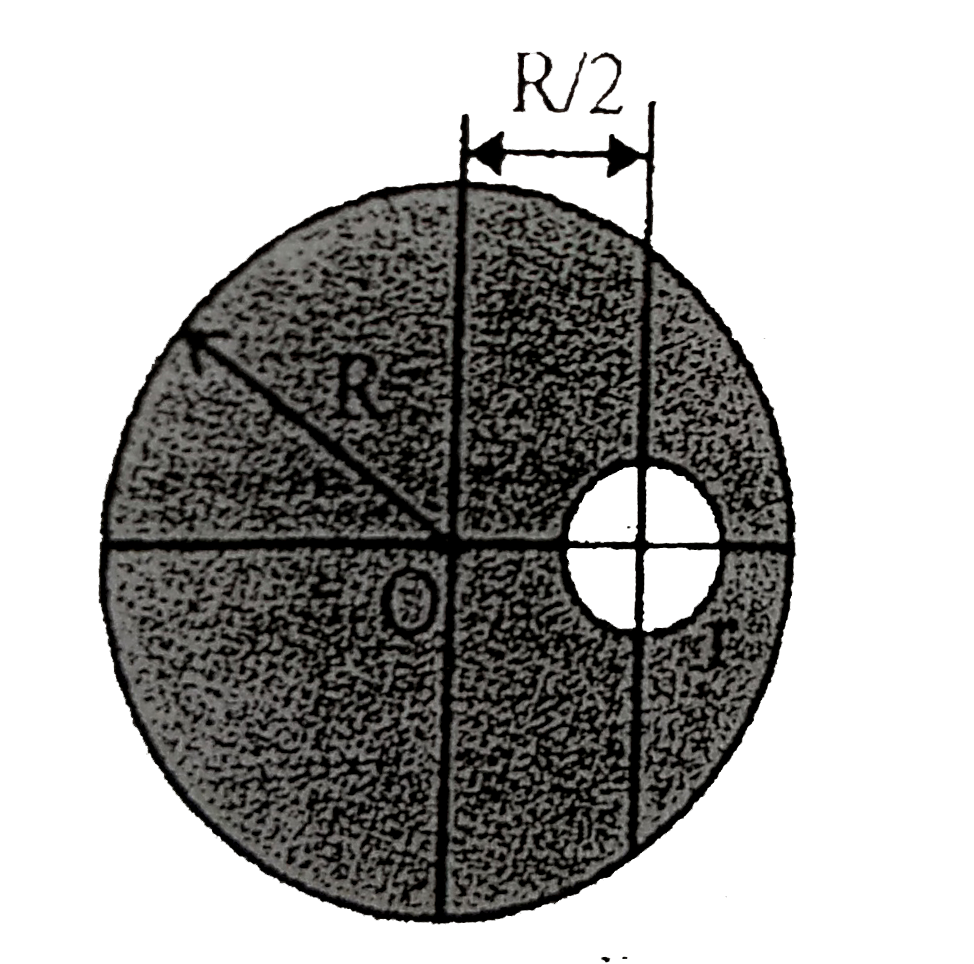
From a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
Let from a bigger uniform disc of radius R with centre O a smaller circular hole of radius R/2 with its centre at O1 (where R OO1=R/2) is cut out. Let centre of gravity or the centre of mass of remaining flat body be at O2, where OO2=x. If σ be mass per unit area, then mass of whole disc M1=TTR2σ and mass of cut out part
M2=π(R2)2σ=14πR2σ=M14
x=M1×(0)−M2(OO1)M1−M2=0−M14×R2M1−M14=−R6
i.e., O2 is at a distnce R/6 from centre of disc on diametrically opposite side to centre of hole.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERTCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERTCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERTCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
From a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View Solution
Knowledge Check
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
A circular section of radius r si cut out of a uniform disc of radius R, the centre of the hole being R/2 from the centre of the original disc. Locate the centre of gravity of the remainder.
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View SolutionFind the centre of mass of a unifrom disc of radius a from which a circulr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
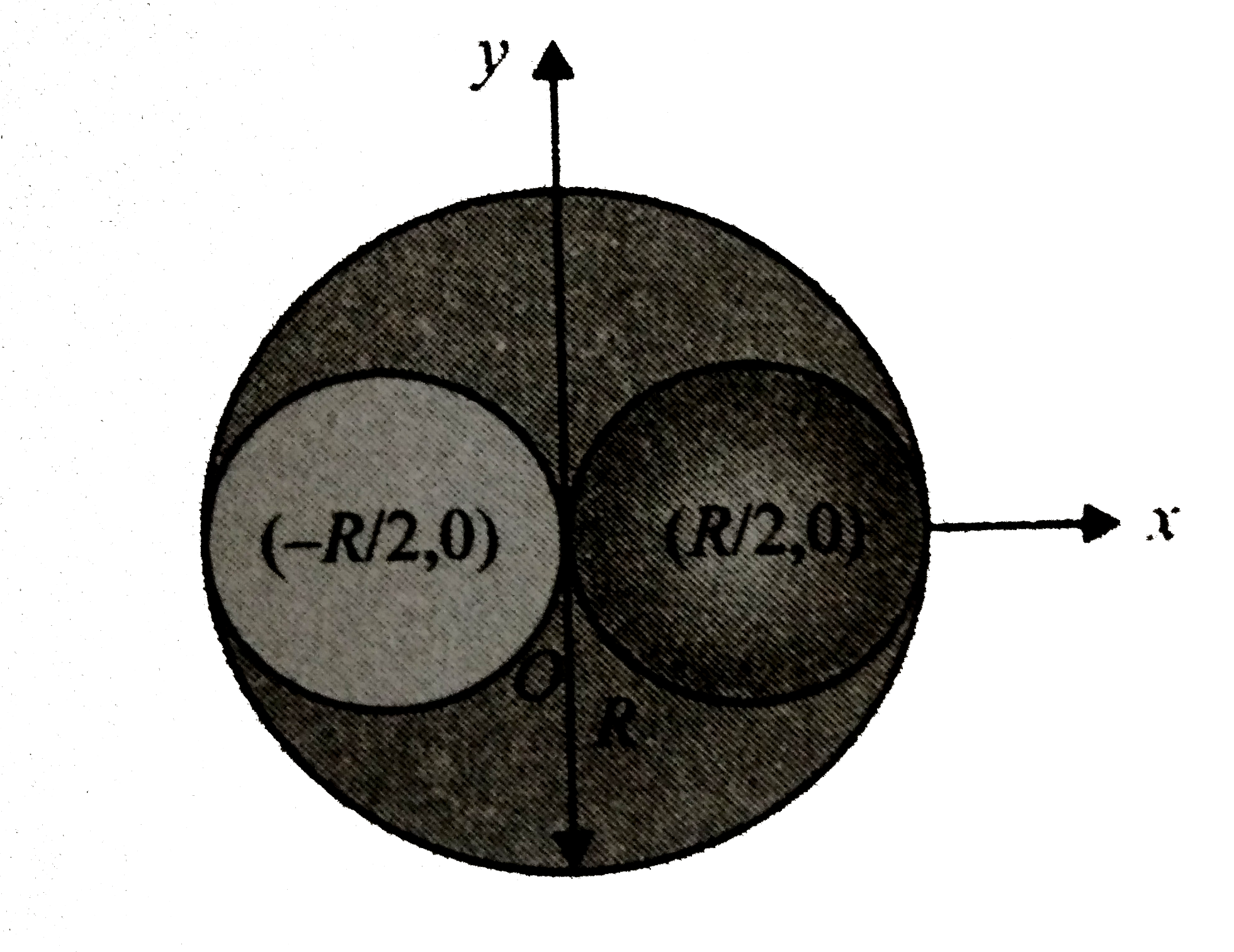
View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.
View Solution
