एम्पीयर के नियम का उपयोग करते हुए अनन्त लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र का व्यंजक प्राप्त कीजिए।

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

ऐम्‍पियर के नियम से अनन्त लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र- नीचे दिये गये चित्र में किसी अनन्त लम्बाई अर्थात अत्यधिक लम्बाई का सीधा चालक तार है जिसमें I धारा प्रवाहित हो रही है।
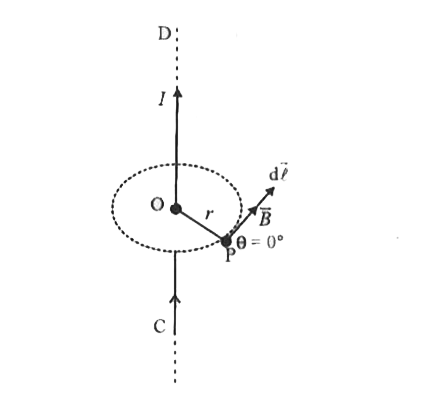
ocr_image
इससे r दूरी पर एक बिंदु P‌ स्थित है जिस पर हमें चुम्बकीय क्षेत्र के मान की गणना करनी है । तार की लम्बाई दूरी r के सापेक्ष अत्यधिक होने से तार को अनन्त लम्बाई का माना जा सकता है। इसके लिए हम r त्रिज्या का वृत्त, तार के चारों ओर खींचते हैं ओर बिंदु P पर एक लम्बाई के अल्पांश की हम कल्पना करते हैं।
चित्र से स्पष्ट है कि चुम्बकीय क्षेत्र →B की दिशा तथा अल्पांश
→dl की दिशा एक ही है।
ऐम्‍पियर के नियम से
∮→B.→dl=μ0Σi
यहां पर μ0 निर्यात या वायु के लिए पारगम्यता गुणांक है।
∮B.dlcosθ=μ0I ∵Σi=I
यहां पर →B तथा →dl एक ही दिशा में है।
अतः θ=0∘ लेने पर
⇒∮B.dlcos0∘=μ0I
⇒∮B.dl=μ0I
⇒B∮dl=μ0I
B×2πr=μ0I[∵∮dl=परिधि=2πr]
या B=μ0I2πr……1
इस चुम्बकीय क्षेत्र की दिशा को दक्षिण हस्त नियम से ज्ञात करते हैं।
स्पष्ट है कि अनन्त लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र →B का परिमाण
a प्रवाहित धारा I के समानुपाती अर्थात B∝I
(b) चालक से लम्बवत दूरी r के व्युत्क्रमानुपाती होती है।
अर्थात →B में दूरी के साथ परिवर्तन को चित्र में दर्शाया गया है।
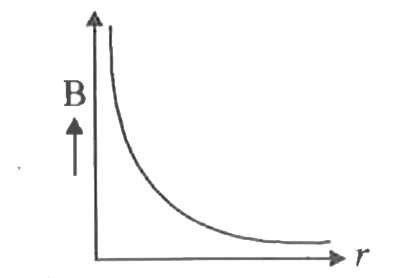
ocr_image
चित्र- चालक से लम्बवत दूरी (r) के साथ B में परिवर्तन

Updated on:21/07/2023
|
Class 12PHYSICSMOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions