बायो सावर्ट नियम लिखिए। इसकी सहायता से एक वृत्ताकार धारावाही कुण्डली के अक्ष पर स्थित बिंदु पर चुम्बकीय क्षेत्र के लिए व्यंतजक व्युत्पन्न कीजिए।
बायो सावर्ट नियम- इस नियम के अनुसार एक धारावाही अल्पांश →δl के कारण, निर्वात या वायु में स्थित किसी बिंदु A(r,θ) पर उत्पन्न चुम्बकीय क्षेत्र ∣∣δ→B0∣∣ का मान निम्न बातों पर निर्भर करता है।

(i)∣∣∣δ−−→B0∣, चालक में प्रवाहित धारा I के समानुपाती होता है।
∣∣δ→B0∣∣∝I………..1
(ii) ∣∣δ→B0∣∣ अल्पांश की लम्बाई ∣∣→δl∣∣ के समानुपाती होता है।
∣∣δ→B0∣∣∝∣∣→δl∣∣…….2
(iii) ∣∣δ→B0∣∣ अल्पांश् के केंद्र से अभीष्ट बिंदु की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
∣∣δ→B0∣∣∝1r2……..3
(iv) ∣∣δ→B0∣∣ अल्पांश के केंद्र को अभीष्ट बिंदु से जोड़ने पर बने कोण की जया के समानुपाती होता है।
∣∣δ→B0∣∣∝sinθ…………4
इसलिए समीकरण 1, 2, 3 तथा 4 से
∣∣δ→B0∣∣∝(1∣∣→δl∣∣)sinθr2
या ∣∣δ→B0∣∣=μ04πI∣∣→δl∣∣sinθr2
यहां μ0=4π×107 वेबर/ ऐम्पियर मीटर निर्वात का पारगम्यता गुणांक कहलाता है। वायु या निर्वात से भिन्न माध्यम के लिए चुम्बकीय क्षेत्र
∣∣δ→B0∣∣=μ4π1∣∣→δl∣∣sinθr2 …………..5
जहां पर μ=μ0μr माध्यम की पारगम्यता कहलाता है।
वृत्ताकार धारावाही कुण्डली की अक्ष पर चुम्बकीय क्षेत्र
आगे चित्र में a त्रिज्या की एक वृत्ताकार कुण्डली है जो कि yz तल में स्थित है। इसमें I की धारा प्रवाहित हो रही है। इस कुण्डली का अक्ष X दिशा की ओर है जिस पर x दूरी पर स्थित किसी बिंदु P पर चुम्बकीय क्षेत्र ज्ञात करना है।
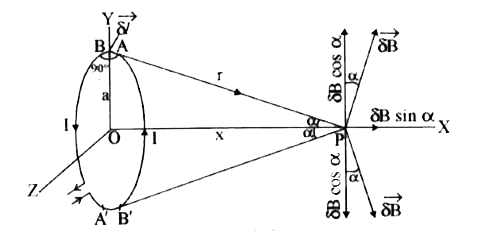
कुण्डली को छोटे- छोटे अल्पांशों में बाटा गया है।
माना Ab की लम्बाई δl है इस अल्पांश से P की दूरी r है। P पर चुम्बकीय क्षेत्र
−→δB=μ04π→δl×→rr3 ……….1
δB=μ04πIδlsinθr2 ………..2
θ=90∘ होने पर
δB=μ04πIδlsin90∘r2
δB=μ04πIδlr2 ……………3
AB के कारण अक्ष के लम्बरूप क्षेत्र का घटक परस्पर बराबर एवं विपरीत होने के कारण एक दूसरे को निरस्त कर देते हैं परंतु दोनों के अक्षीय घटक एक ही दिशा में होनें के कारण जुड़ जाते हैं। इसी तरह कुण्डली की पूरी परिधि को व्यासतः अभिमुख अल्पांशों में विभाजित करके समझ सकते हैं।
बिंदु P पर परिणामी चुम्बकीय क्षेत्र, उसकी अक्ष के अनुदिश घटकों के योग के तुल्य होगा अर्थात
B=ΣδBsinα
चित्र से sinα=ar
B=Σμ04πIδlr2×ar
=μ04πIar3Σδl
Σδl=2πa
∴B=μ04πIar3×2πa
B=μ04π×2πa2Ir3……..4
यदि कुण्डली में N फेरे है।
तो B=μ04π×2πa2NIr3वेबर/मी.2
चित्र से r=(a2+x2)1/2
∴r3=(a2+x2)3/2
∴→B=μ04π×2πa2NI(a2+x2)3/2ˆi……5
या →B=μ0NIa22(a2+x2)3/2ˆi टेसला (अक्ष के अनुदिश)
अर्थात +x अक्ष की दिशा में
धारावाही कुण्डली के अक्ष के किसी बिंदु पर चुम्बकीय क्षेत्र समीकरण 4 या 5 से प्राप्त होता है एवं इस क्षेत्र की दिशा अक्ष के अनुदिश होती है।
Topper's Solved these Questions
- विद्युत धारा के चुम्बकीय प्रभावBOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत धारा के चुम्बकीय प्रभावEXERCISE - आंकिक प्रश्न
17 Videos
- विद्युत धारा BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत धारा EXERCISE - उच्चस्तरीय बुद्धि-कौशल प्रश्न
11 Videos
- विद्युत परिपथ BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत परिपथ EXERCISE - उच्चस्तरीय बुद्धि -कौशल प्रश्न
5 Videos
Similar Questions
तार की एक वृत्ताकार कुण्डडली में 100 फेरे हैं प्रत्येक की त्रिज्या 8.0 cm है और इनमें 0.40A विद्युत धारा प्रवाहित हो रही है । कुण्डली के केंद्र पर चुम्बकीय क्षेत्र का परिमाण क्या है?
View Solutionधातु के आयन्स से दो टक्करों के मध्य मुक्त इलेक्ट्रॉन्स द्वारा तय किये गये पथ की प्रकृति क्या होती है?
View Solutionएक विभवमापी के प्राथमिक परिपथ में 0.2A धारा है। विभवमापी के तार का विशिष्ट प्रतिरोध ओर परिच्छेद क्षेत्रफल क्रमशः 4×10−7Ω−m और 8×10−7m2 है। विभव प्रवणता का मान ज्ञात कीजिए।
View Solutionवृत्ताकार धारावाही कुंडली के कारण चुम्बकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
View Solutionवलय के अक्ष पर स्थित बिंदु पर विधुत क्षेत्र की तीव्रता
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
View Solutionधारावाही वलय के अक्ष पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionआंकीक प्रश्न |विद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View SolutionRecap|धारावाही कुंडली के अक्ष पर चुम्ब्कीय क्षेत्र
View SolutionRecap|धारावाही कुंडली के अक्ष पर चुम्ब्कीय क्षेत्र|प्रश्न|Summary
View Solutionवृत्ताकार धारावाही कुंडली के अक्ष पर एक बिंदु पर चुंबकीय क्षेत्र
View Solution
