दो वृत्ताकार धारावाही कुण्डलियों की त्रिज्यायें क्रमशः r1 व r2 तथा फेरों की संख्यायें क्रमशः n1 व n2 हैं। इन्हें श्रेणीक्रम में जोड़ा गया है तब सिद्ध कीजिए कि इनके केंद्रों पर उत्पन्न चुम्बकीय क्षेत्रों का अनुपात n1r2:n2r1 होगा । यदि कुण्डलियां समांतर क्रम में जुड़ी हो तो सिद्ध कीजिए कि केंद्रों पर उत्पन्न चुम्बकीय क्षेत्रों का अनुपात (r2/r1)2 के तुल्य होगा।
श्रेणीक्रम में जुड़े होने से कुण्डलियों में धारा I समान होगी। अतः इनके केंद्रों पर चुम्बकीय क्षेत्र होंगे।
B1=μ0n1I2r1
और B2=μ0n1I2r2∴B1B2=μ0n1I2r1μ0n1I2r2
⇒B1B2=n1r1=r2n2=n1r2r1n2
⇒B2:B2=n1r2:n2r1
समांतर क्रम में जुड़े हाने पर उनमं धाराओं का अनुपात उनके प्रतिरोधों R1 व R2 के अनुपात के व्युत्क्रमानुपाती होगा अर्थात
I1I2=R2R1=n2(2πr2)ρn1(2πr1)ρ=n2r2n1r1
B1B2=μ0n1I12r1×2r2μ0n2I2
=n1r2n2r1×n2r2n1r1=r22r21
Topper's Solved these Questions
- विद्युत धारा के चुम्बकीय प्रभावBOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत धारा के चुम्बकीय प्रभावEXERCISE - आंकिक प्रश्न
17 Videos
- विद्युत धारा BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत धारा EXERCISE - उच्चस्तरीय बुद्धि-कौशल प्रश्न
11 Videos
- विद्युत परिपथ BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत परिपथ EXERCISE - उच्चस्तरीय बुद्धि -कौशल प्रश्न
5 Videos
Similar Questions
तार की एक वृत्ताकार कुण्डडली में 100 फेरे हैं प्रत्येक की त्रिज्या 8.0 cm है और इनमें 0.40A विद्युत धारा प्रवाहित हो रही है । कुण्डली के केंद्र पर चुम्बकीय क्षेत्र का परिमाण क्या है?
View Solutionधातु के आयन्स से दो टक्करों के मध्य मुक्त इलेक्ट्रॉन्स द्वारा तय किये गये पथ की प्रकृति क्या होती है?
View Solutionएक विभवमापी के प्राथमिक परिपथ में 0.2A धारा है। विभवमापी के तार का विशिष्ट प्रतिरोध ओर परिच्छेद क्षेत्रफल क्रमशः 4×10−7Ω−m और 8×10−7m2 है। विभव प्रवणता का मान ज्ञात कीजिए।
View SolutionTwo planets revolve round the sun with frequencies N_(1) and N_(2) revolutions per year. If their average orbital radii be R_(1) and R_(2) respectively, then R_(1)//R_(2) is equal to
View SolutionLet R_(t) represents activity of a sample at an insant and N_(t) represent number of active nuclei in the sample at the instant. T_(1//2) represents the half life. {:(,"Column I",,"Column II"),((A),t=T_(1//2),(p),R_(t)=(R_(0))/(2)),((B),t=(T_(1//2))/(ln2),(q),N_(0)-N_(t)=(N_(0))/(2)),((C),t=(3)/(2)T_(1//2),(r),(R_(t)-R_(0))/(R_(0)) = (1-e)/(e)),(,,(s),N_(t)=(N_(0))/(2sqrt(2))):}
View SolutionValue of 1r21+1r22+1r23+1r2 is :
View SolutionR1 तथा R2 वक्रता -त्रिज्यावाली दो सतहों से घिरे एक लेंस को चित्र के अनुरूप रखा गया है। सिद्ध करें की
n3v−n1u=n2−n1R1+n3−n2R
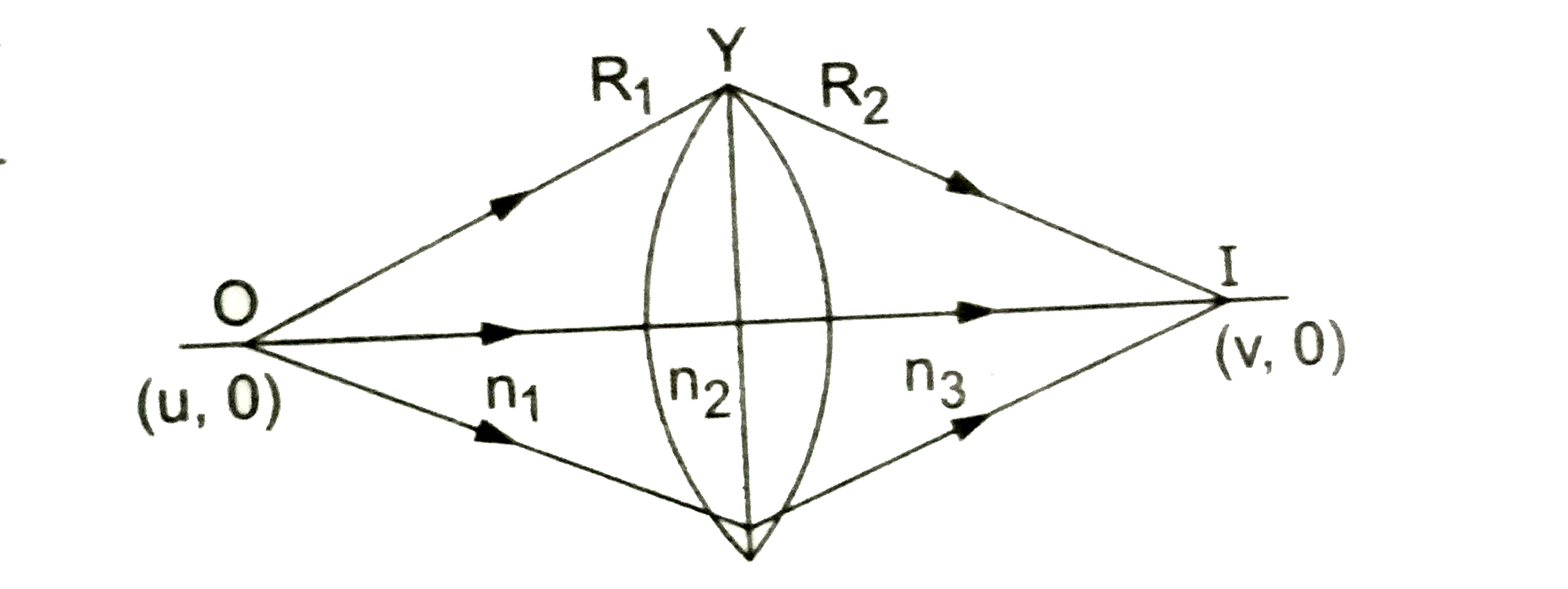
View Solutionमाना कि X={1,2,3,4,5,6,7,8,9}, माना कि X में सम्बन्ध R1 तथा R2 इस प्रकार हैं कि R1={(x,y):x−y,3 से विभाज्य हैं,x≠y} तथा R2={(x,y):{x,y}⊂{1,4,7} या {x,y}⊂{2,5,8} या {x,y}⊂{3,6,9} जहाँ ⊂ का अर्थ उपसमुच्चय से हैं| दिखाएं कि R1=R2
View Solutionयदि दो वृतो की त्रिज्याएँ क्रमशः r1 व r2 है और वे एक - दूसरे को बाह्यतः स्पर्शः करते हो , तो -
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!2
View SolutionIn a ΔABC, if 2r2r3r2−r1=r3−r1 then
r1(r2+r3)√r1r2+r2r3+r3r1=
View Solutionत्रिज्याओं r1 व r2(r1>r2) के दो गोलों को संयोजित किया जाता है। यदि परिणामी ठोस का गुरुत्व केंद्र r1 त्रिज्या वाले गोले के केंद्र से r1+r23 दूरी पर केंद्रों को मिलाने वाली रेखा पर स्थित है। r1:r2 है
View Solutionआकृति में आपको दो वृत्त क्रमशः C(O, r) और C(O' r) दिए गए हैं| यदि उनकी संगत जीवाओं की लम्बाइयों में 1:1 का अनुपात हो तो उनके संगत केंद्रों में अंतरिक कोणों का अनुपात ज्ञात कीजिए |
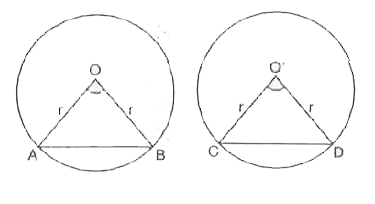
View SolutionTwo coplanar and concentric coils 1 and 2 have respectively the number of turns N1 and N2 and radii r1 and r2(r2>>r1). Deduce the expression for mutual inductance of this system.
View Solution
