Obtain equivalent capacitance of the following network, Fig. For a 300V supply determine the charge and voltage across each capacitor.
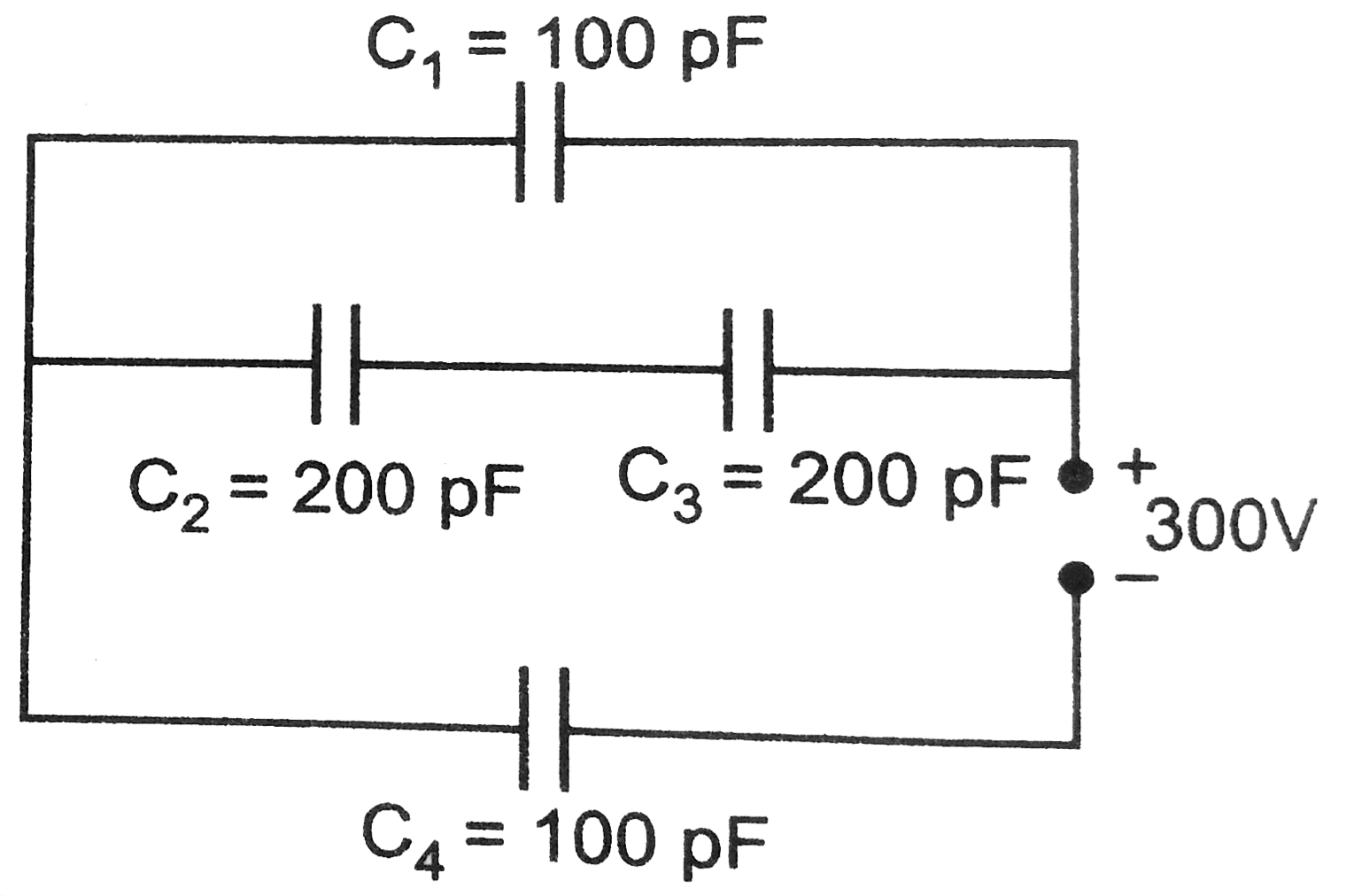
Capacitance of capacitor C1 is 100 pF.
Capacitance of capacitor C2 is 200 pF
Capacitance of capacitor C3 is 200 pF
Capacitance of capacitor C4 is 100 pF
Supply potential, V=300 V
Capacitor C2 and C3 are connected in series. let their equivalent capacitance be C''.
∴1C'=1200+1200=2200
C'=100 pF
Capacitors C1 and C' are in parallel. let their equivalent capacitances be C''
∴C''=C'+C1
=100+100=200pF
C'' and C4 are connected in series . let their equivalent capacitance be C.
∴1C=1C''+1C4
=1200+1100=2+1200
C=2003pF
Hence, the equivalent capacitance of the circuit is 2003pf
potential difference across C''=V''
potential difference across C4=V4
∴V''+V4=V=300V
Charge on C4 is given by
Q4=CV
=2003×10−12×300
=2×10−8C
∴V4=Q4C4
=2×10−8100×10−12=200V
∴ Voltage across C1 is given by
V1=V−V4
=300-200=100 V
Hence , potential difference V1 across C1 is 100 V
charge on C1 is given by
Q1=C1V1
=100×10−12×100
=10−8C
C2 and C3 having same capacitances have a potential difference of 100 V together. since C2 adn C3 are in series, the potential difference across C2 adn C3 given by
V2=V3=50V
Therefore, charge on C4 is given by
Q2=C2V2
=200×10−12×50
=10−8C
And charge on C3 is given by
Q3=C3V3
=200×10−12×50
=10−3C
Hence, the equivalent capacitance of the given circuit is 2003pF with .
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERTChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise
Explore 37 Videos
- ELECTROMAGNETIC WAVESBook:NCERTChapter:ELECTROMAGNETIC WAVESExercise:Exercise
Explore 15 Videos
- MAGNETISM AND MATTERBook:NCERTChapter:MAGNETISM AND MATTERExercise:Exercise
Explore 25 Videos
Similar Questions
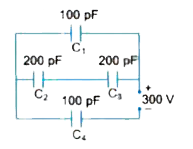
Obtain equivalent capacitance of the following net work, Fig. For a 300V supply determine the charge and voltage across each capacitor.

View SolutionObtain the equivalent capacitance of the network in Fig. For a 300 V supply, determine the charge and voltage across each 100 pF capacitor.
View Solution
Knowledge Check
In the circuit shown in figure find

a. the equivalent capacitance
b. the charge stored in each capacitor and
c. the potential difference across each capacitor.A1.2μF 120μC 60Vand40VB1.2μF 120μC 60Vand20VC1.2μF 12μC 60Vand40VD12μF 120μC 60Vand40V
Find the equivalent capacitance between A and B for the following network of capacitors.

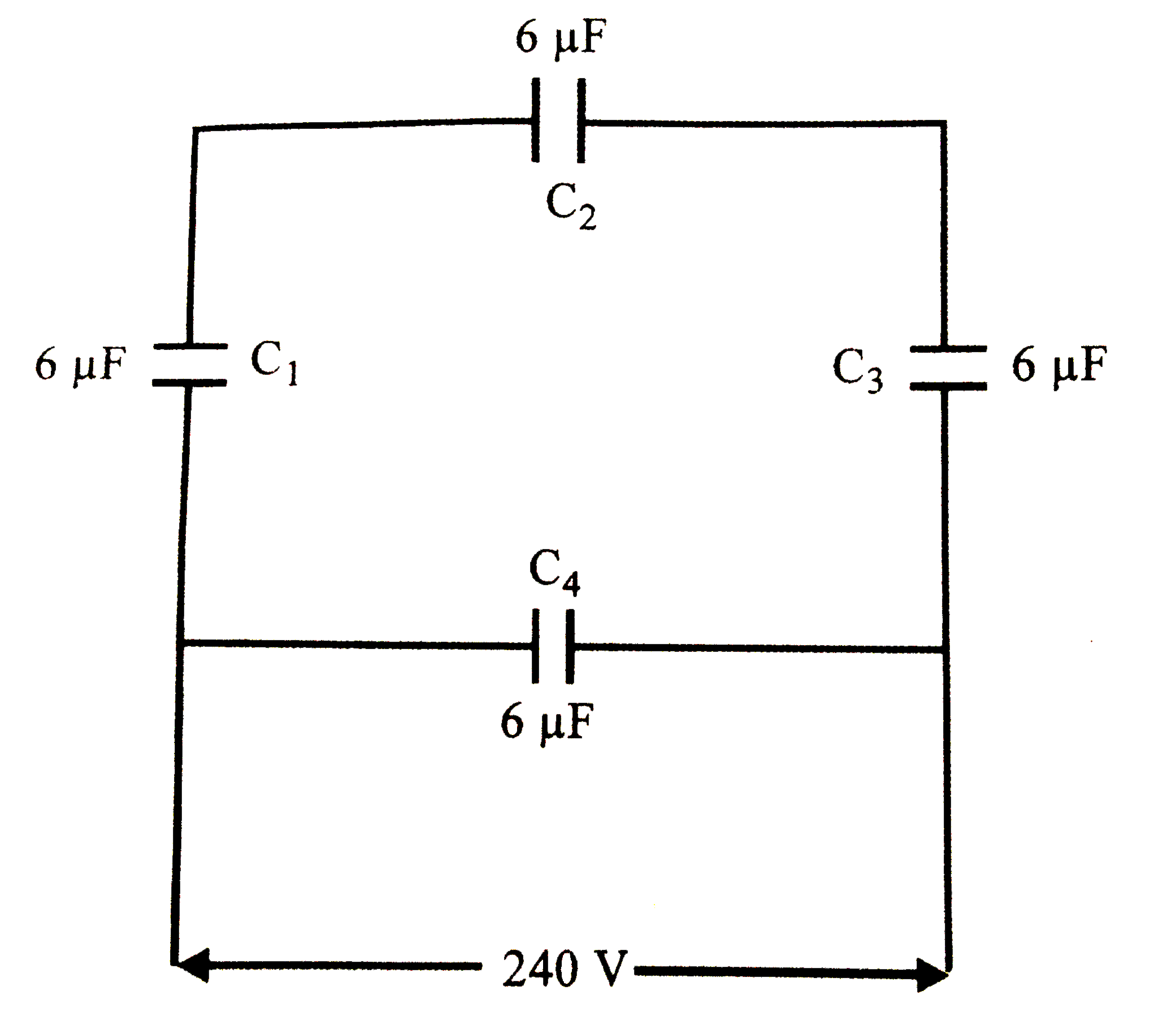
View SolutionA network of four capacitors of 6 μF each is connected to a 240 V supply. Determine the charge on each capacitor.
View SolutionIn figure C1=C5=8.4μF and C2=C3=C4=4.2μF.The applied potential is Vab=220V
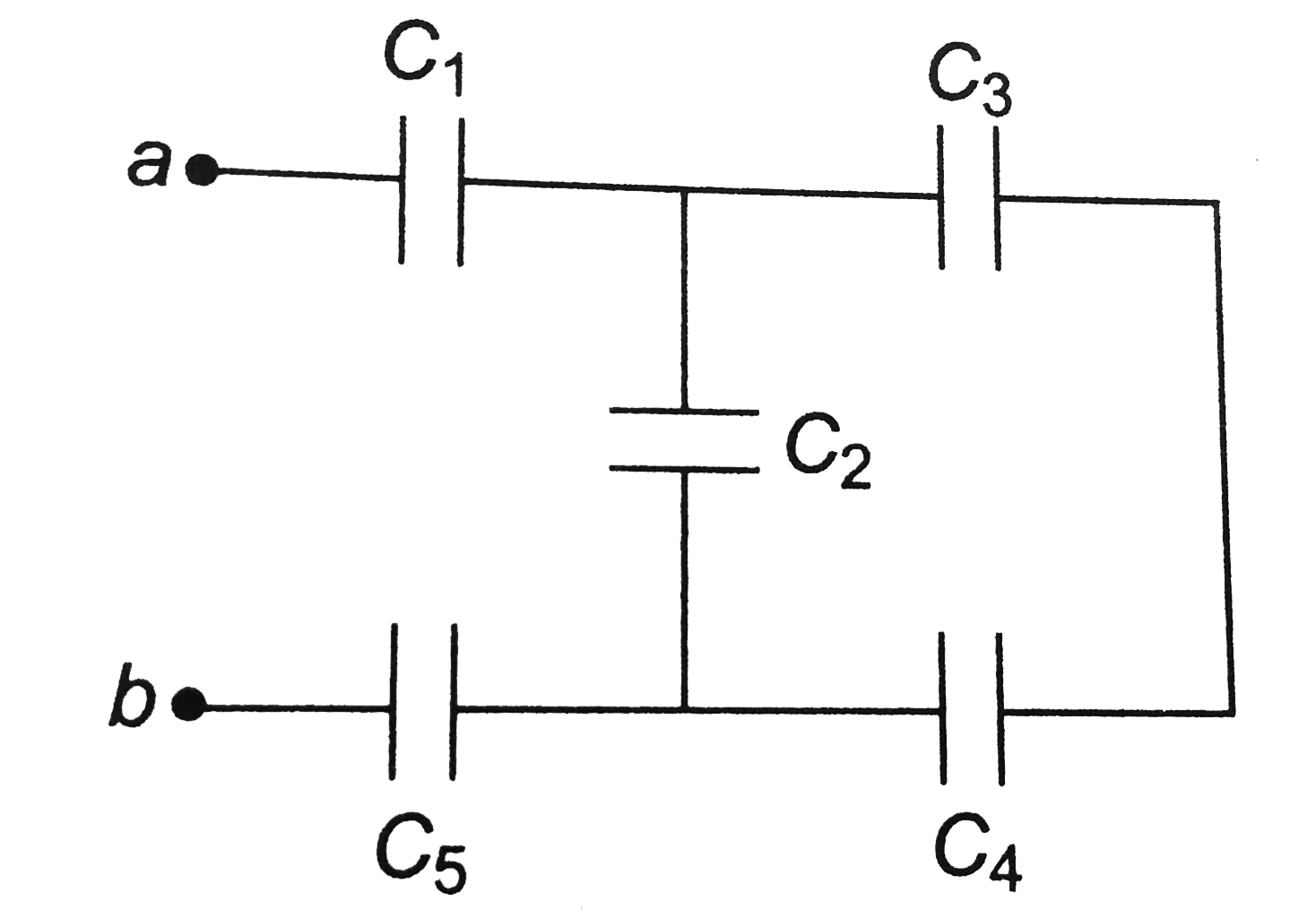
(a) What is the equivalent capacitance of the network between points a and b?
(b) Calculate the charge on each capacitor and the potential difference across each capacitor.
View SolutionFind the equivalent capacitance of the network shown in the fig , when each capacitor is of 1 μF . When the ends X and Y are connected to a 6 V battery , find out (i) the charge and (ii) the energy stored in the network

View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

View SolutionA 4.00μF capacitor and a 6.00μF capacitor are connected in parallel across a 660V supply line
(a) Find the charge on each capacitor and the voltage across each.
(b) The charged capacitors are disconnected from the line and from each other, and reconnected to each other with terminals of unlike sign together. Find the final charge on each and the voltage across each.
View SolutionA 1μF capacitor and a 2µF capacitor are connected in series across a 1200V supply line.
a. Find the charge on each capacitor and the voltage across them.
b. The charged capacitors are disconnected from the line and from each other and reconnected with terminals of like sign together. Find the final charge on each and the voltage across them.
View Solution

