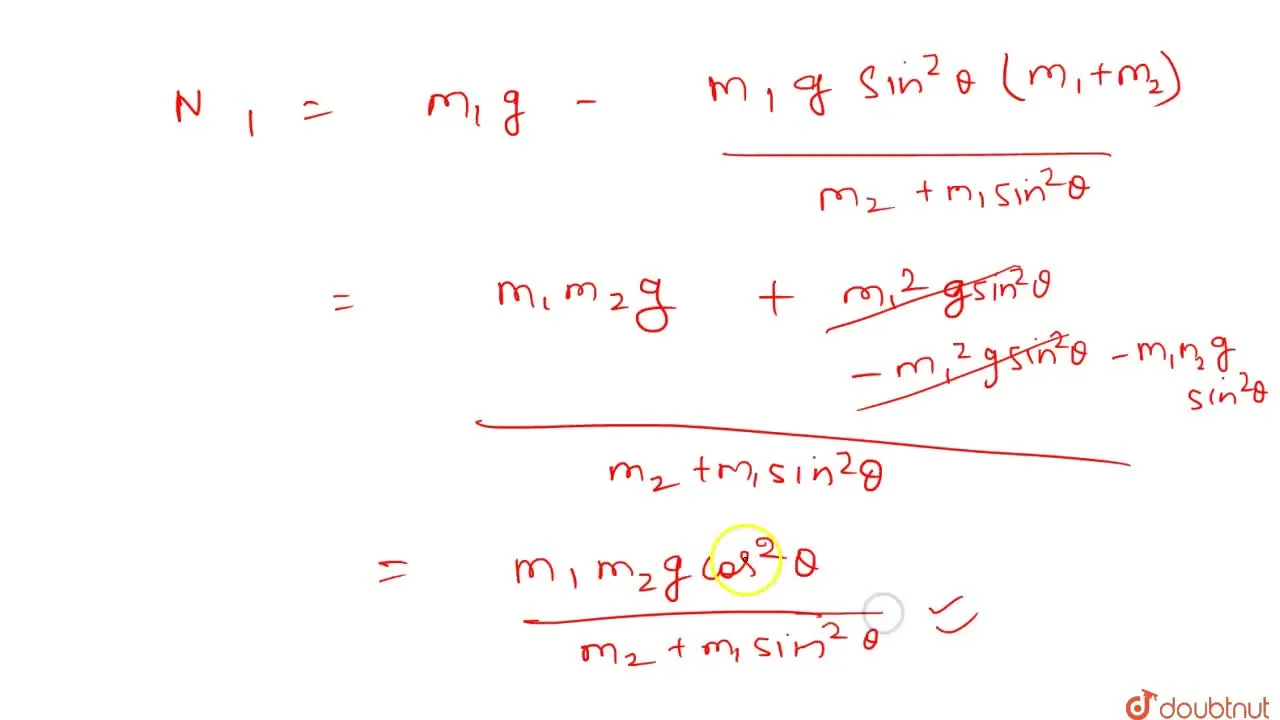Two blocks m1 and m2 are allowed to move without friction Block m1 is on block m2 and m2 slides on smooth fixed incline as shown The angle of inclination of inclined plane is θ
 .
.
Normal reaction on m1 is .
m1g
(m1+m2)g
m1m2gcos2θm2+m1sin2θ
m1g[1−(m1+m2)sin2θ]m1+m2sin2θ
The correct Answer is:C
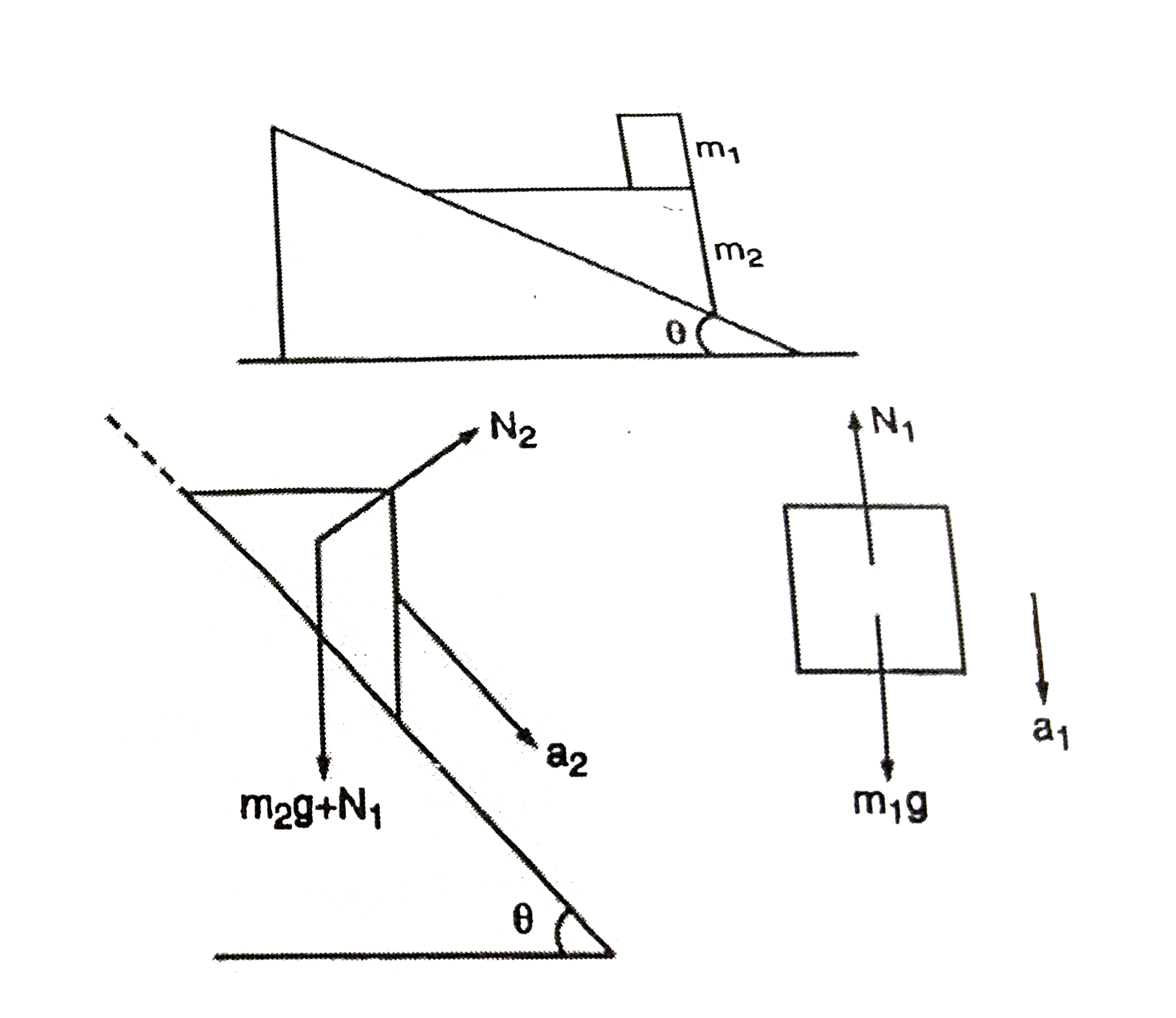
m1g−N1=m1a1 ….(i)
(N1+m2g)sinθ=m2a2 ….(ii)
From (i) and (ii)
[(m1g−m1a1)+m2g]sinθ=m2a2
(m1+m2)gsinθ−m1a1sinθ=m2a2 ....(iii)
Block m1 can move only in vertical direction as there is no force in horizontal direction. Since acceleration along normal at point of contact of the block and wedge should be equal.
So, a1=a2sinθ ...(iv)
Related Playlists
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Integer question15videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice35videos
BASIC MATHEMATICS
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
Similar Questions
Two blocks m1 and m2 are allowed to move without friction. Block m1 is on block m2 and m2 slides on smooth fixed incline as shown. The angle of inclination of inclined plane is θ
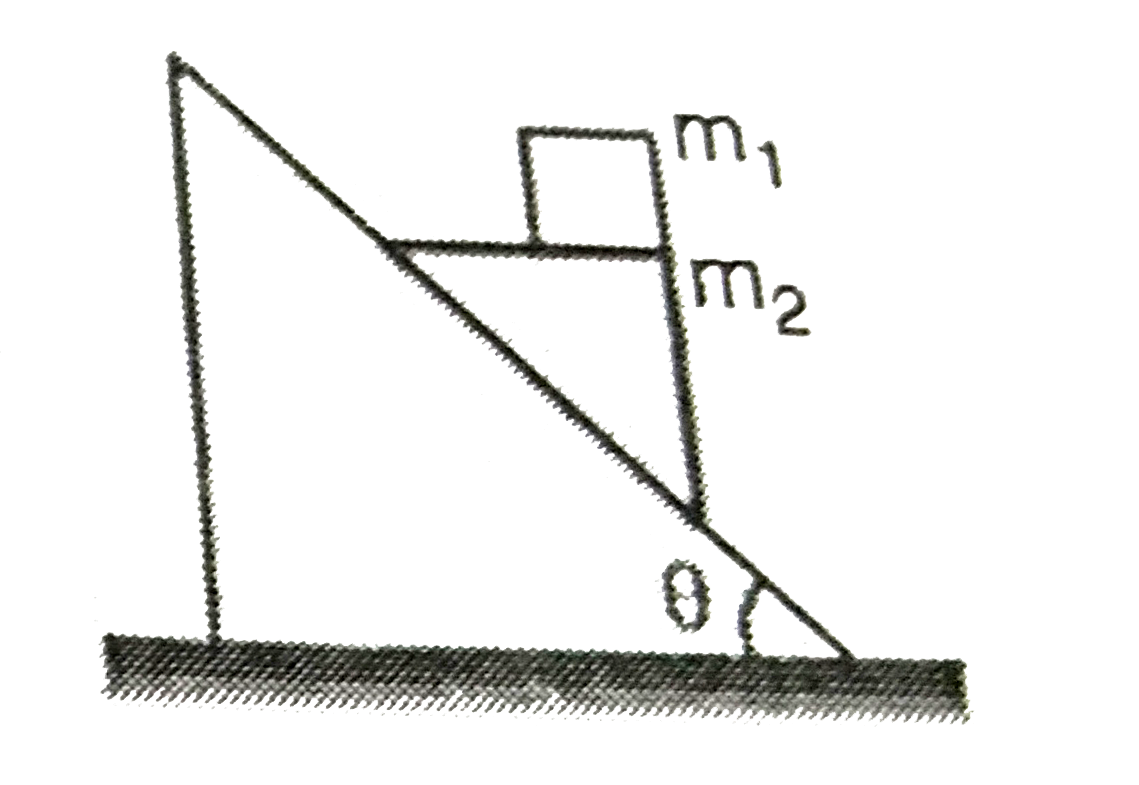
The acceleration of m1 with respect to ground is:View SolutionTwo blocks m1 and m2 are allowed to move without friction Block m1 is on block m2 and m2 slides on smooth fixed incline as shown The angle of inclination of inclined plane is θ
 .
.
The acceleration of m2 with respect to ground is .View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 View Solution
View SolutionBlock M slides down on frictionless incline as shown. The minimum friction coefficient so that m does not slide with respect to M would be :
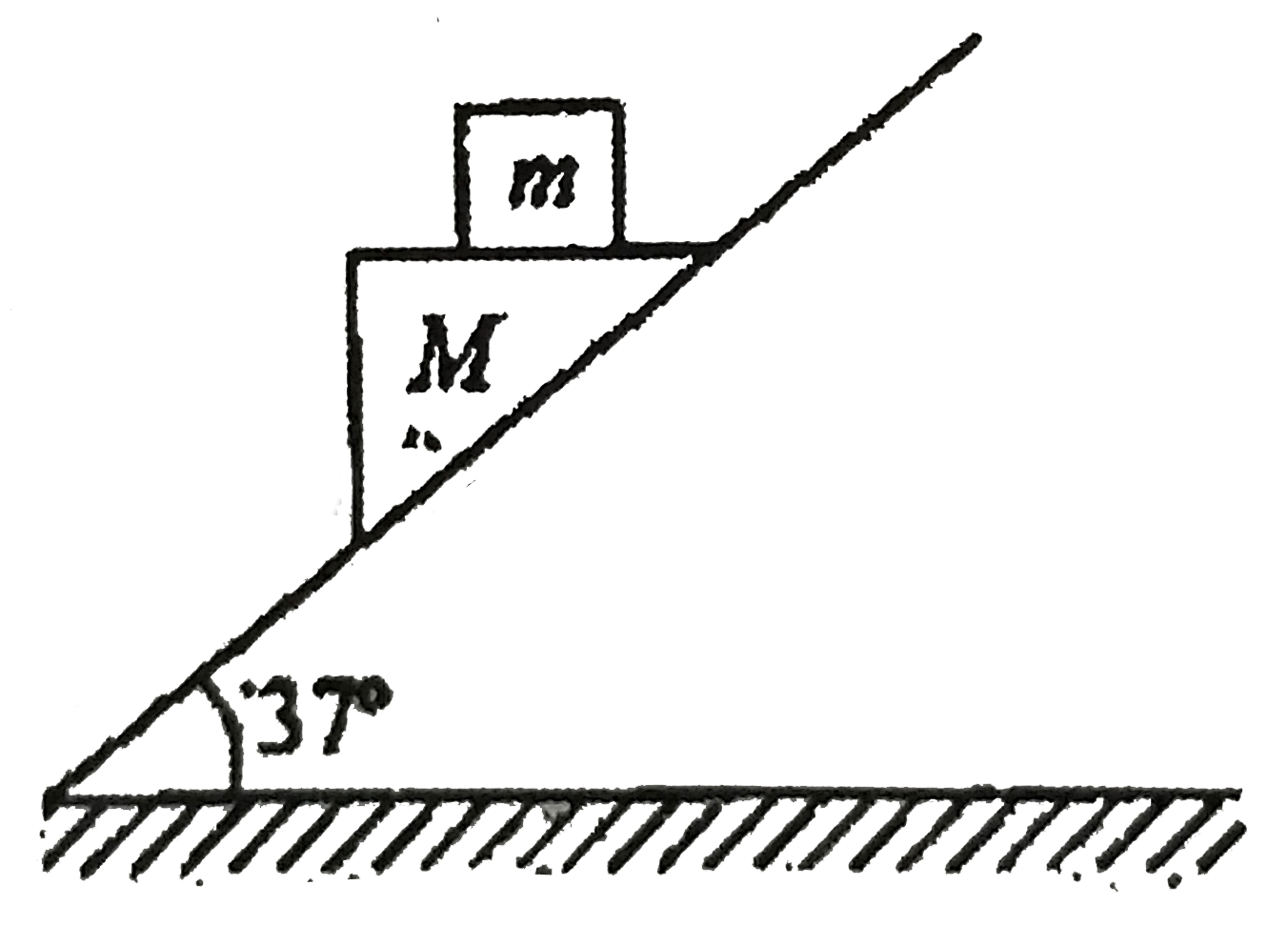 View Solution
View SolutionA block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
View SolutionA block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block
 View Solution
View SolutionThree blocks are placed at rest on a smooth inclined plane with force acting on m1 parallel to the inclined plane. Find the contact force between m2 and m3
 View Solution
View SolutionThree blocks are placed at rest on a smooth inclined plane with force acting on m1 parallel to the inclined plane. Find the contact force between m2 and m3
 View Solution
View SolutionA block can slide on a smooth inclined plane of inclination θ kept on the floor of a lift. When the lift is descending with a retardation a , the acceleration of the block relative to the incline is
View Solution