In fig Block $m_{2}$ is loaded on block $m_{1}$ . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

Video Solution

Text Solution

Verified by Experts

Assuming no friction between the surfaces,acceleration of block(1).
$a_{1} = \frac{m_{1} g sin θ}{m_{1}} = g sin θ$

and acceleration of block (2).
$a_{2} = \frac{m_{2} g sin θ}{m_{2}} = g sin θ$
Value of $| {¯ a}_{1} - {¯ a}_{2} | = | 1 g sin θ - g sin θ | = 0$
Here we can there is no tendency of relative sliding . Hence , no friction is present between (1) and (2).

Updated on:21/07/2023

A block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
A2 kg
B4 kg
C1.6 kg
D2.5 kg
If coefficient of friction between both the block is $μ - \frac{1}{2}$ . Find friction force acting between both block.

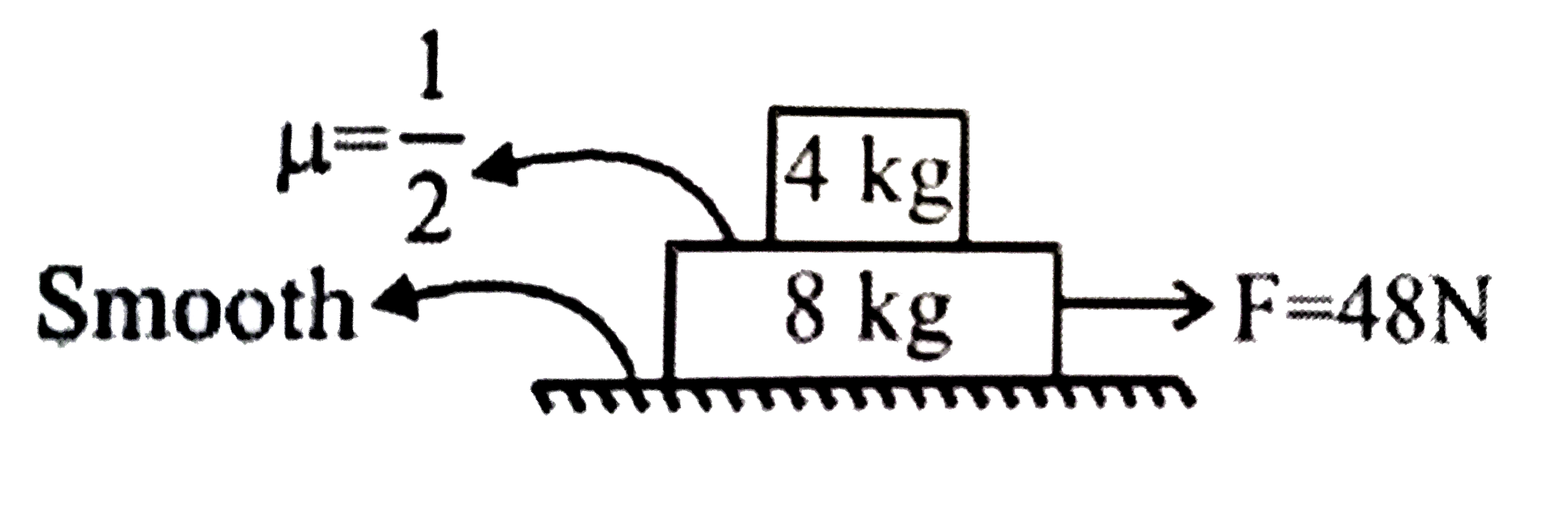A $16 N$
B $20 N$
C $8 N$
D $10 N$
A block of mass m slides down an inclined plane of inclination $θ$ with uniform speed. The coefficient of friction between the block and the plane is $μ$ . The contact force between the block and the plane is
Amg
B $m g sin θ \sqrt{1 + μ^{2}}$
C $m g sin θ$
D $\sqrt{{(m g sin θ)}^{2} + {(μ m g cos θ)}^{2}}$