A body starting from rest slides on an inclined plane of lengths as shown in Calculate the time of descent and speed at the bottom. Find also
(a) distance covered in half the time of descent and
(b) time taken to cover half the distance
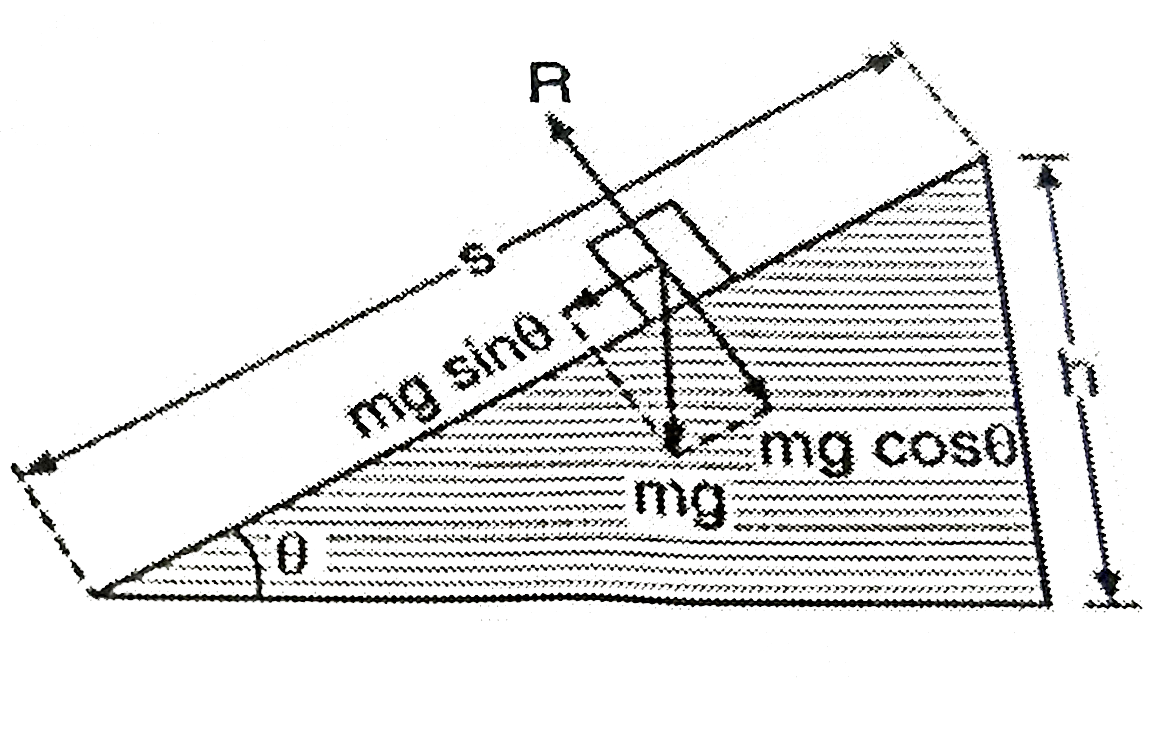
When a body slides on an inclined plane, component of weight along the plane produces acceleration
a=mgsinθm=gsinθ=constant
So, equations of motion can be applied, From 2 nd equation of motion, here
s=0+12(gsinθ)t2[asu=0] ....(i)
i.e, t=√2sgsinθ=1sinθ√2hg[as s=hsinθ].....(ii)
Whiel from 3 rd equation of motion,
v2=02+2(gsinθ)s
or v=√2gs(sinθ)=√2gh[as ssinθ=h] ...(iii)
Eqns (ii) and (iii) are the desired result. Further as from Eqn, (i) s∝t2 , so
(a) if t'=t2s's=(t/2t)2,i.e s'=s4
i.e, in half the time of descent the body covers only one fourth of the total distance
(b) ifs'=s2'(s/2s)=(t't)2,i.e t'=t√2≅0.7t
i.e, in about 0.7 times the time of descent the body covers half of the total distance.
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Problem for practice
Explore 30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Objective Questions
Explore 134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- BASIC MATHEMATICSBook:GRB PUBLICATIONChapter:BASIC MATHEMATICSExercise:Problems For Practice
Explore 35 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
Similar Questions
Knowledge Check
A body is dropped from a height H. The time taken to cover second half of the journey is
A2√2HgB√HgC√Hg(√2−1)D√2Hg×1(√2−1)A certain distance is covered at a certain speed. If half of this distance is covered i double the time , the ratio of the two speeds is
A0.16736111111111B0.044444444444444C0.084027777777778D0.043055555555556Starting from rest a body slides down a 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
A0.75B0.33C0.25D0.80
Ratio of speeds of A and B is a:b: then ratio of the time taken by them to cover the same distance
View SolutionAbhi covers a certain distance in 120 minutes. He covers half of the distance in 2/3 of the time.
Find the time taken to cover the remaining distance.
View SolutionKrishna covers a certain distance in 150 min. He covers half of the distance in 4/15 of the time. Find the time taken to cover the remining distance.
View SolutionA certain distance is covered at acertain speed. If half of this distance is covered in 4 times of the time,then find the ratio of the two speeds.
View SolutionA certain distance is covered at acertain speed. If half of the distance is covered in double time, the ratio of the two speeds is
View Solution

