Shots are fired simu ltaneou ly from the top and bottom of a vertical cliff at angles α and β and they stike an object simu ltaneously at the same point. If the horizontal distance of the object from the cliff is a, the height of the dcliff is :
a(cotα−cotβ)cotαcotβ
a(sinβ−tanα)
atanαtanβ
a(cotα−cotβ)
The correct Answer is:a
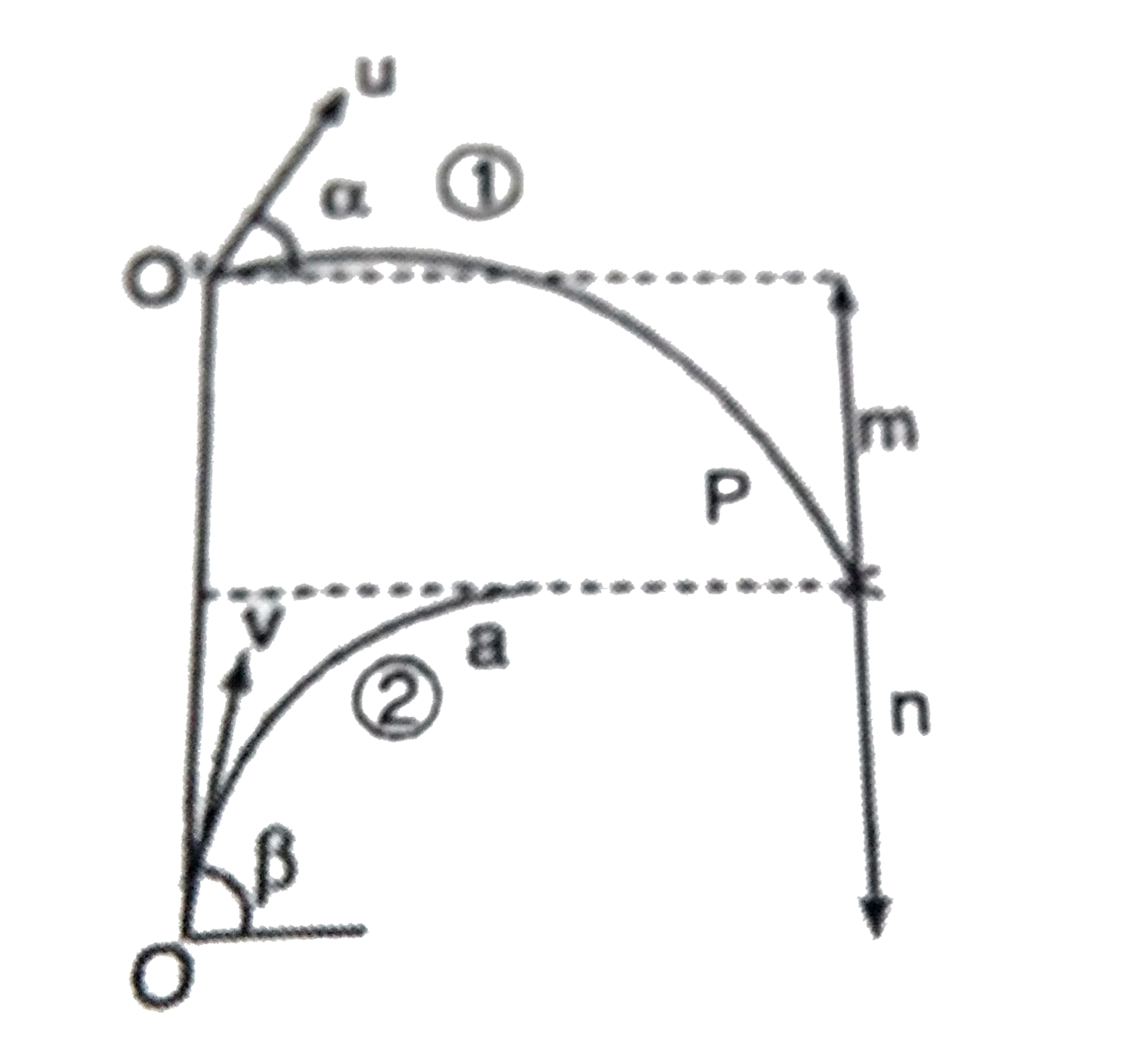
Coordinates of P w.r.t. O and O' as orgins are (a,n) and (a,-m). The height of the cliff =h=m+n.
y=xtanα−gx22u2cos2α
∴−m=atanα−ga22u2cos2α
v0=√2gh2+cot2θ,−n=atanβ−ga22v2cos2β
∴(m+n)=a(tanβ−tanα)
because ucosα=vcosβ because both the shots reach P simu ltaneously. This is possible only if the horizontal components of the velocities are equal.
Topper's Solved these Questions
Similar Questions
Shots are fired simultaneously from the top and bottom of a vertical cliff with elevation α and β respectively which strike an object simultaneously at the same point. If a is the horizontal distance of the object from the cliff, its height is ............
View SolutionShots are fired simultaneously from the top and the bottom of a vertical cliff with elevation 37∘ and 53∘ respectively, strike an object at the ground simultaneously.If the horizontal distance of the object from the cliff is 60m, find the height of the cliff.
View Solution
Knowledge Check
Shots are fired simultaneously from the top and bottom of a vertical cliff with the elevation α=30∘, beta =60∘, respectively. The shots strike an object simultaneously at the same point. If a=10(√3) m is the horizontal distance of the object from the cliff, then the height h of the cliff is
 A30 mB45 mC60 mD90 m
A30 mB45 mC60 mD90 mTwo projectiles are projected simultaneously from the top and bottom of a vertical tower of height h at angles 45∘ and 60∘ above horizontal respectively.Body strike at the same point on ground at distance 20m from the foot of the tower after same time.
The speed of projectile projected from the bottom isA40m/sB20√3m/sC40√3m/sD20√√3m/sAt 129 metre away from the foot of a cliff on level of ground , the angle of elevation of the top of the cliff is 30∘ . The height of this cliff is :
A50√3 metreB45√3 metreC43√3 metreD47√3 metre
A man on the deck of a ship 12 m above water level, observes that the angle of elevation of the top of a cliff is 60∘ and the angle of depression of the base of the is 30∘. Find the distance of the cliff from the ship and the height of the cliff. [use √3=1.732)
View SolutionThe top of a hill observed from the top and bottom of a building of height h is at angles of elevation αandβ. respectively. The height of the bill is
View SolutionThe top of a hill observed from the top and bottom of a building of height h is at angles of elevation αandβ. respectively. The height of the bill is
View SolutionTwo identical shells are fired from a point on the ground with same muzzle velocity at angle of elevation α=45∘ and β=tan−13 towards top of a cliff, 20m away from the point of firing. If both the shells reach the top simultaneously, then
height of the cliff is
View SolutionShots are fired from the top of a tower and from bottom simultaneously at angle 30∘ and 60∘ as shown. If horizontal distance of the point of collision is at a distance 'a' from the tower. Then height of tower h is
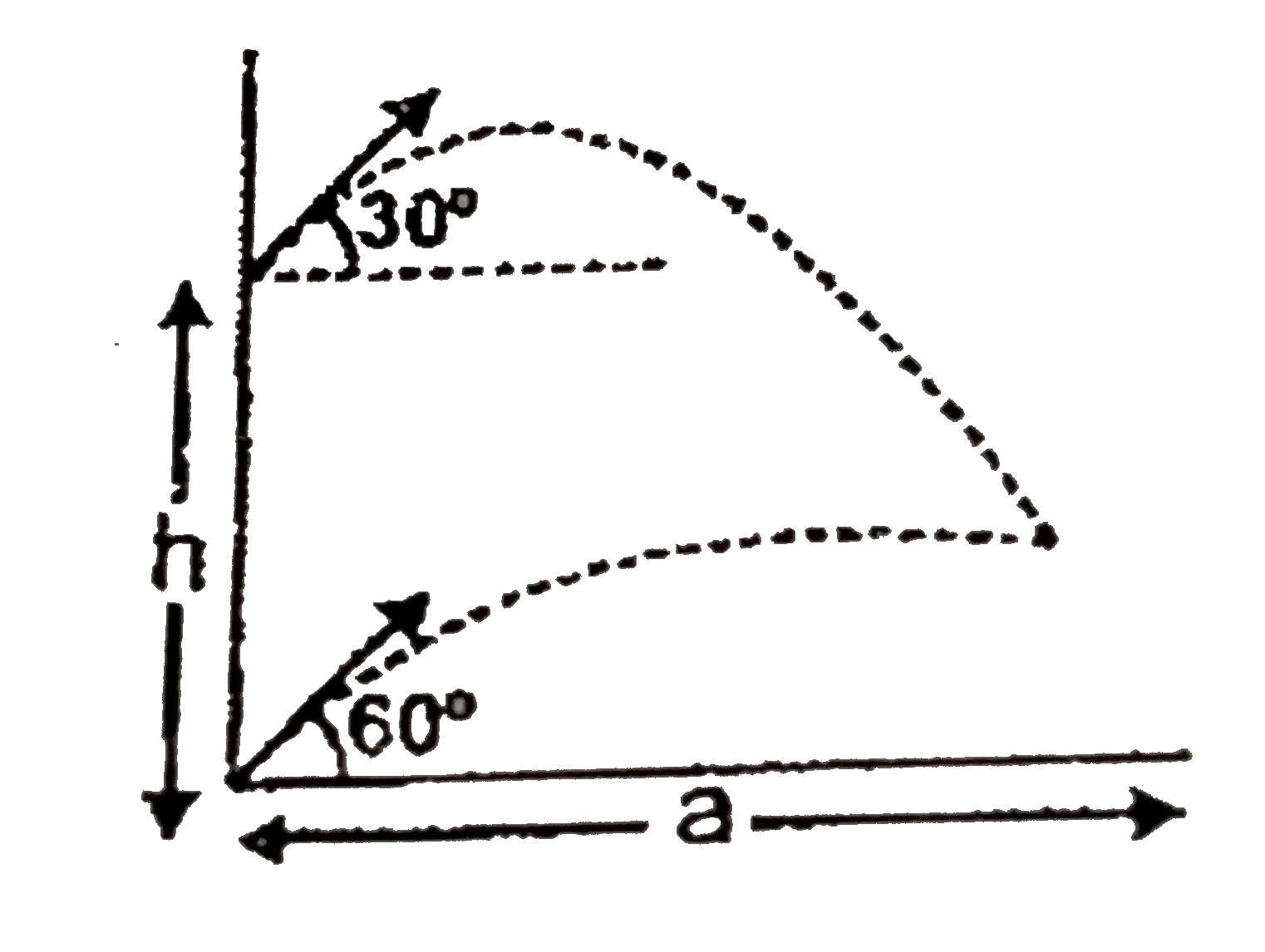
View Solution

