Shots are fired from the top of a tower and from bottom simultaneously at angle 30∘ and 60∘ as shown. If horizontal distance of the point of collision is at a distance 'a' from the tower. Then height of tower h is
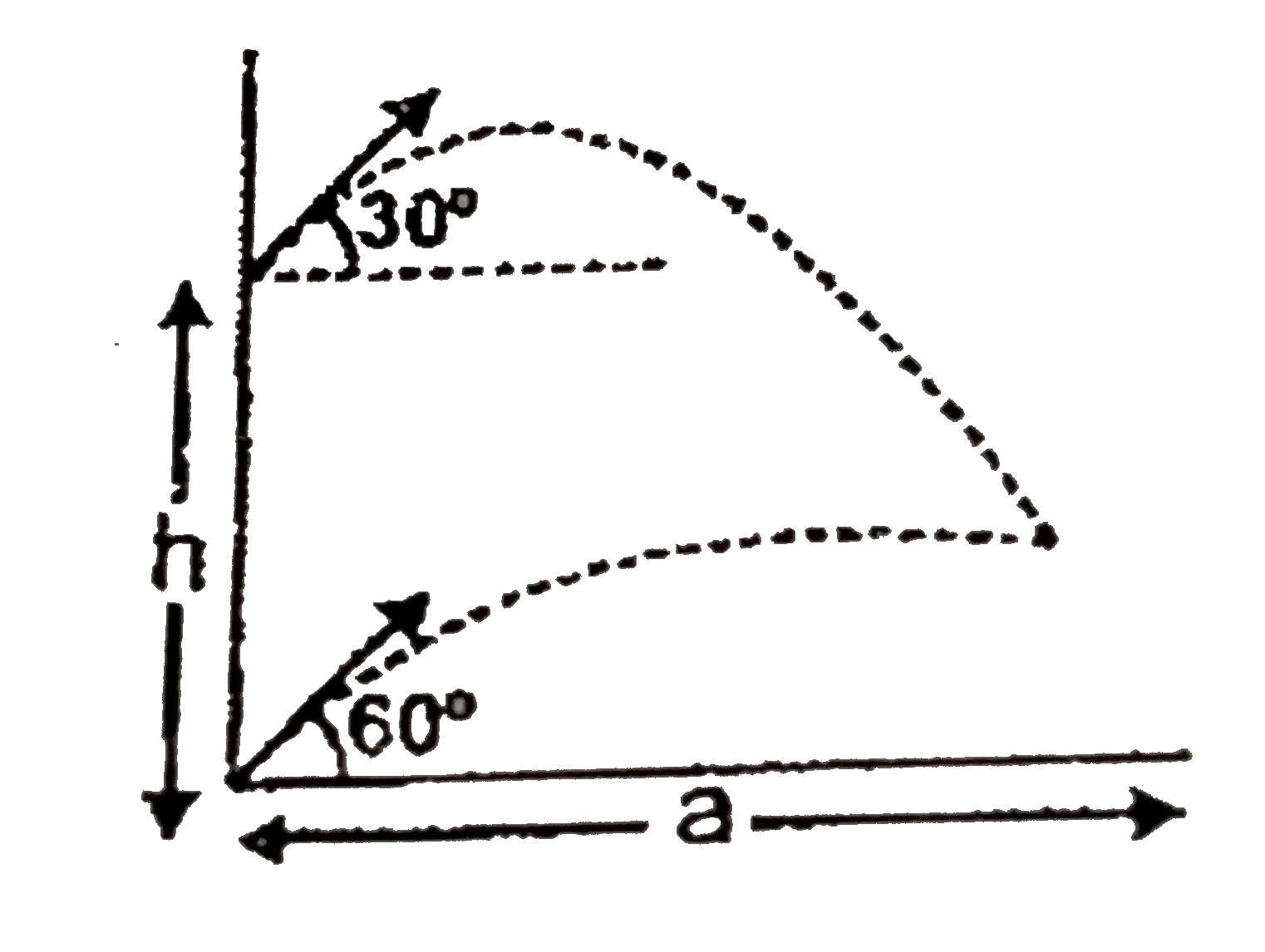
2a√3
a√3
2a
4a√3
The correct Answer is:A
For collision to take to place collision of velocity along x-should the same
∴ u1cos30∘ ⇒u2cos60∘
u1×√32 ⇒u2×12 ....(1)
Relative velocity along y-direction w.r.t upper ball-1
u⇒(u2sin60∘−u1sin30∘)
a = 0
s implies +h
t⇒hu2√32−u112⇒2h√3u2−u1
time should be same for both direction.
au2cos60∘=2h√3u2−u2√3
Solving this
2a⇒2h√32
h⇒2a√3

Topper's Solved these Questions
Similar Questions
The angle of elevation of the top of a tower from top of a house is60∘ and the angle of depresion of its base is 30∘. If the horizontal distance between the house and the tower is 12 m, then the hight of the tower is
View SolutionForm the top of a tower, the angle of depression of a point on the ground is 60∘. If the distance of this point from the tower is 1√3+1 m, then the height of the tower is
View Solution
Knowledge Check
The angle of depression of a point situated at a distance of 70 m from the base of a tower is 60∘.The height of the tower is :
A25√3mB70√3mC70√33mD70 mTwo projectiles are projected simultaneously from the top and bottom of a vertical tower of height h at angles 45∘ and 60∘ above horizontal respectively.Body strike at the same point on ground at distance 20m from the foot of the tower after same time.
The speed of projectile projected from the bottom isA40m/sB20√3m/sC40√3m/sD20√√3m/sFrom the top of a building of height h, a tower standing on the ground is observed to make an angle θ. If the horizontal distance between the building and the tower is h, the height of the tower is
A2hcosθsinθ+cosθB2h1+cotθC2h1+tanθD2hsinθ+cosθ
The angles of elevation of e top of an inaccessible tower from two points on the same straight line from the base of the tower are 30∘and60∘, respectively. If the points are separated at a distance of 100 m, then the height of the tower is close to
View SolutionThe angles of elevation of the top of a tower at two points, which are at distances a and b from the foot in the same horizontal line and on the same side of the tower, are complementary. The height of the tower is
View SolutionThe angle of elevation of the top of a tower from the top and bottom of a building of height 'a' are 30∘ and 45∘ respectively. If the tower and the building stand at the same level , the height of the tower is
View SolutionAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
View SolutionThe angle of elevation of top of a tower from a point on the ground is 30∘ and it is 60∘ when it is viewed from a point located 40 m away from the initial point towards the tower the height of the tower is
View Solution

