A particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is
12kt2
12at2
16at2
kt3
The correct Answer is:C
a=kt⇒dvdt=kt
∫dv=∫ktdt
v=kt22⇒dxdt=kt22
∫dx=∫kt22dt
x=kt36=(kt)t26=16at2
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:More than one choice is correct
Explore 16 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Assertion Reason
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Problems and Practice
Explore 16 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:GRB PUBLICATIONChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:All Questions
Explore 210 Videos
Similar Questions
A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement d.
View SolutionThe acceleration of a particle, starting from rest, varies with time according to relation , a=−rω2sinomηt. Find the displacemnt of this particle at a time (t).
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A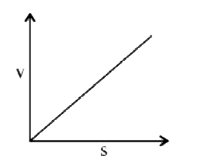 B
B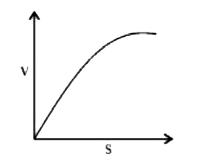 C
C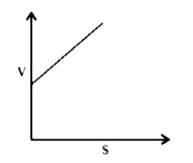 D
D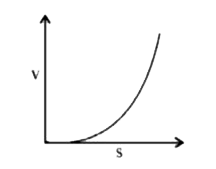
A particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Total force on particle at time t s isAm√k(R2+kt4)Bm√k(R+kt4)C2m√k(R+kt4)Dm2√k(R+kt4)A particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
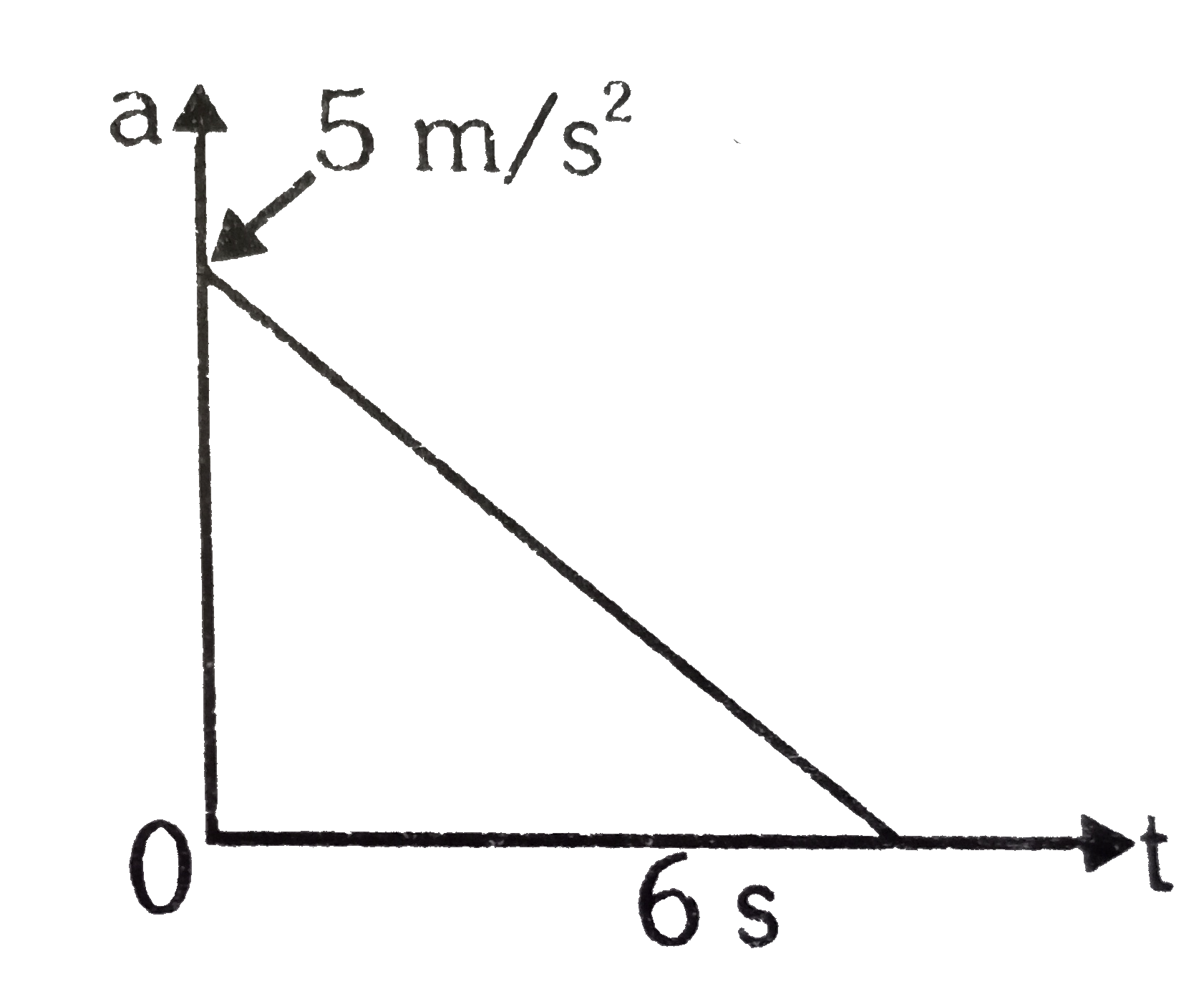 A7.5m/sB15m/sC30m/sD37.5 m/s
A7.5m/sB15m/sC30m/sD37.5 m/s
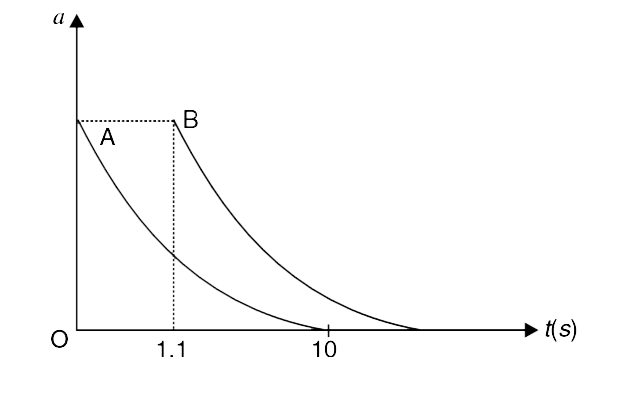
Particle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Tangential force on particle at t s is
View SolutionA particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Power developed by total at time t is
View SolutionA particle starts from rest and has velocity kt after time t. The distance travelled in time t is-
View Solution

