The speed of a body moving on a straight track varies according to and . The distance are measured in metre. The distance in metres moved by the particle at the end of 10 second is :
127
247
186
313
The correct Answer is:B
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:More than one choice is correct
Explore 16 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Assertion Reason
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Problems and Practice
Explore 16 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:GRB PUBLICATIONChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:All Questions
Explore 210 Videos
Similar Questions
The speed of a body moving on a straight trach varies according to v=45t2+3 for 0<t<5 sec and v=3t+8 for t>5 sec. If dinstances are in meters, find the distance moved by a particle at the end of 10 sec.
View Solution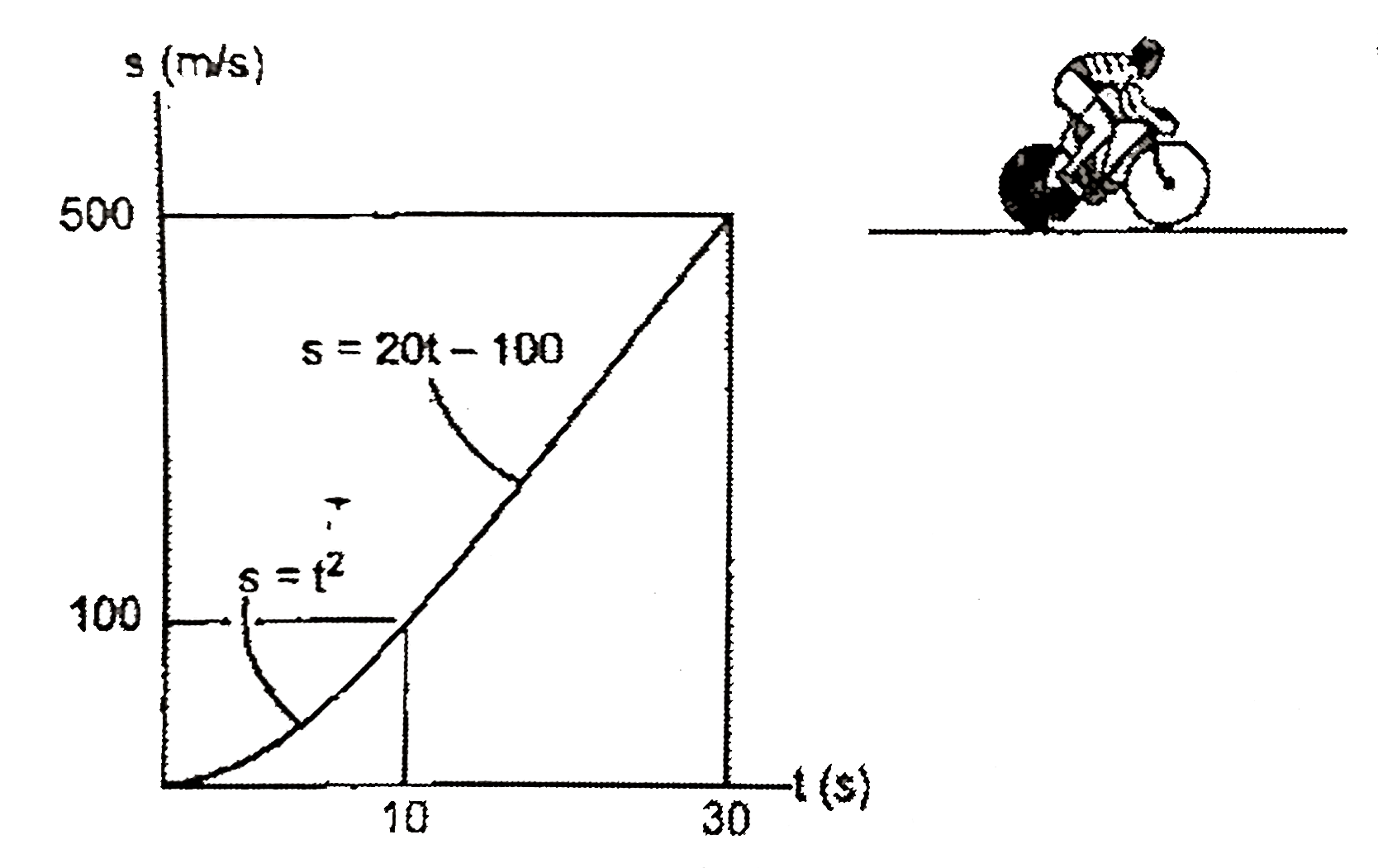
A bicycle moves along a stragith road such that its construct the v-t and a-t graphs for 0≤t≤30.
View Solution
Knowledge Check
The velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
A0B2 sC3DBoth (1) & (2)Velocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
A12mB16mC4mD8mThe distance travelled s in metres by a particle in t second is given by s=t3+2t2+t. The speed of the particle after 1s will be
A8cms−1B6cms−1C2cms−1DNone of these
The distance covered by an object (in meter) is given by
s=8t3−7t2+5t
Find its speed at t = 2 s.
View SolutionA particle starts moving rectilinearly at time t=0 such that its velocity(v) changes with time (t) as per equation –
v=(t2–2t)m/s for 0<t<2s
=(–t2+6t–8)m/s for 2≤te4s
(a) Find the interval of time between t=0 and t=4s when particle is retarding.
(b) Find the maximum speed of the particle in the interval 0≤t≤4s.
View SolutionThe distance s metres covered by a boy in t second, is given by s=3t2−8t+5. The boy will stop after
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
View Solution

