The speed of a body moving on a straight trach varies according to v=45t2+3 for 0<t<5 sec and v=3t+8 for t>5 sec. If dinstances are in meters, find the distance moved by a particle at the end of 10 sec.
The correct Answer is:(1453+3052)m
dsdt=45t2+3
⇒S1=∫S10ds=∫50(45t2+3)dt
S1=[415t3+3t]50=1453m
S2=∫S20ds=∫105(3t+8)dt
S2=[3t22+8t]105=3052m
S=S1+S2=(1453+3052)m
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - single correct type
14 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
If velocity is depend on time such that v = 4 – 2t. Find out distance travelled by particle from 1 to 3 sec
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View Solution
Knowledge Check
The speed of a body moving on a straight track varies according to v=2t+13 for 0≤t≤5s,v=3t+8 for 5<t<7s and v=4t+1 for t<7s. The distance are measured in metre. The distance in metres moved by the particle at the end of 10 second is :
A127B247C186D313In the given v-t graph, the distance travelled by the body in 5 sec will be :
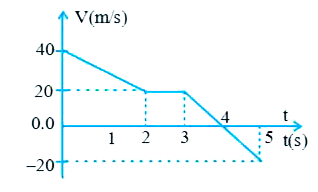 A100 mB80 mC40 mD20 m
A100 mB80 mC40 mD20 mA particle moves along a straight line according to the law s=16−2t+3t3 where s metres is the distance of the particle from a fixed point at the end of t sec the acceleration of the particle at the end of 2s is
A36ms2B34ms2C36mDnone of these
Velocity of a particle moving on straight line varies as v=2x ; where "x>0" and at "t=1" sec ",x=2m" its velocity at "t=4" sec is found n4 m/s Find "n
View SolutionThe initial velocity of the particle is 10m/sec and its retardation is 2m/sec2. The distance moved by the particle in 5th second of its motion is
View SolutionA particle is moving on a straight line with velocity (v) as a function of time (t) according to relation v=(5t2−3t+2)m/s . Now give the answer of following questions :
Acceleration of particle at the end of 3rd second of motion is :
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View Solution