![Find the area under the curve y=cosx over the interval (a) [0,(pi)/(2)] (b) [0,pi]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_DPP01_DPP2.7_E01_186_Q01.png)
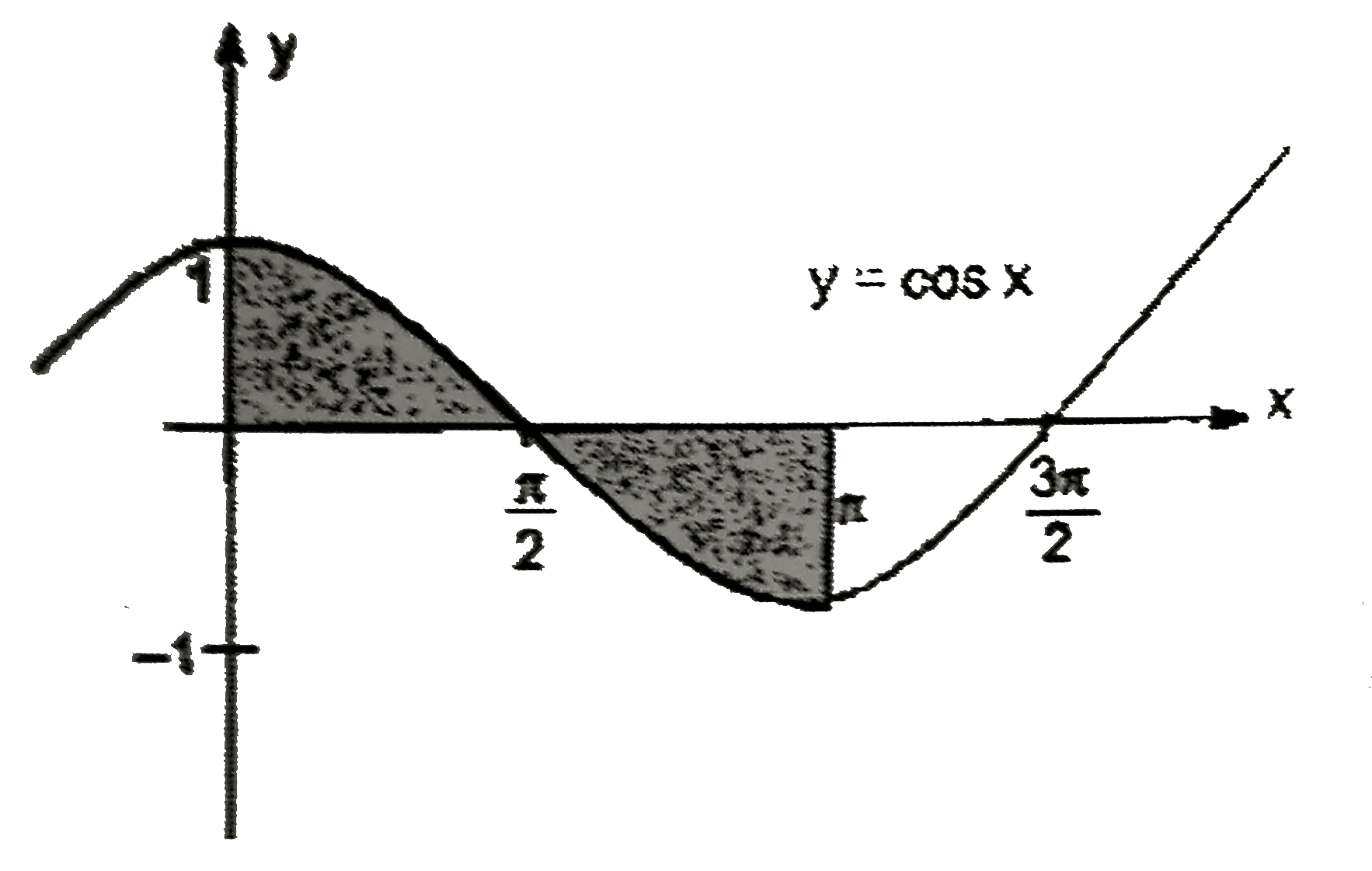
Find the area under the curve y=cosx over the interval
(a) [0,π2]
(b) [0,π]
Video Solution
Text Solution
(a). Since cosx≥0 over the interval [0,π2] the area A under the curve is
A=∫π20cosxdx=[sinx]π20=sin(π)2−sin0=1
(b). The given integral can be interpreted as the signed area between the graph of y=cosx and the interval [0,π]. The graph in figure suggests that over the interval [0,π] the portion of area above the x-axis is the same as the portion of area below the x-axis so we conjecture that the signed area is zero, this implies that the value of the integral is zero. This is confirmed by the computations.
∫π0cosxdx=sinx]π0=sinπ−sin0=0
|
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:single correct type
Explore 14 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICSChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBook:CENGAGE PHYSICSChapter:CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONExercise:Question Bank
Explore 38 Videos
Similar Questions
(a). Find the area under the curve y=cosx over the interval [0,π/2] and [0,π]
View SolutionFind the area bounded by the curve y=sin−1x and the line x=0,|y|=π2.
View SolutionFind the area bounded by the curve y=x sins-axis in the interval 0≤x≤2π.
View SolutionFind the average ordinate of the sinusoid y=sinx over the interval [0,π]
View SolutionFind the area bounded by the curve y=cosxbetween x=0and x=2π.
View SolutionFind the area bounded by the curve y=cosx between x=0andx=2π
View SolutionFind the area bounded by the curve y = sinx , the lines x = 0 and x=π/2.
View SolutionFind the area bounded by the curve y=sinxbetweenx=0andx=2π.
View SolutionFind area under the curve y=sin 2x between the ordinates x=π2 and x=π.
View SolutionFind the area bounded by the curve y=sinx between x=0 and x=2π.
View Solution

