
A rod AB is moving on a fixed circle of radius R with constant velocity v as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distancex=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.

As a rod AB moves, the point P will always lie on the circle. Hence its velocity will be along the circle as shoen by VP is the figure. If the point P has to lie on the rod AB also then it should have component in x direction as V
VPsinθ=V⇒VP=Vcosecθ
Here cosθ=xR=1R.3R5=35
sinθ=45⇒cosecθ=54
⇒=VP=54V
(b) And angular velocity ω=VPR=5V4R
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:single correct type
Explore 14 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICSChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBook:CENGAGE PHYSICSChapter:CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONExercise:Question Bank
Explore 38 Videos
Similar Questions
A rod AB is moving on a fixed circle of radius R=5m with constant velocity v=4m/s as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from center of the circle. The velocity of the rodf is perpendicular to its lenght and the rod is always paraller to the diameter (CD)
Speed of point of intersection P is

View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
View Solution
Knowledge Check
Two points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction, separated by a distance r. Then the angular velocity of the rod is :
A3vrB4vrC5vrD2vrEnd A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate

the velocity of the CM of the rodA57v0 at tan−143 below horizontalB57v0 at tan−134 below horizontalC56v0 at tan−134 below horizontalD56v0 at tan−143 below horizontalThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
AI4BI2C2ID4I
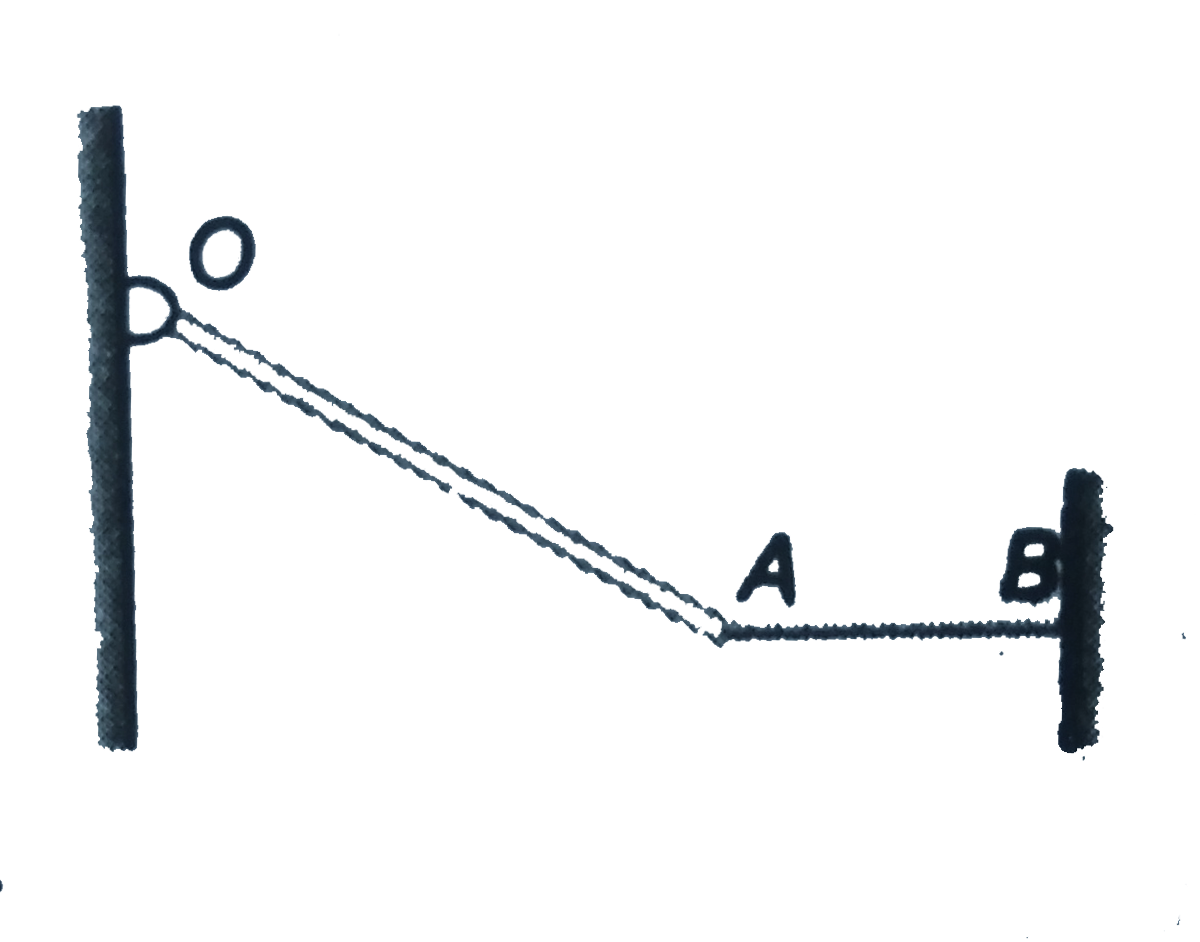
A rod OA is suspended with the help of a massless string AB as shown in figure. Rod is hinged at pointO. Draw free body diagrame of the rod.
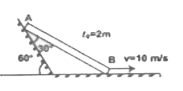
View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
View SolutionThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is

View Solution
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
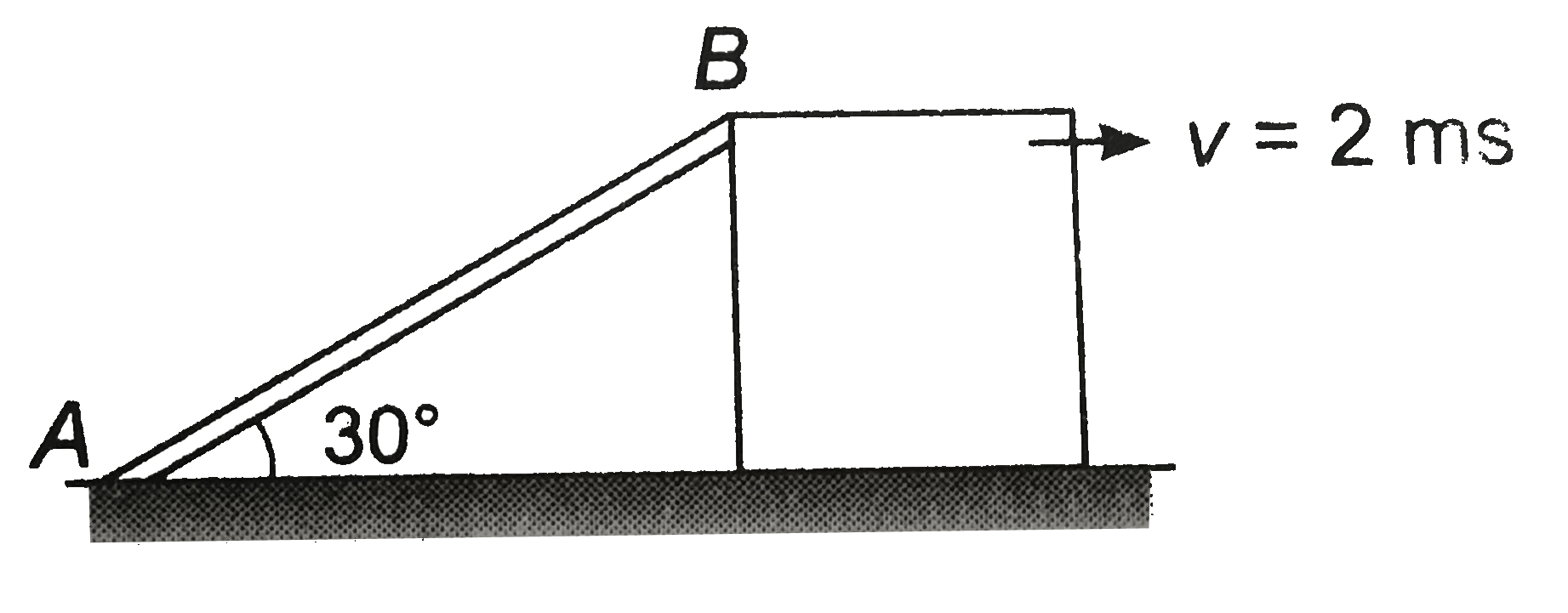
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
View Solution

