The block of mass m1 is placed on a wedge of an angle θ, as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is μ1, whereas it is μ2 between the wedge and the horizontal surface. if μ1=12,θ=45∘,m1=4kg,m2=5kg and g=10m/s2, find minimum value of μ2 so that the wedge remains stationary on the surface. express your answer in multiple of 10−3
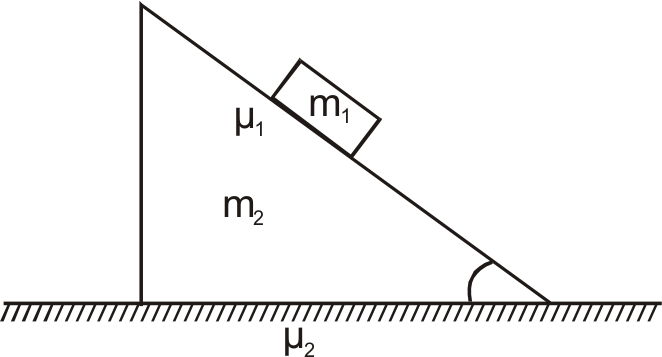


Taking block + wedge as system and applying NLM in horizontal direction
f2=m1acosθ
m1[g(sinθ−μ1cosθ]cosθ
Again applying NLM in vertical direction
(m1+m2)−N2=m1asinθ
N2=(m1+m2)g−m1sinθ(gsinθ−μ1gcosθ)
For limiting condition
f2=μ2N2
From (1) and (2)
μ2=m1cosθ(gsinθ−μ1gcosθ)(m2+m2)g−m1sinθ(gsinθ−μ1gcosθ)
Using values μ2=18
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - single correct type
14 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
Knowledge Check
a Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
 Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
A(M+m)gB(M+msinθ)gCMgD(M+msinθM+m)gcosθA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
 A0.1B0.2C0.3D1√2
A0.1B0.2C0.3D1√2
Two blocks of mass m and 2m are arranged on a wedge that is fixedd on a horizontal surface. Friction coefficient between the block and wedge are shown . Find the magnitude of acceleration of two blocks.

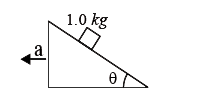
View SolutionA block of mass 1.0 kg rests on a wedge of angle θ. The acceleration which should be given to the wedge so that the block falls freely is :
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionIn the figure if block A and wedge b will move with same acceleration, then the magnitude of normal reaction between the block and the wedge will be (There is no friction between block and the wedge and the wedge moves on horizontal surface as shown.)
View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.

View Solution
