The acceleration of a particle, starting from rest, varies with time according to relation , a=−rω2sinomηt. Find the displacemnt of this particle at a time (t).
Acceleration, a=dvdt=−rωsinωt.
or dv=−rω2sinωdt,
Integratine it we have
v=−rω2(−cosωtomη)=rcosωt.
Now, velocity v=dxdt=rωcosωt
or dx=romηcosωtdt
Integrating it, we have
x=rω(sinωtω)=rsinωt.
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:3 Short answer
Explore 37 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 Short answer
Explore 30 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 Short answer
Explore 25 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
The acceleration a of a particle starting from rest varies with time according to relation, a=αt+β. Find the velocity of the particle at time instant t.
Strategy : a=dvdt
View SolutionThe acceleration of a particle varies with time t seconds according to the relation a=6t+6ms−2. Find velocity and position as funcitons of time. It is given that the particle starts from origin at t=0 with velocity 2ms−1.
View Solution
Knowledge Check
The acceleration of a particle starting from rest, varies with time according to the relationA=−aωsinmegat.. The displacement of this particle at a time t will be
A−12(aω2sinωt)t2BaωsinωtCaωcosωtDasinωtω−atThe acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c. The velocity of the particle after time t will be :
Akt2+ctB1.2kt2+ctC12(kt2+ct)Dkt2+12ctThe acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be
A2t3+3Bt2+3tC2t2+3tDzero
The acceleration of particle varies with time as shown.
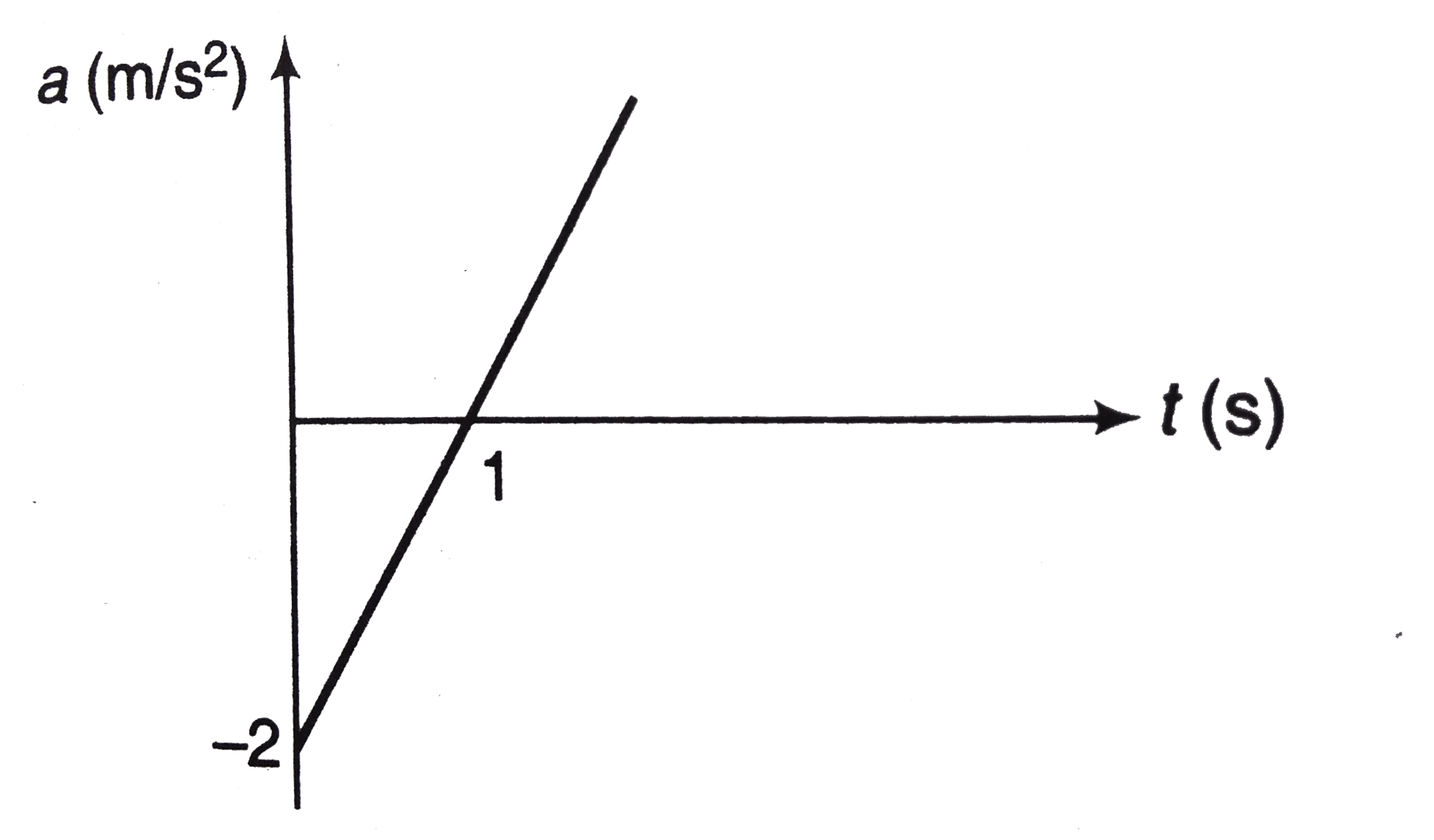
(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View SolutionThe displacement of a particle varies with time according to the relation y=asinωt+bcosωt.
View SolutionA particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is
View SolutionThe acceleration of a particle, given by relation, a=−5ω2sin(ωt). At t=0, x=0 and v=5ω. The displacement of this paticle at time t will be
View SolutionA particle starts from rest with a time varying acceleration a=(2t−4). Here t is in second and a in m/s2
The velocity time graph of the particle is
View Solution

