The distance coverd by an object between times t1andt2 is given by the area under the v−t gaph between t1andt2 Prove this staement for an object moving with negative acceleration and gaving and having a positive velocity at time t1andand¬ativevelocityattimet_(2).
The velocity-time graph for the motion of object as per question is shown in Fig. 2 (b) . 28 . Let v1bethevelocityofobjectattime T_(1) and -v_(2) bethevelocityofobjectattime t_(2).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V01_C02_S01_387_S01.pngwh=80%mx-autosty≤=background:white;>.<br>Let(S)bethedistancetravel≤d∈betweentimings t_(1) and t_(2).LetCbeap∮onthestraightl∈e AB,wherethegraphcutsthetimeaξsand(t')bethetimecorrespond∈g→p∮ C.<br>Areaunderthe u-tgrapgbbetweentimingst_(1)andt_(2)is<br>A=area AA_1 C + area CBB_1<br>= 1/2 A_1 C xx AA_1 + 1/2 CB_1 xx BB_1<br>= 1/2 (t' -t') xx v-1 + 1/2 (_2 -t') xx (-v_2)<br>= 1/2 v_1 (t' -t_1) - 1/2 v-2 (t _2 - t')...(i)<br>Weknowtˆtheae≤ration(a)ofanobjectisequal→theslopeof v-tgraph.Tak∈gslopethe v-tgraphbetweemthep∮s A and C,wehave<br> a= (velocity at t'-velocity at t_1)/(t'-t_1)<br>= (o-v_1)/(t'-t') =- v_1/(t'-t_1) or t' -t =- v_1/a<br>Slopeof v-tgraphbetweenthep∮s B and C,wehave<br> a= (velocity at t'-velocity at t_')/(t_2-t')<br> = (-v_2)-0)/9t_2 -t' ) =- v_2/(t_2 -t') or t_2 -t' =- v_2/a<br>Πomgtjeva,ies∈(i),we≥t<br> A= 1/2 v_1 (- v_1/a) - 1/2 v_2 (- v_2/a)<br>=- v_1^2/(2 a) + v_2^2/(2 a) = (v_2^2-v_1^2)/92 a) = (2 a S) /(2 a) =S<br>Henceareaunder v-tgraphbetweentimings t_1 and t_2isequal→thedistancecoverdbyobjectbetweentimings t_1 and t-2.
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:3 Short answer
Explore 37 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 Short answer
Explore 30 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 Short answer
Explore 25 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
Knowledge Check
Velocity is given by v=4t(1−2t), then find time at which velocity is maximum
A0.25 sB1 sC0.45 sD4sThe distance (in metre)travelled by a vehicle in time t(in secods) is given by the equation s=3t3+2t2+t+1. The different in the acceleration between t=2 and t=4 is
A36m/s2B38m/s2C45m/s2D46m/s2The distance (in metre)travelled by a vehicle in time t(in secods) is given by the equation s=3t3+2t2+t+1. The different in the acceleration between t=2 and t=4 is
A36m/s2B38m/s2C45m/s2D46m/s2
A body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
View SolutionIf displacement S at time t is S=−t3+3t2+5, then velocity at time t=2 sec is
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionEach of the three graphs represents acceleration versus time for an object that already has a positive velocity at time t1. Which graphs show an object whose speed is increasing for the entire time interval between t1 and t2?

View SolutionEach of the three graphs represents acceleration versus time for an object that already has a positive velocity at time t1. Which graphs show an object whose speed is increasing for the entire time interval between t1andt2 ?
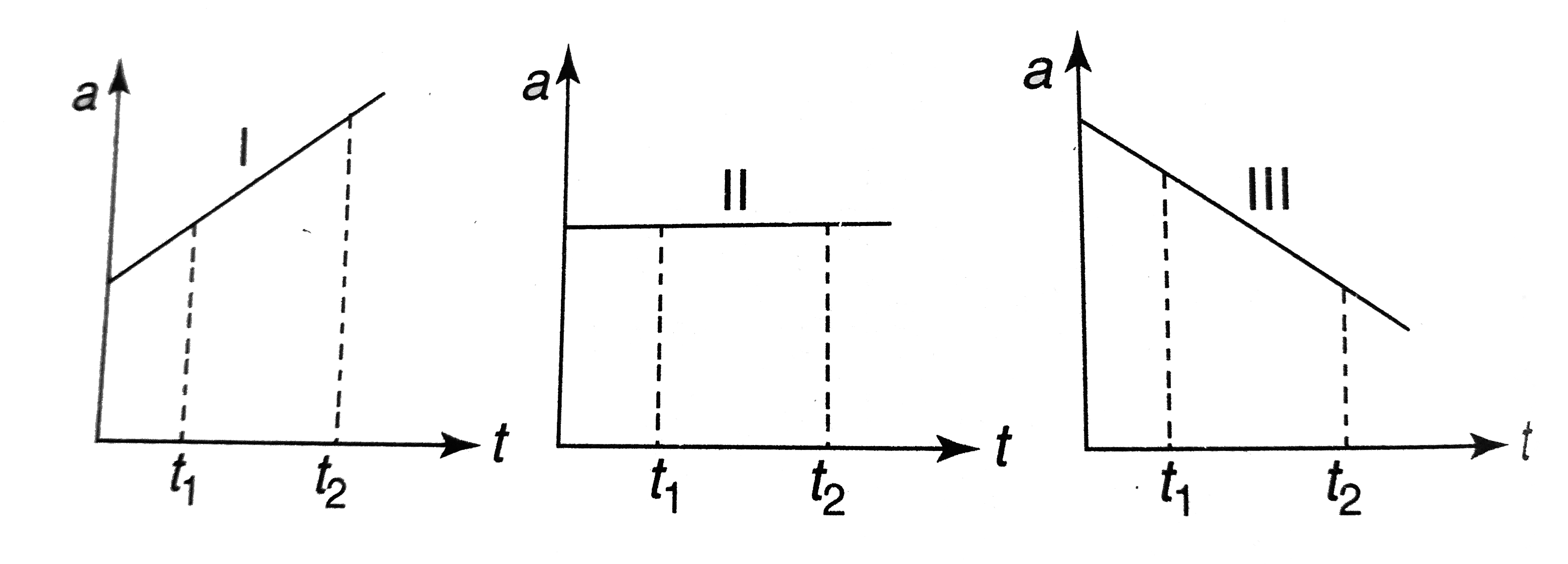
View Solution

