A boy swims in a straight line to reach the other side of a river. His velocity is 5 ms–1 with respect to water and the angle of swim with shore is 37∘. Flow of river opposes his movement at 2 ms–1. If width of river is 300 m, where does he reach the other bank.
200m from O' upstream
186 m from O' upstream
200m from O' downstream
186 m from O' downstream
The correct Answer is:A
Step by step video, text & image solution for A boy swims in a straight line to reach the other side of a river. His velocity is 5 ms^–1 with respect to water and the angle of swim with shore is 37^(@). Flow of river opposes his movement at 2 ms^–1. If width of river is 300 m, where does he reach the other bank. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 2 OBJECTIVE PROBLEMS (Level-2)
Explore 26 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 3 SUBJECTIVE PROBLEMS (Level-1)
Explore 20 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 1 OBJECTIVE PROBLEMS
Explore 103 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBook:MOTIONChapter:HYDROSTATIC, FLUID MECHANICS & VISCOSITYExercise:EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
Explore 7 Videos
- KINETIC THEORY OF GASES Book:MOTIONChapter:KINETIC THEORY OF GASES Exercise:EXERCISE-3 SECTION-B
Explore 16 Videos
Similar Questions
Width of a river is 30m, velocity is 2m/s and rowing velocity is 5m/s at 37∘ from the direction of river current find the time taken to cross the river.
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View Solution
Knowledge Check
A person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
A9.4B2C84.6D28.2A motor boat is to reach at a point 30∘ upstream on the outer side of a river flowing with velocity 5ms−1. The velocity of motor boat with respect to water is 5(√3)ms−1. The driver should steer the boat at an angle.
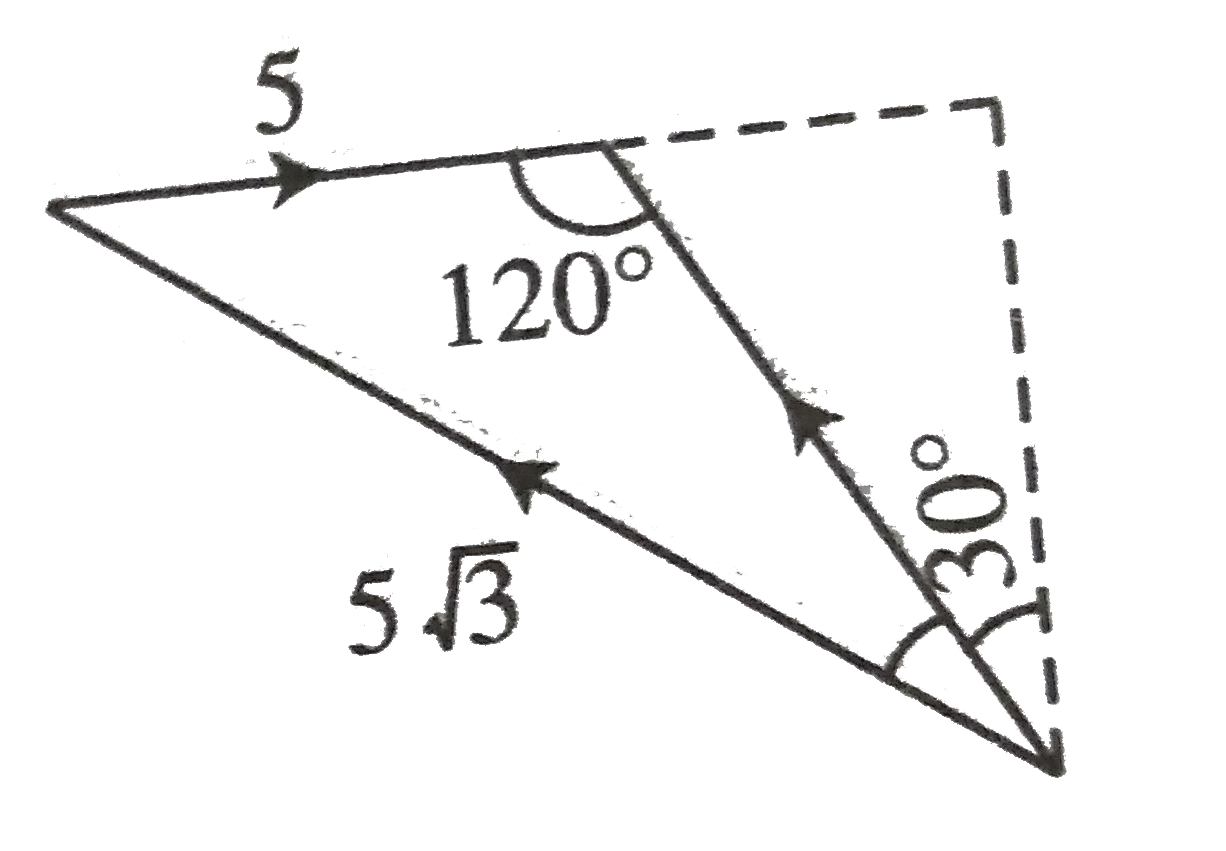 A30∘ w.r.t. the line of destination from the starting point.B60∘ w.r.t. normal to the bank.C120∘ w.r.t. stream directionDNone of these
A30∘ w.r.t. the line of destination from the starting point.B60∘ w.r.t. normal to the bank.C120∘ w.r.t. stream directionDNone of theseA man can swim with speed 5ms−1 in still river while the river is also flowing speed 10ms−1 If the width of the river is 100 m then minimum possible drift is
A100 mB0C100√3mD100√2m
A man can swim at a speed 2ms−1 in still water. He starts swimming in a river at an angle 150∘ with direction of flow of water and reaches at the exactly oppsite point on the opposite bank.
(a) Find the speed of flowing water.
(b) If width of river is 1 km then calculate the time taken also
View SolutionA man can swim with a speed 4km/hr in still water.
(a) How long does he takes to cross a river 1 km wide if the river flows steadily at 3 km/hr and makes his strokes normal to the river current?
(b) How far down the river does he go when he go when he reaches the other bank?
View SolutionA river 60m wide is flowing at a rate of 4m/s .A boat is sailing at a velocity of 20 m/s with respect to the river in a direction making an angle 37∘ with the direction of river flow.Find time taken by the boat in seconds to reach the opposite bank. (A) 2 (B) 3 (C) √6 (D) 5
View SolutionA swimmer wishes to reach directly opposite bank of a river, flowing with velocity 8 m/s. The swimmer can swim 10 m/s still water. The width of the river is 480 m. Time taken by him to do so:
View SolutionA man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
View Solution

