Four particles situated at the corners of a square of side ‘a’ move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.

A

$\frac{a}{v}$

B

$\frac{a}{2 v}$

C

$\frac{a}{3 v}$

D

$\frac{2 a}{3 v}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem of four particles situated at the corners of a square of side 'a' moving towards each other, we can follow these steps:
Step 1: Understand the Configuration
The four particles are located at the corners of a square. Let’s label the corners as A, B, C, and D. Each particle moves towards the next particle in a clockwise direction:
- Particle A moves towards Particle B
- Particle B moves towards Particle C
- Particle C moves towards Particle D
- Particle D moves towards Particle A
Step 2: Analyze the Motion
Since each particle is always moving towards the next particle, they will spiral inward towards the center of the square. The distance between any two adjacent particles (e.g., A and B) is initially 'a'.
Step 3: Determine the Relative Velocity
To find out how long it will take for the particles to meet, we need to consider the relative velocity of one particle towards another. For example, consider Particle A moving towards Particle B. The speed of Particle A is 'v', and since it is directed towards Particle B, we need to find the component of this velocity in the direction of the line joining A and B.
Step 4: Calculate the Time to Meet
1. The distance between A and B is 'a'.
2. The relative velocity of A towards B is 'v' because Particle A is moving directly towards Particle B.
3. The time taken $t$ for Particle A to meet Particle B can be calculated using the formula:
$t = \frac{Distance}{Relative Velocity} = \frac{a}{v}$
Step 5: Conclusion
Since all particles are moving towards each other in a similar manner, they will all meet at the same time. Therefore, the time taken for all four particles to meet at the center of the square is:
$t = \frac{a}{v}$
Final Answer
The time taken for the particles to meet each other is $\frac{a}{v}$ .
---

|

Updated on:7/8/2024

Class 12 PHYSICS KINEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Four particles of masses 1 kg, 2 kg, 3 kg, and 4 kg are situated at the corners of a square and moving at speed $3 m s^{- 1}, 4 m s^{- 1}, 1 m s^{- 1}$ and $2 m s^{- 1}$ respectively. Each particle maintains a direction towards the particle at the next comer symmetrically. The momentum of the system at this instant is

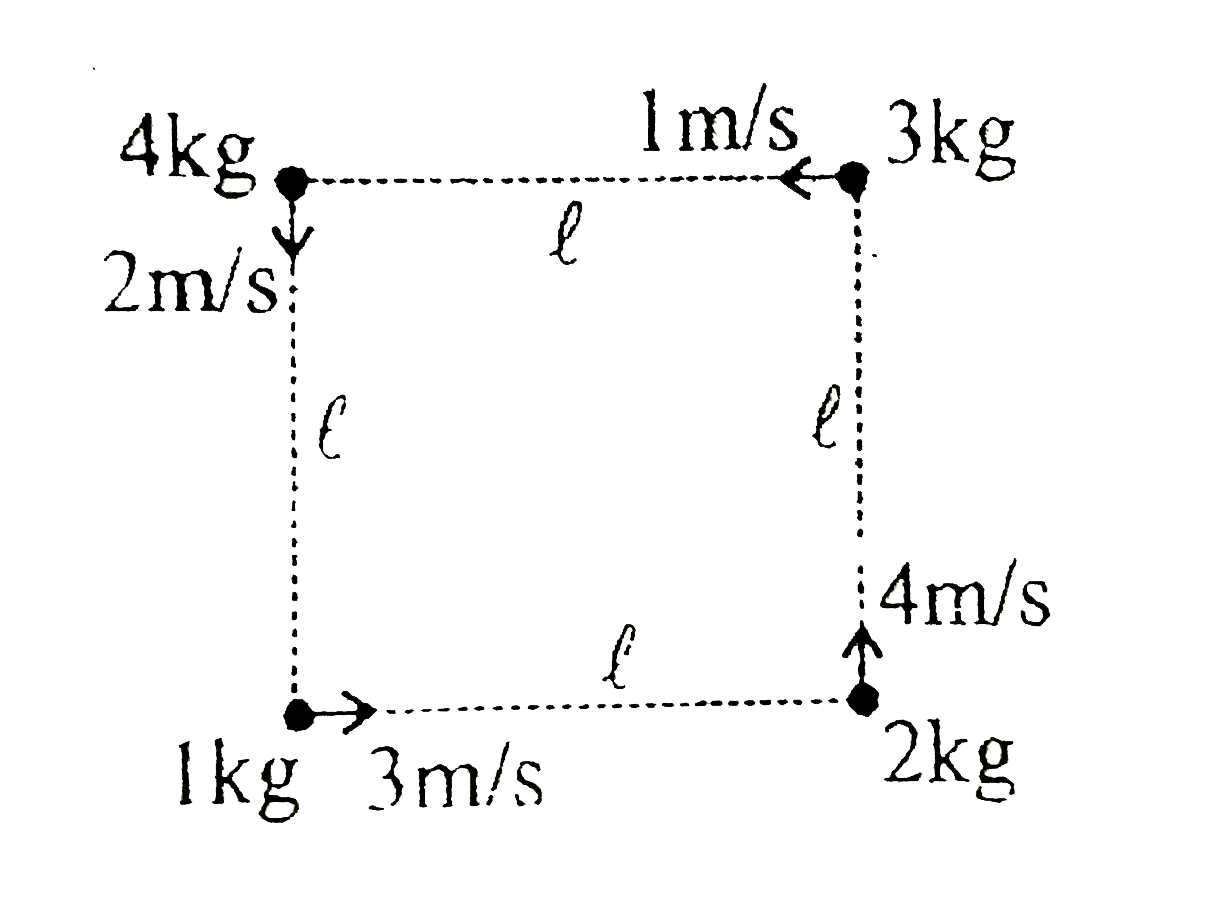A $3 k g m s^{- 1}$
B $5 k g m s^{- 1}$
C $6 k g m s^{- 1}$
DZero
Question 2 - Select One
Three particles of masses $1 k g, 2 k g$ and $3 k g$ are situated at the corners of an equilateral triangle move at speed $6 m s^{- 1}, 3 m s^{- 1}$ and $2 m s^{- 1}$ respectively. Each particle maintains a direction towards the particles at the next corners symmetrically. Find velocity of $C M$ of the system at this instant
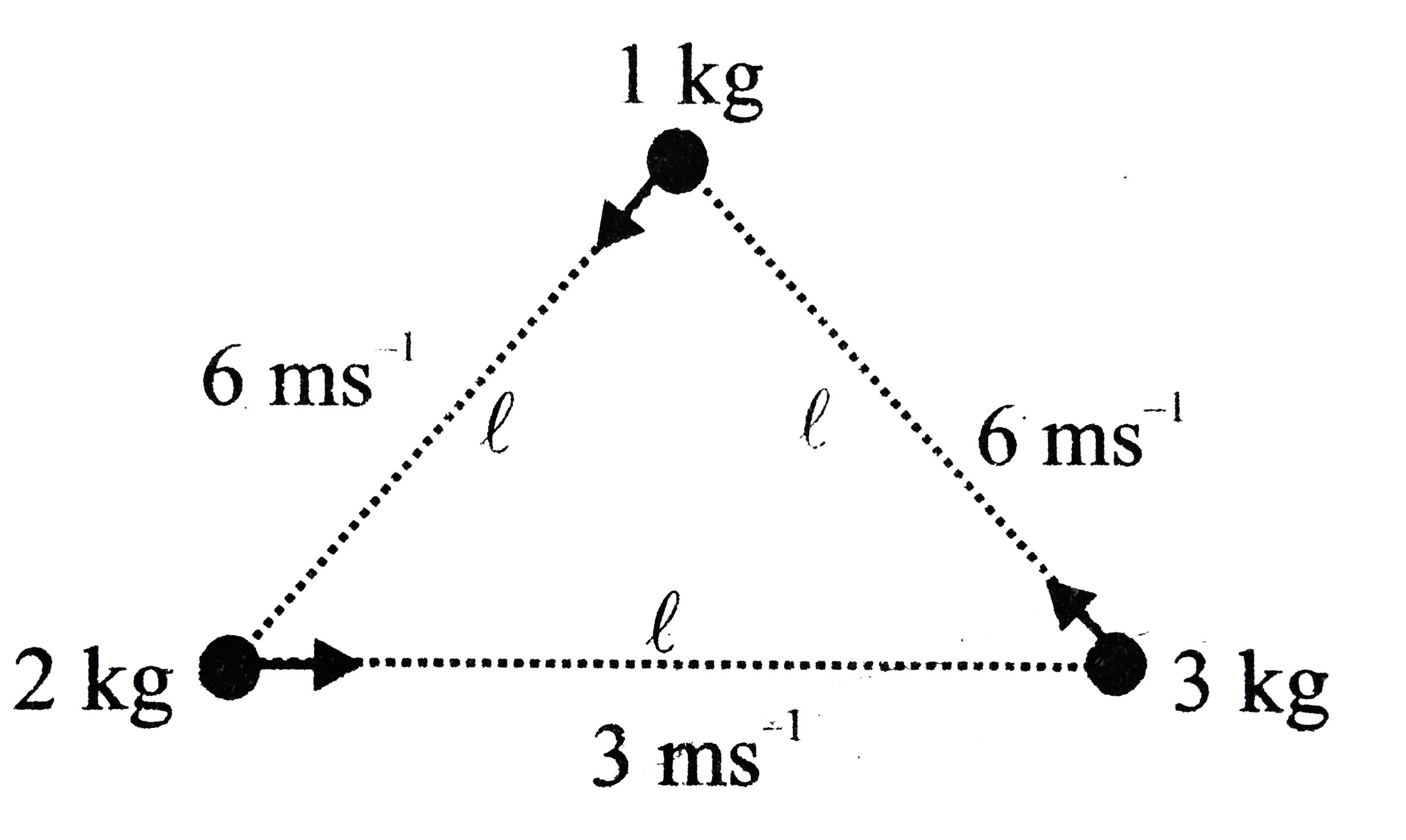A $3 m s^{- 1}$
B $5 m s^{- 1}$
C $6 m s^{- 1}$
Dzero
Question 3 - Select One
Four particles each of mass m are placed at the vertices of a square of side $l$ . the potential at the centre of square is
A $- 2 \sqrt{2} \frac{G m}{l}$
B $- 3 \sqrt{2} \frac{G m}{l}$
C $- 2 \frac{G m}{l}$
D $- 4 \sqrt{2} \frac{G m}{l}$

MOTION-KINEMATICS-EXERCISE 2 OBJECTIVE PROBLEMS

Home
Ask Doubt
Profile