Jack waters his lawn with a sprinkler that sprays water in a circular pattern. The maximum reach of the sprinkler is 15 feet , and the sprinkler head rotates through an angle of 300∘ , as shown in the diagram below . The sprinkler head is represented at point O.

To the nearest square foot , what is the area of the lawn (the shaded area ) that receives water from the sprinkler ?
79
589
94
707
The correct Answer is:B
Step by step video, text & image solution for Jack waters his lawn with a sprinkler that sprays water in a circular pattern. The maximum reach of the sprinkler is 15 feet , and the sprinkler head rotates through an angle of 300^@ , as shown in the diagram below . The sprinkler head is represented at point O. To the nearest square foot , what is the area of the lawn (the shaded area ) that receives water from the sprinkler ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATH Book:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATH Exercise:PRACTICE TEST
Explore 24 Videos
- 1600 CLUB BACKGROUND TOPICSBook:ENGLISH SATChapter:1600 CLUB BACKGROUND TOPICSExercise:PRACTICE TEST
Explore 11 Videos
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:EXERCISE
Explore 45 Videos
Similar Questions

A lawn sprinkler sprays water in a circular pattern at a distance of 15 feet from the sprinkler head which rotates through the angle of 5π3 radians, as shown by the shaded area in the diagram above. What is the area of the lawn, to the nearest square foot, that recieves water from this sprinkler?
View SolutionIn the diagram give n below shaded part represents :-
View Solution
Knowledge Check

In the diagram above, the circle has center O and diameter ¯¯¯¯¯¯AC. The measure of arc AB is 120∘ , and AO=4. What is the area of the shaded region ?A16π3−8√3B8π3−2√3C8π3−4√3D8π3−8√3What is the area, in square feet, of the figure below?
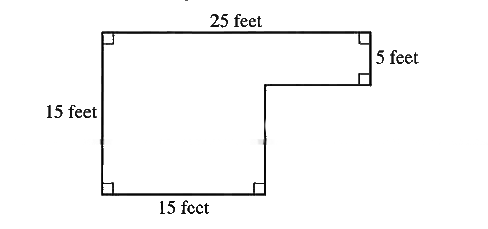 A60B80C275D375
A60B80C275D375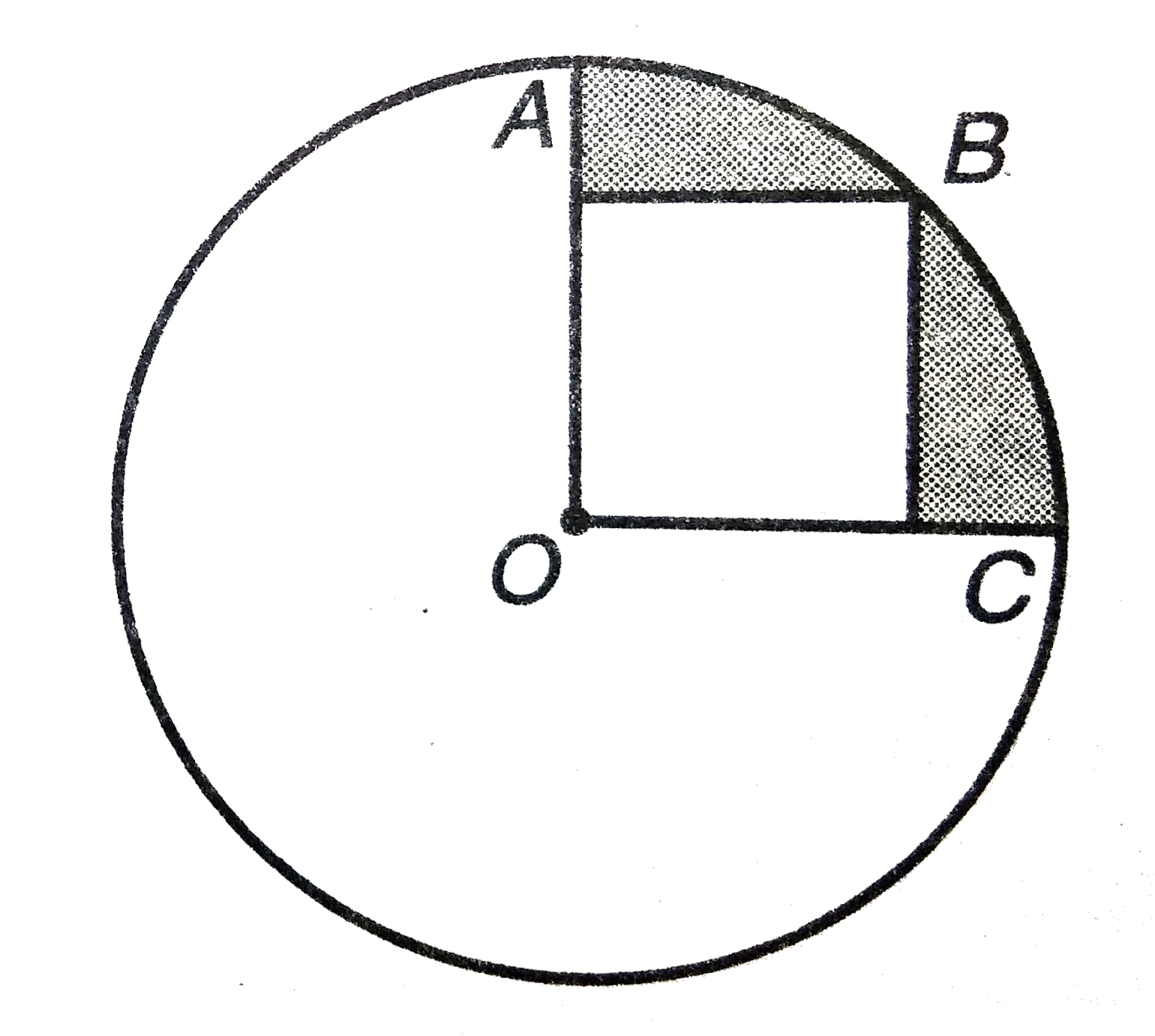
In the figure above, OABC is a square and B is a points on the circle with center O. If AB=6, what is the area of the shaded region?A9(π−2)B9(π−1)C12(π−2)D18(π−2)
A square lawn is surrounded by a path 2.5 m wide. If the area of the path is 165 m2 , find the area of the lawn.
View Solution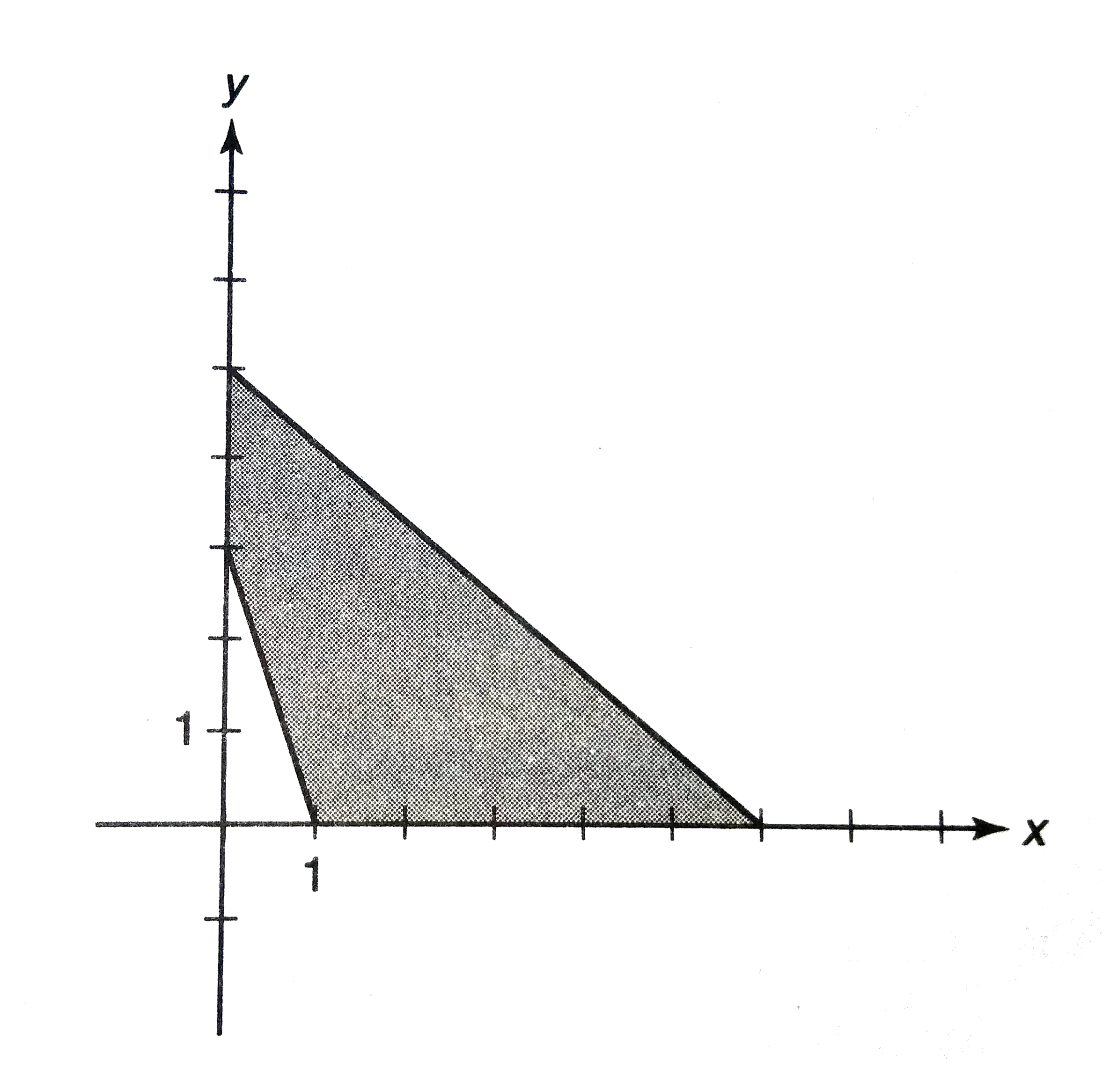
In the figure above, what is the number of square units in the area of the shaded region?
View Solution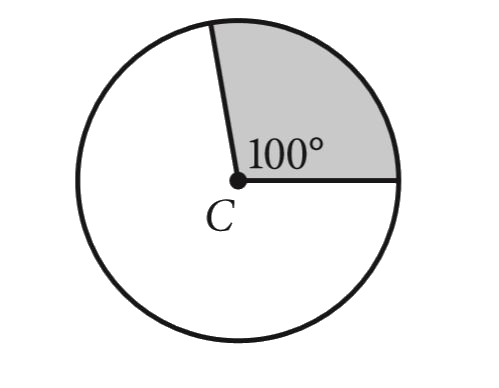
Point C is the center of the circle above. What fraction of the area of the circle is the area of the shaded region?
View Solution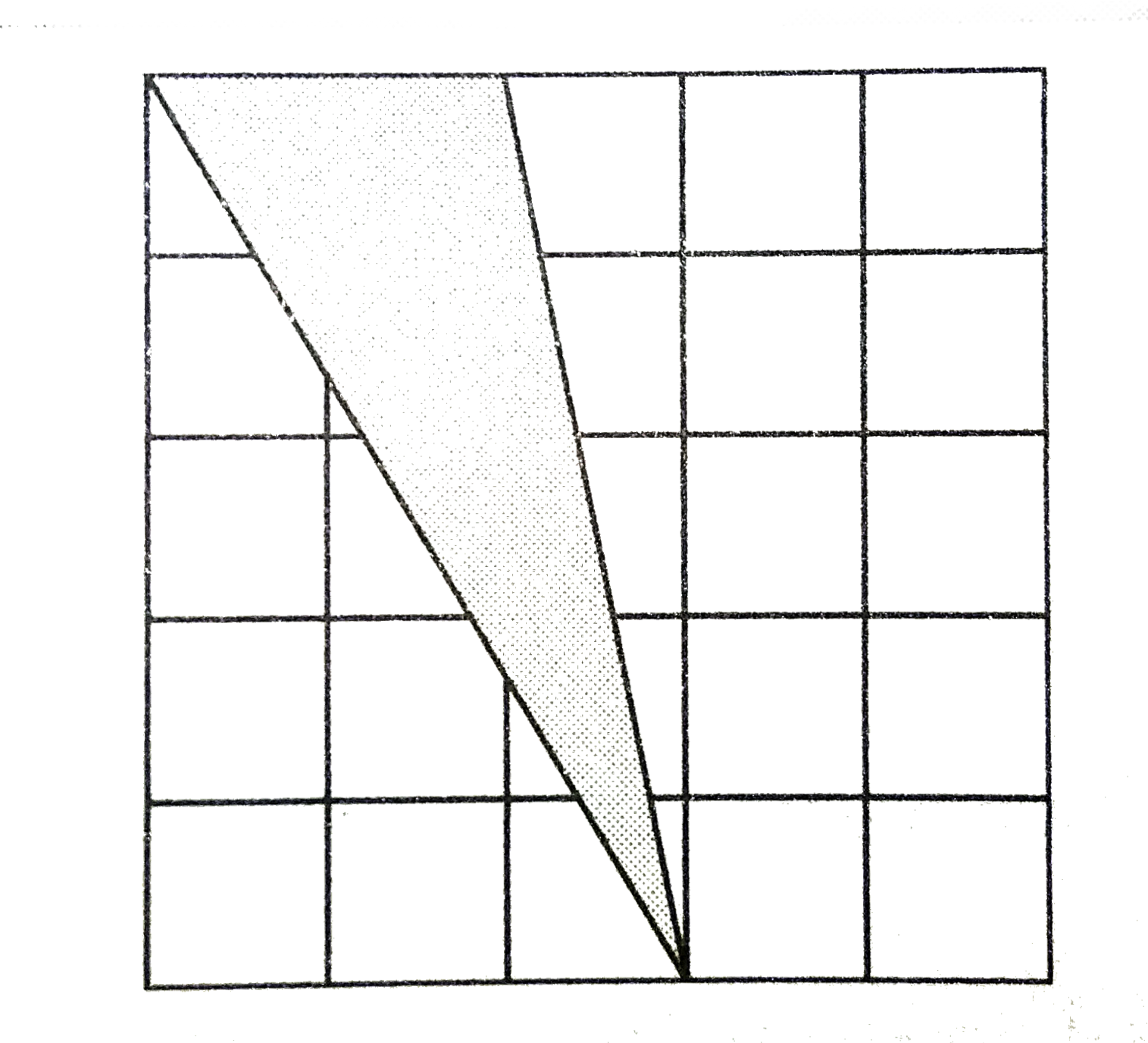
Each of the small squares in the figure above has an area of 4. If the shortest , what is the area of the shaded triangle?
View SolutionThe rectangle shown in the figure below is partitioned into 3 triangles, 2 of which are shaded. What is the total area, in square inches, of the 2 shaded regions?

View Solution

