
A lawn sprinkler sprays water in a circular pattern at a distance of 15 feet from the sprinkler head which rotates through the angle of 5π3 radians, as shown by the shaded area in the diagram above. What is the area of the lawn, to the nearest square foot, that recieves water from this sprinkler?
The correct Answer is:589
Step by step video, text & image solution for A lawn sprinkler sprays water in a circular pattern at a distance of 15 feet from the sprinkler head which rotates through the angle of (5pi)/(3) radians, as shown by the shaded area in the diagram above. What is the area of the lawn, to the nearest square foot, that recieves water from this sprinkler? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:EXERCISE
Explore 45 Videos
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:Multiple Choice
Explore 99 Videos
- ADDITIONAL TOPICS IN MATH Book:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATH Exercise:PRACTICE TEST
Explore 24 Videos
- COMPLEX NUMBERSBook:ENGLISH SATChapter:COMPLEX NUMBERSExercise:EXERCISE
Explore 6 Videos
Similar Questions
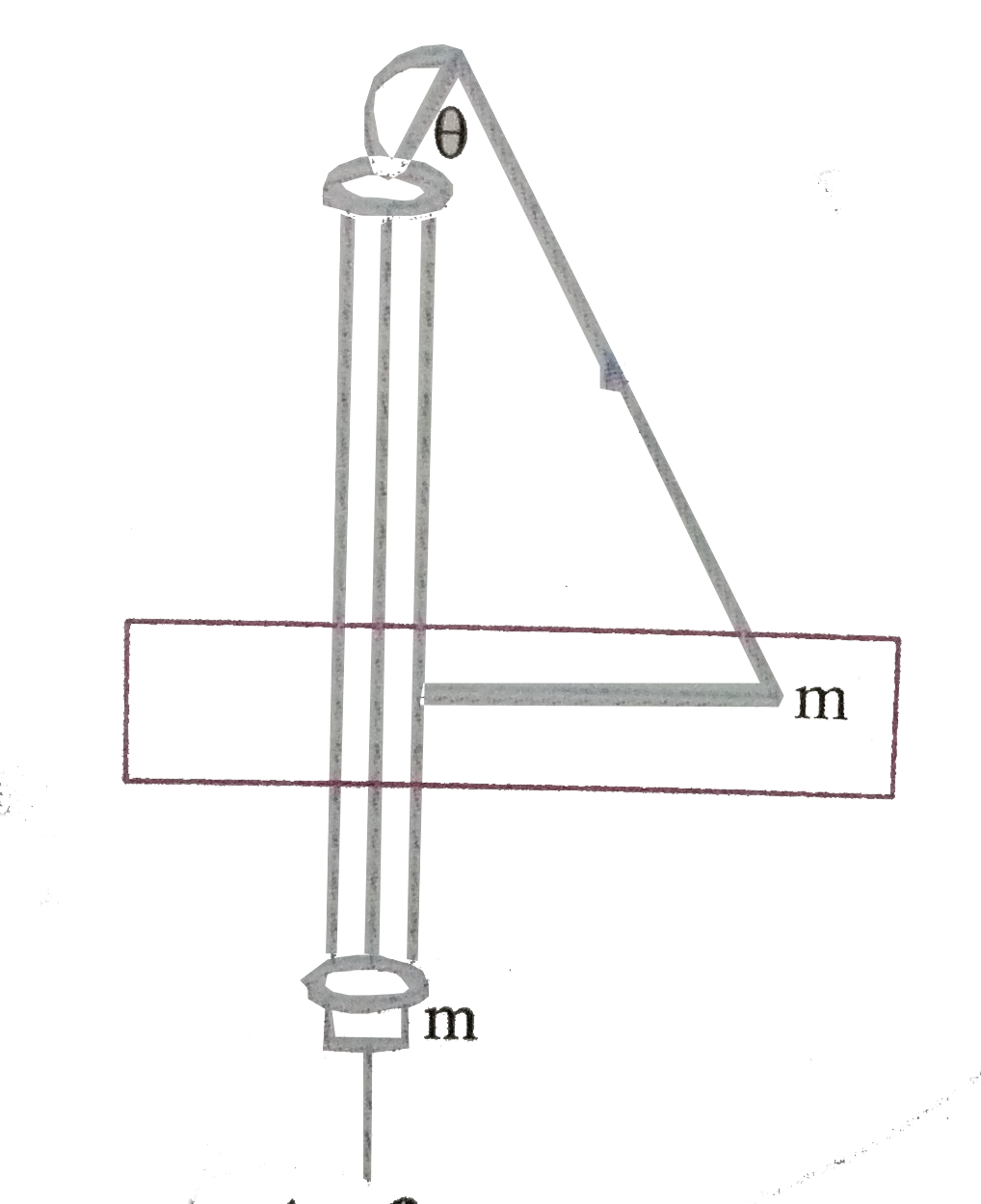
A large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular path which lies in a horizantal plane. The length of the string from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
View SolutionA circular flower garden has an area of 314m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12m. Will the sprinkler water th entire garden ? (Take pπ=3.14)
View Solution
Knowledge Check
Jack waters his lawn with a sprinkler that sprays water in a circular pattern. The maximum reach of the sprinkler is 15 feet , and the sprinkler head rotates through an angle of 300∘ , as shown in the diagram below . The sprinkler head is represented at point O.

To the nearest square foot , what is the area of the lawn (the shaded area ) that receives water from the sprinkler ?A79B589C94D707In the figure below, a highway rest area (at D) and radar stations (at A and B) lie on a level east-west line, A is 9,000 feet due west of D. An airplane (at C) is shown directly above the rest area, flying due west at a constant speed of 300 feet per secod and at a constant altitude of 12,000 feet. The airplane is located at a straight-line distance of 15,000 feet from the radar station at A and 13,000 feet from the radar station at B.
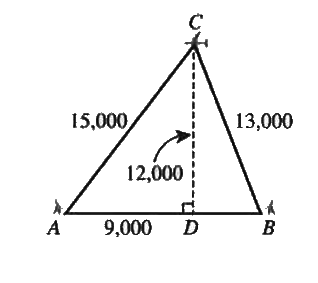
When considering the changing triangle formed by A, B and the moving airplane (C), which of the angles below increases in measure as the airplane flies due west beyond the point directly above A?
I. ∠A
II. ∠B
III. ∠C.AI onlyBII onlyCI and II onlyDI and III onlyIn the figure below, a highway rest area (at D) and radar stations (at A and B) lie on a level east-west line, A is 9,000 feet due west of D. An airplane (at C) is shown directly above the rest area, flying due west at a constant speed of 300 feet per secod and at a constant altitude of 12,000 feet. The airplane is located at a straight-line distance of 15,000 feet from the radar station at A and 13,000 feet from the radar station at B.
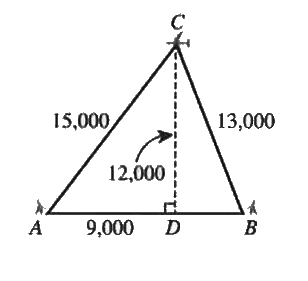
Which of the following values is closest to the number of seconds it will take for the airplane to fly from C to the point directly above the radar station at A?A17B30C40D43
In a garden a spherical sprinkler is used at the end of the lose from which the speed of the flowing water is the same to every direction. The water beam which is directed vertically upward reaches a height of h. Once the sprinkler is placed to the ground and at another time ti a height of h. By what factor will the watered area of greater in the second case ? (Neglect air resistance and consider the pressure in the sprinkler constant.)
View SolutionCurved surface of a vessel has shape of truncated cone having semi-vertex angle 37∘. Vessel is full of water (density ρ=1000kg/m3) upto a height of 13cm and is placed on a smooth horizontal plane. Upper surface is opened to atmosphere. A hole of 1.5cm is made on curved wall of a height of 8cm from bottom as shown in figure. Area of water surface in the vessel is large as compared to the area of the hole.

The initial horizontal range of water from point B is
View SolutionWater is dripping out from a conical funnel of semi-vertical angle π4 at the uniform rate of 2cm3/sec in its surface area through a tiny hole at the vertex in the bottom. When the slant height of the water is 4cm, find the rate of decrease of the slant height of the water.
View SolutionWater is dripping out from a conical funnel of semi-vertical angle π4 at the uniform rate of 2cm3/sec in its surface area through a tiny hole at the vertex in the bottom. When the slant height of the water is 4cm, find the rate of decrease of the slant height of the water.
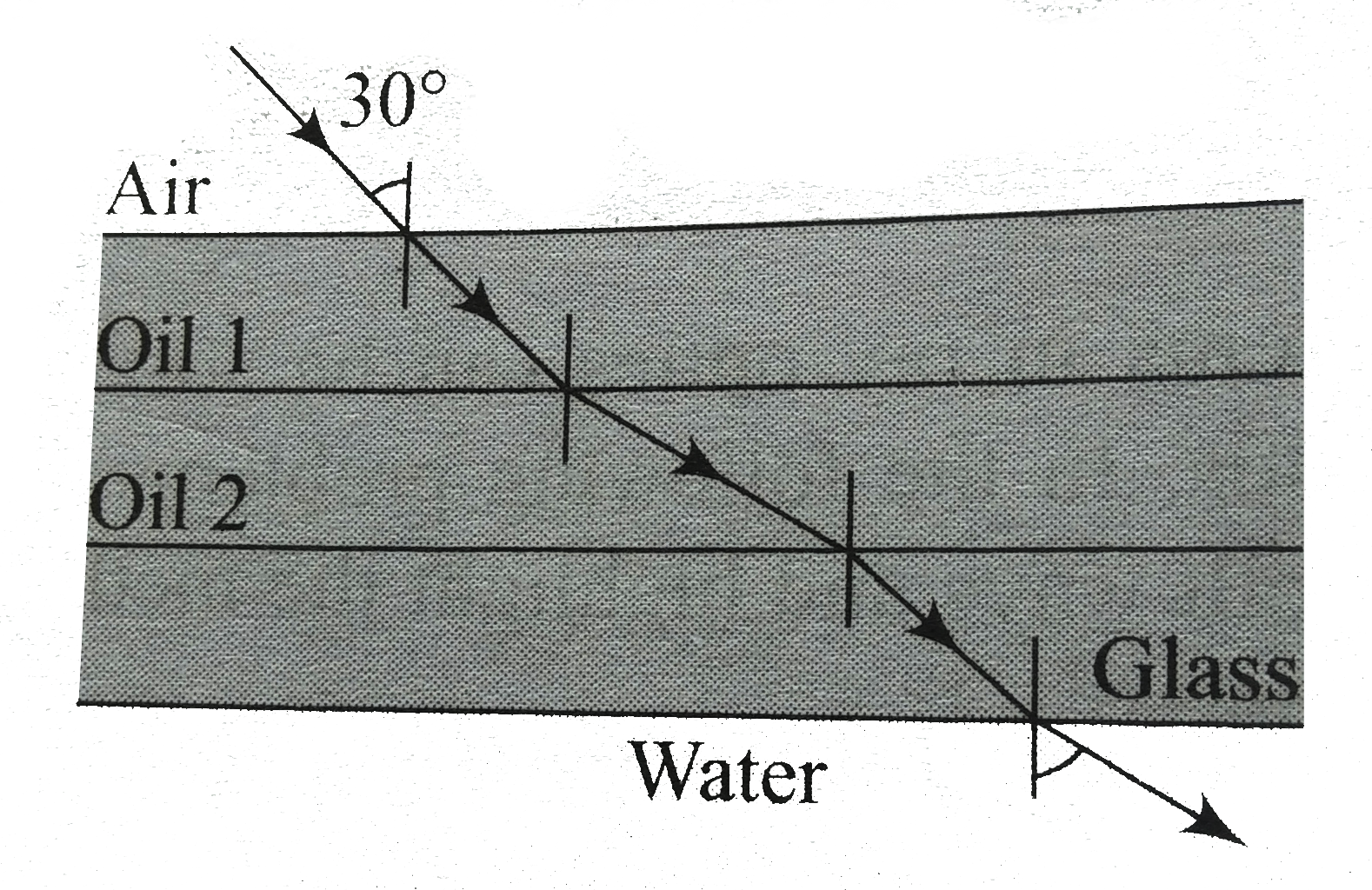
View SolutionLight is incident from air on an oil layer at an incident angle of 30∘. After moving through the oil 1, oil 2, and glass it enters water. If the refraction index of glass and water are 1.5 and 1.3, respectively. Find the angle which the ray makes with the normal in water.
View Solution

