The height reached in time t by a particle thrown upward with a speed u is given by
h=ut−12gt2
where g is acceleration due to gravity. Find the time taken in reaching the maximum height.
Here h=f(t).
Thus h will be maximum when dhdt=0
We have h=ut−12gt2
or dhdt=u−12g(2t)=u−gt
for maximum h, dhdt=0
⇒ u−gt=0
t=ug
Topper's Solved these Questions
Similar Questions
The height reached in time t by a particle thrown upwared with a speed u is given by
h=ut−12>2
where g=9.8 m/s^2 is a constant.Find the timetakenin raching the maximum height.
View SolutionWhat will be the instaneous acceleration of an object thrown upward, when it reaches maximum height?
View Solution
Knowledge Check
Find ratio of acceleration due to gravity g at depth d and at height h where d=2h
A1:1B1:2C2:1D1:4A stone thrown vertically upward satisfies the equation s=64t−16t2 where is in meter and t is second .What is the time required to reach the maximum height ?
A1sB2sC3sD4sIf retardation produced by air resistances to projectile is one-tenth of acceleration due to gravity, the time to reach maximum height approximately-
Aincrease by 9%Bdecrease by 9%Cincrease by 11%Ddecrease by 11%
In the previous problem, the time taken to reach the maximum height will be decreased by:
View SolutionFrom a tower of height H, a particle is thrown vertically upwards with a speed u . The time taken by the particle , to hit the ground , is n times that taken by it to reach the highest point of its path. The relative between H,uandn is :
View SolutionAssertion : A body is dropped from height h and another body is thrown vertically upwards with a speed √gh. They meet at height h2.
Reason : The time taken by both the blocks in reaching the height h2 is same.
View SolutionThe maximum height is reached is 5s by a stone thrown vertically upwards and moving under the equation 10s=10ut−49t2, where s is in metre and t is in second. The value of u is
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
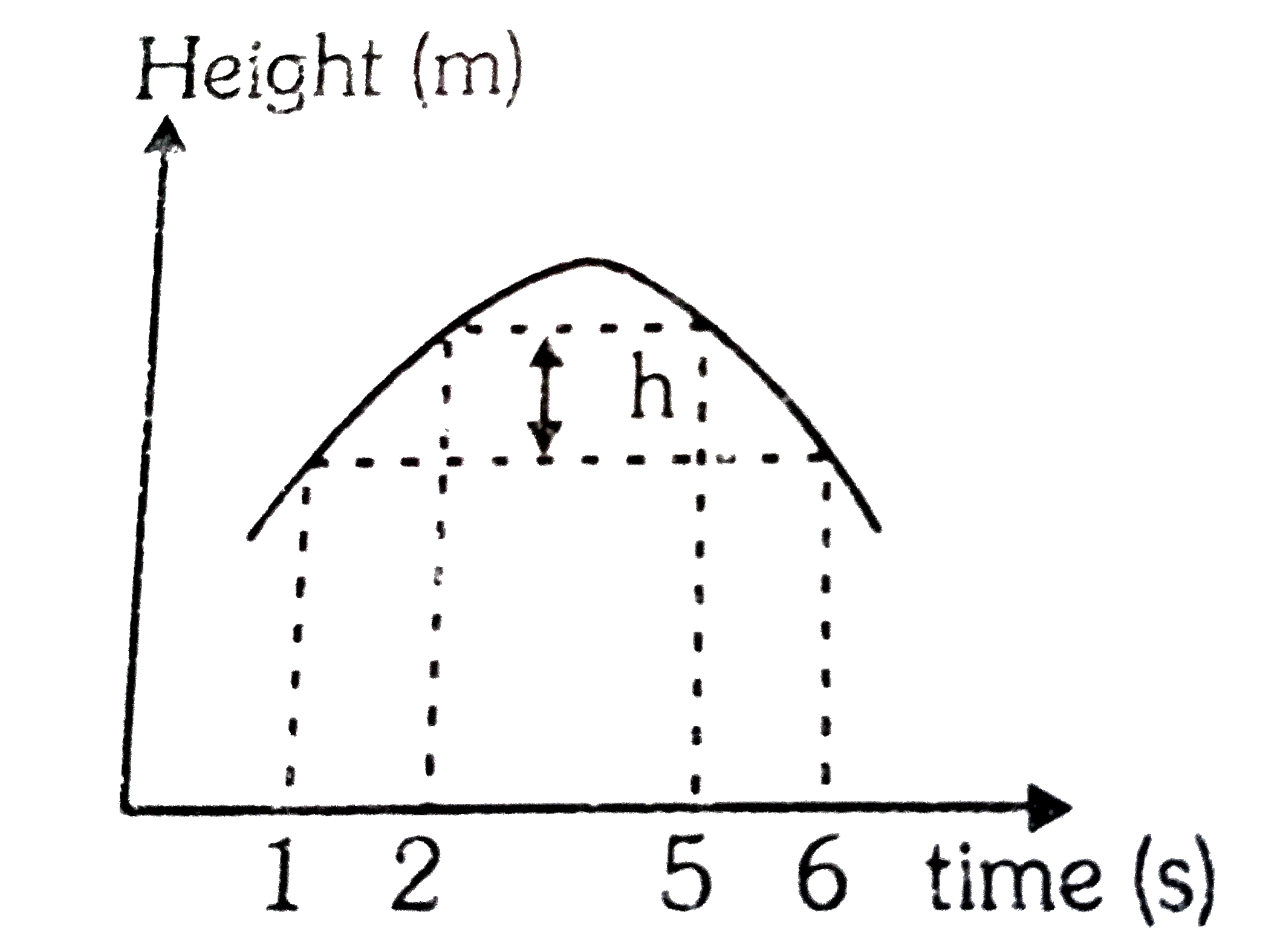
View Solution

