A Merry -go-round, made of a ring-like platform of radius RandmassM, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as see from the round). The speed of the round after wards is
2ω
ω
ω2
0
The correct Answer is:A
As no external torque acts on the system angular momentum should be conserved
Hence, Iω= constant
where, I is moment of inertia of the system and ω is angular velocity of the system
From Eq. (i) I1ω1=I2ω2
(where ω1andω2 are angular velocities before and after jumping)
⇒Iω=I2×ω2
(as mass reduced to half, hence, moment of inertia also reduced to half)
⇒ω2=2ω.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(B) Chapter Exercises
Explore 25 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:Check point 9.3
Explore 15 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Integer type q.
Explore 15 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
A person of mass m stands at the edge of a circular platform of radius R and moment of inertia. A platform is at rest initially. But the platform rotate when the person jumps off from the platform tangentially with velocity u with respect to platfrom. Determine the angular velocity of the platform.
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
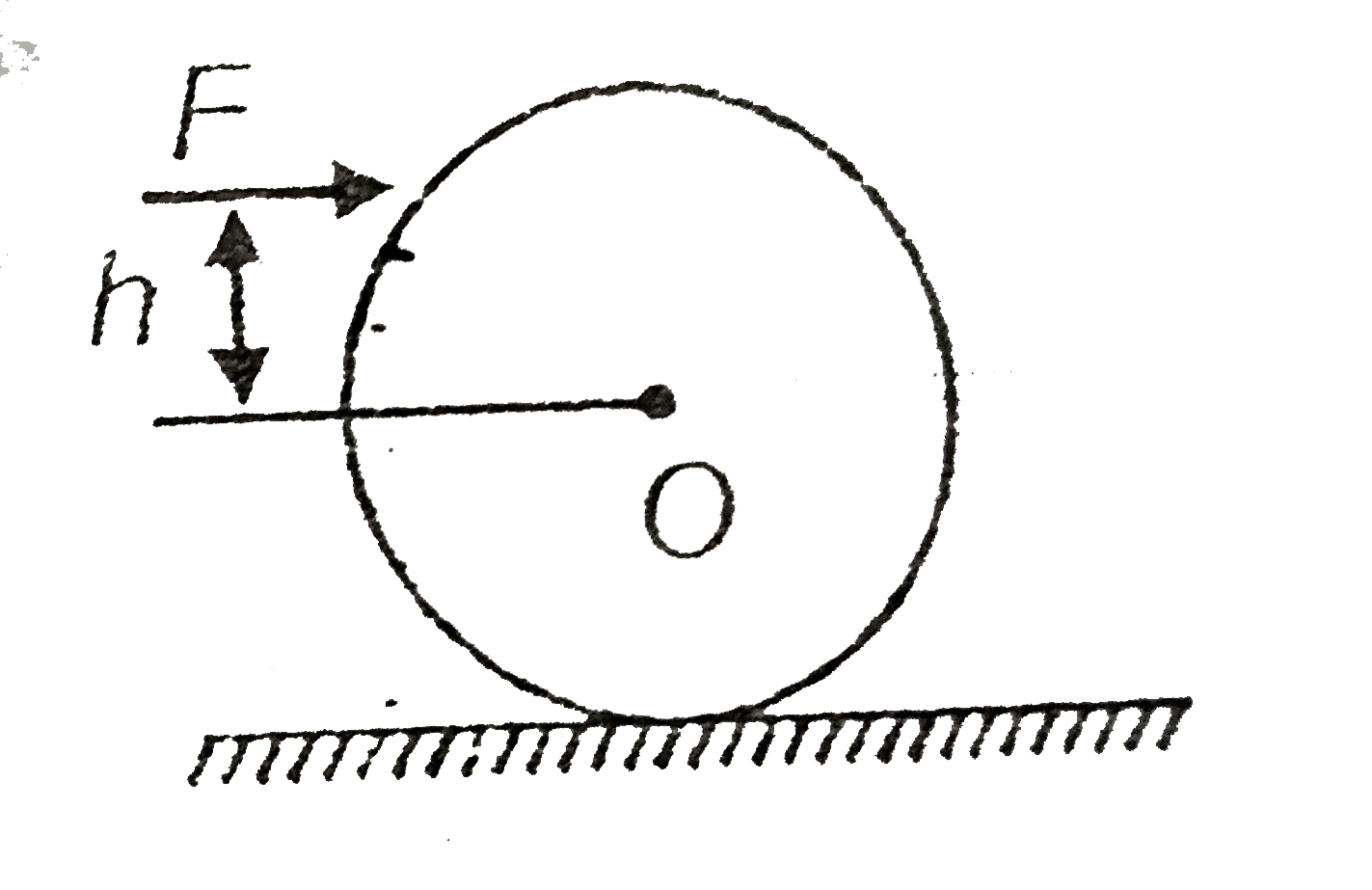
View Solution
Knowledge Check
A Meery -go-round, made of a ring-like plarfrom of radius RandmassM, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially awaay from the centre of the round (as see from the round). The speed of the round after wards is
A2ωBωCω/2D0A merry-go-round, made of ring-like platform of radius R and mass M is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round of afterward is ............
A2ωBωCω2D0A merry -go-round , made of a ring-like platform of radius R and mass M, is revolving with angular speed ω . A person of mass M is standing on it . At one instant , the person jumps off the round , radially away from the centre of the round . The speed of the round afterwards is
A2ωBωCω2D0
A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionA girl of mass M stands on the rim of a frictionless merry-go-round of radius R and rotational inertia I that is not moving. She throws a rock of mass m horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the rock. relative to the ground, is v. After, the linear speed of the girl is.
 .
.
View SolutionA child is standing on the edge of a merry-go-round that has the shape of a disk, as shown in the figure. The mass of the child is 40 kg. The merry-go-round has a mass of 200kg and a radius of 2.5 m, and it is rotating with an angular velocity of ω=2.0 radians per second. The child then walks slowly towards the centre of the merry-go-round. What will be the final angular velocity of the merry-go-round when the child reaches the centre? (The size of the child can be neglected)

View SolutionA planet of mass m is revolving round the sun (of mass Ms) in an elliptical orbit. If →v is the velocity of the planet when its position vector from the sun is →r, then areal velocity of the positon vector of the planet is :
View SolutionTwo satellites of same mass are orbiting round the earth at heights of r1 and r2 from the centre of earth. Their kinetic energies are in the ratio of :
View Solution

