Point X and Y lie on a circle with center C such that the measure of the minor are formed by central angle XCY is 310 of the circumference of the circle. What is the measure of angle XYC, in radians?
310π
35π
65π
53π
The correct Answer is:B
To find the measure of angle XYC in radians, we can follow these steps:
Step 1: Understand the relationship between the arc length and the central angle
The arc length (s) of a circle is related to the radius (r) and the central angle (θ in radians) by the formula:
s=r⋅θ
Step 2: Determine the arc length based on the given information
We know that the measure of the minor arc XY is 310 of the circumference of the circle. The circumference (C) of a circle is given by:
C=2πr
Thus, the arc length (s) can be expressed as:
s=310⋅C=310⋅2πr
Step 3: Substitute the arc length into the formula for arc length
Now, substituting the expression for arc length into the formula s=r⋅θ:
310⋅2πr=r⋅θ
Step 4: Simplify the equation
We can simplify this equation by dividing both sides by r (assuming r≠0):
310⋅2π=θ
Step 5: Calculate the value of θ
Now, we can calculate θ:
θ=310⋅2π=6π10=3π5
Conclusion
Thus, the measure of angle XYC in radians is:
θ=3π5
The arc length (s) of a circle is related to the radius (r) and the central angle (θ in radians) by the formula:
s=r⋅θ
We know that the measure of the minor arc XY is 310 of the circumference of the circle. The circumference (C) of a circle is given by:
C=2πr
Thus, the arc length (s) can be expressed as:
s=310⋅C=310⋅2πr
Now, substituting the expression for arc length into the formula s=r⋅θ:
310⋅2πr=r⋅θ
We can simplify this equation by dividing both sides by r (assuming r≠0):
310⋅2π=θ
Now, we can calculate θ:
θ=310⋅2π=6π10=3π5
Thus, the measure of angle XYC in radians is:
θ=3π5
Topper's Solved these Questions
- ADDITIONAL TOPICSBOOK - PRINCETONCHAPTER - ADDITIONAL TOPICSEXERCISE - QUICK QUIZ #7
3 Videos
- ADDITIONAL TOPICSBOOK - PRINCETONCHAPTER - ADDITIONAL TOPICSEXERCISE - QUICK QUIZ #8
3 Videos
- ADDITIONAL TOPICSBOOK - PRINCETONCHAPTER - ADDITIONAL TOPICSEXERCISE - QUICK QUIZ #5
3 Videos
- ADVANCED ARITHMETICBOOK - PRINCETONCHAPTER - ADVANCED ARITHMETICEXERCISE - Examples
25 Videos
Similar Questions

In the circle above, point A is the center and the length of arc ⌢BC is 25 of the circumference of the circle. What is the value of x ?
View SolutionIn a circle with center O, central angle AOB has a measure of 5π4 radians. The area of the sector formed by central angle AOB is what fraction of the area of the circle?
View Solution
Knowledge Check
What is the angle measure of 4 radians ?
A114.591∘B141.372∘C229.183∘D282.743∘In this triangle, what is the degree measure of angle c ?
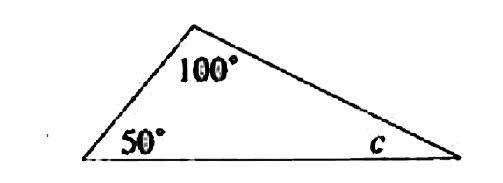 A17B20C30D40
A17B20C30D40In a circle with center O, the measure of central angle POQ is 3π2 radians. The length of the arc formed by central angle POQ is that fraction of the circumference of the circle?
A316B38C34D32
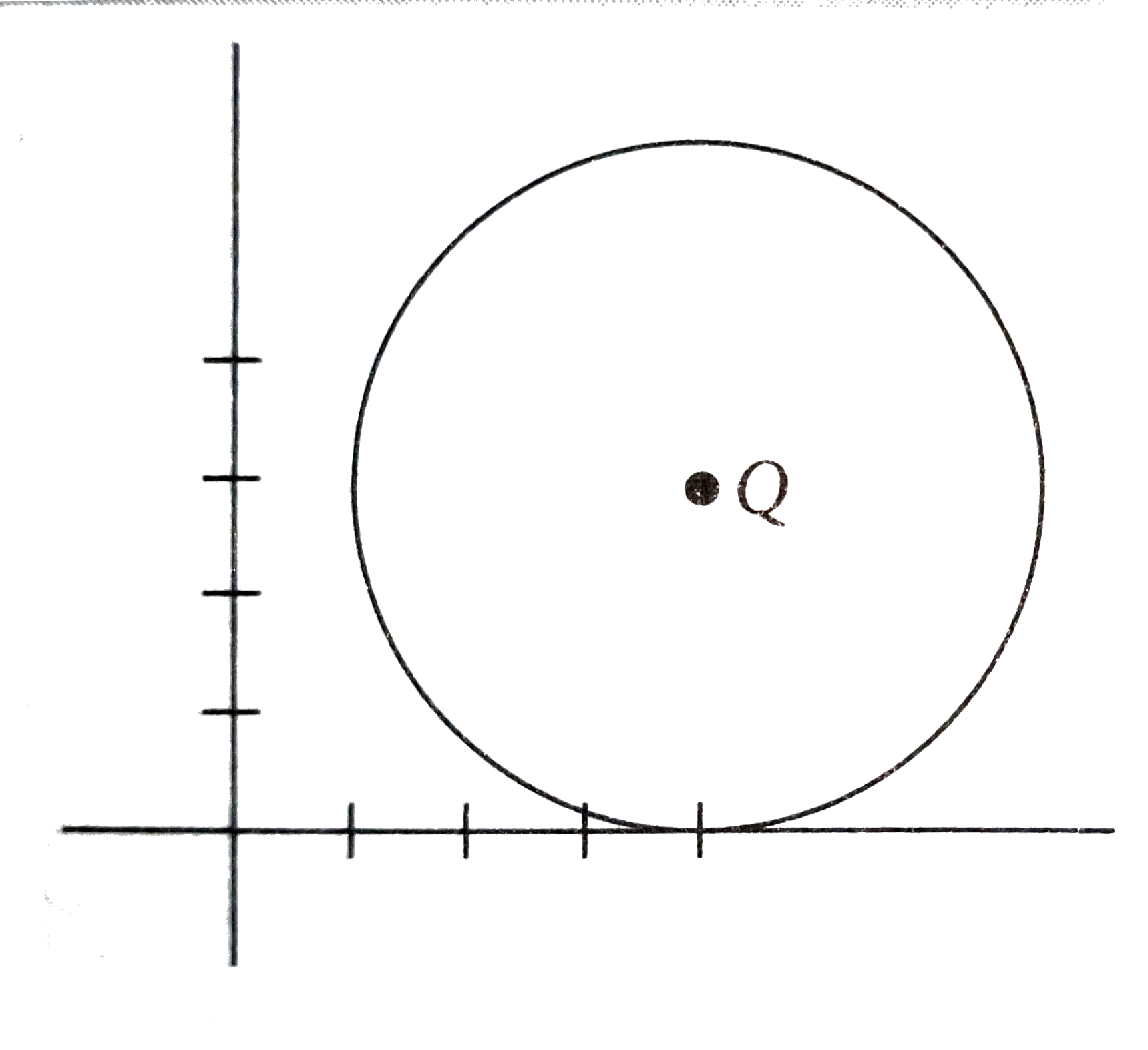
Center Q of the circle above has coordinate of (4,3). What is the circumference of the circle?
View Solution
In the figure above, the circle has center A, and BC=AB. What is the degree measure of the marked angle?
View SolutionWhat is the measure in degrees of an angle that is π4 radians?
View SolutionThe circumference of circle x2+y2−10y−36=0 is
View SolutionWhat is the radian measure of the smaller angle formed by the hands of a clock at 7 o'clock?
View Solution
