There is some change in length when a 33000N tensile force is applied on a steel rod of area of cross-section 10−3m2. The change in temperature of the steel rod when heated is
(Y=3×1011N/m2,α=1.1×10−5/∘C)
20∘C
15∘C
10∘C
0∘C
c) Modulus of elasticity = (Force/Area) ×lΔl
3×1011=3300010−3×lΔl
Δll=3300010−3×13×1011=11×10−5
Charge in length, Δll=αΔT
11×10−5=1.1×10−5×ΔT⇒ΔT=10K or 10∘C
Topper's Solved these Questions
- HEAT, TEMPERATURE AND CALORIMETRYBook:BITSAT GUIDEChapter:HEAT, TEMPERATURE AND CALORIMETRYExercise:Bitsat archives
Explore 9 Videos
- GRAVITATIONBook:BITSAT GUIDEChapter:GRAVITATIONExercise:BITSAT Archives
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:BITSAT GUIDEChapter:LAWS OF THERMODYNAMICSExercise:40
Explore 1 Video
Similar Questions
The force in newton required to increase by 1% length of a rod of area of cross section 10−3m squre is …….., Modulus of elaticity of rod is 1.2×1012Nm−2
View SolutionA steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
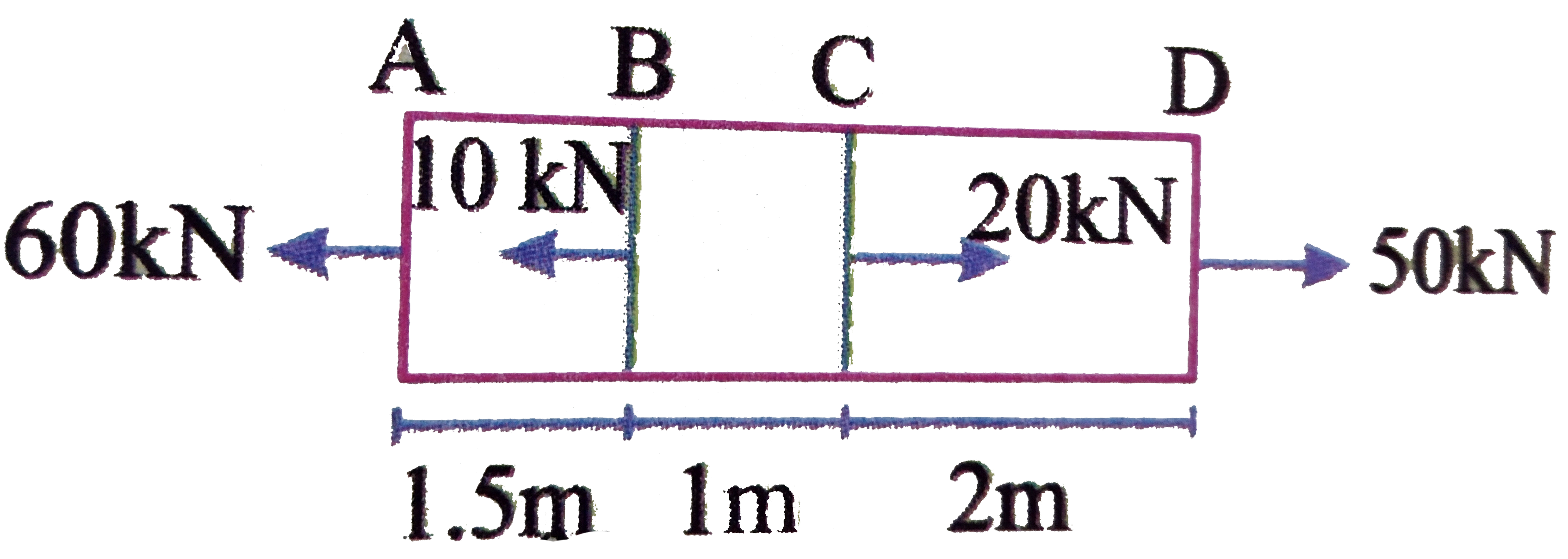
View Solution
Knowledge Check
There is some change in length when a 33000N tensile force is applied on a steel rod of area of cross-section 10−3m2. The change of elongation of the steel rod when heated is
(Y=3×1011N/m2,α=1.1×10−5/∘C)A20∘CB15∘CC10∘CD0∘CThere is same change in length when a 33000 N tensile force is applied on a steel rod of area of cross-section 10−3m2 . The change of temperature required to produce the same elongation, if the steel rod is heated , if (The modulus of elasticity is 3×1011N/m2 and the coefficient of linear expansion of steel is 11×10−5/∘C).
A20∘B15∘C10∘D0∘When a force is applied on a wire of uniform cross-sectional area 3×10−6m2 and length 4 m, the increase in length is 1mm. Energy stored in it will be (Y=2×1011N/m2)
A6270 JB0.177 JC0.075 JD0.150 J
A steel rod of cross-sectional area Im2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2

View SolutionFor increasing the length by 0.5mm in a steel wire of length 4m and area of cross section 5mm2, the force required is (Y=11.90×1012N/m2)
View SolutionA steel wire , of uniform area 2mm2 , is heated up to 50∘C and is stretched by tying its ends rigidly . The change in tension , when the temperature falls from 50∘C to 30∘C is (Take Y=2×1011Nm−2,α=1.1×10−5∘C−1)
View SolutionWhat force should be applied to the ends of steel rod of cross sectional area 10cm2 to prevent it form elongation when heated form 273 K to 303 k ? (α of steel10−5.∘C−1,Y=2×1011NH−2)
View SolutionOn increasing the length by 0.5 mm in a steel wire of length 2 m and area of cross section 2mm2, the force required is [Y for steel =2.2×1011Nm2]
View Solution

