What force should be applied to the ends of steel rod of cross sectional area 10cm2 to prevent it form elongation when heated form 273 K to 303 k ? (α of steel10−5.∘C−1,Y=2×1011NH−2)
2×104N
3×104N
6×104N
12×104N
The correct Answer is:C
To solve the problem of determining the force that should be applied to the ends of a steel rod to prevent elongation when heated from 273 K to 303 K, we can follow these steps:
Step 1: Identify the given values
- Cross-sectional area A=10cm2=10×10−4m2=10−3m2
- Coefficient of linear expansion α=10−5°C−1
- Young's modulus Y=2×1011N/m2
- Initial temperature T1=273K
- Final temperature T2=303K
Step 2: Calculate the change in temperature
ΔT=T2−T1=303K−273K=30K
Step 3: Relate stress, strain, and force
The stress σ in the rod can be expressed as:
σ=Y×strain
where strain can be defined in terms of thermal expansion:
strain=α×ΔT
Step 4: Substitute the expression for strain into the stress formula
Thus, we can write:
σ=Y×(α×ΔT)
Step 5: Relate stress to force
Stress is also defined as force per unit area:
σ=FA
where F is the force and A is the cross-sectional area.
Step 6: Combine the equations to find force
Equating the two expressions for stress:
FA=Y×(α×ΔT)
From this, we can solve for F:
F=A×Y×(α×ΔT)
Step 7: Substitute the known values into the equation
Substituting the values we have:
F=(10×10−4m2)×(2×1011N/m2)×(10−5°C−1)×(30K)
Step 8: Calculate the force
Calculating this step by step:
1. Calculate α×ΔT:
10−5×30=3×10−4
2. Now substitute into the force equation:
F=(10×10−4)×(2×1011)×(3×10−4)
F=10×2×3×10−4×1011×10−4
F=60×103N=6×104N
Final Answer
The force that should be applied to the ends of the steel rod to prevent elongation when heated is:
F=6×104N
- Cross-sectional area A=10cm2=10×10−4m2=10−3m2
- Coefficient of linear expansion α=10−5°C−1
- Young's modulus Y=2×1011N/m2
- Initial temperature T1=273K
- Final temperature T2=303K
ΔT=T2−T1=303K−273K=30K
The stress σ in the rod can be expressed as:
σ=Y×strain
where strain can be defined in terms of thermal expansion:
strain=α×ΔT
Thus, we can write:
σ=Y×(α×ΔT)
Stress is also defined as force per unit area:
σ=FA
where F is the force and A is the cross-sectional area.
Equating the two expressions for stress:
FA=Y×(α×ΔT)
From this, we can solve for F:
F=A×Y×(α×ΔT)
Substituting the values we have:
F=(10×10−4m2)×(2×1011N/m2)×(10−5°C−1)×(30K)
Calculating this step by step:
1. Calculate α×ΔT:
10−5×30=3×10−4
2. Now substitute into the force equation:
F=(10×10−4)×(2×1011)×(3×10−4)
F=10×2×3×10−4×1011×10−4
F=60×103N=6×104N
The force that should be applied to the ends of the steel rod to prevent elongation when heated is:
F=6×104N
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (C.W.)
Explore 20 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - III
Explore 23 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
Similar Questions
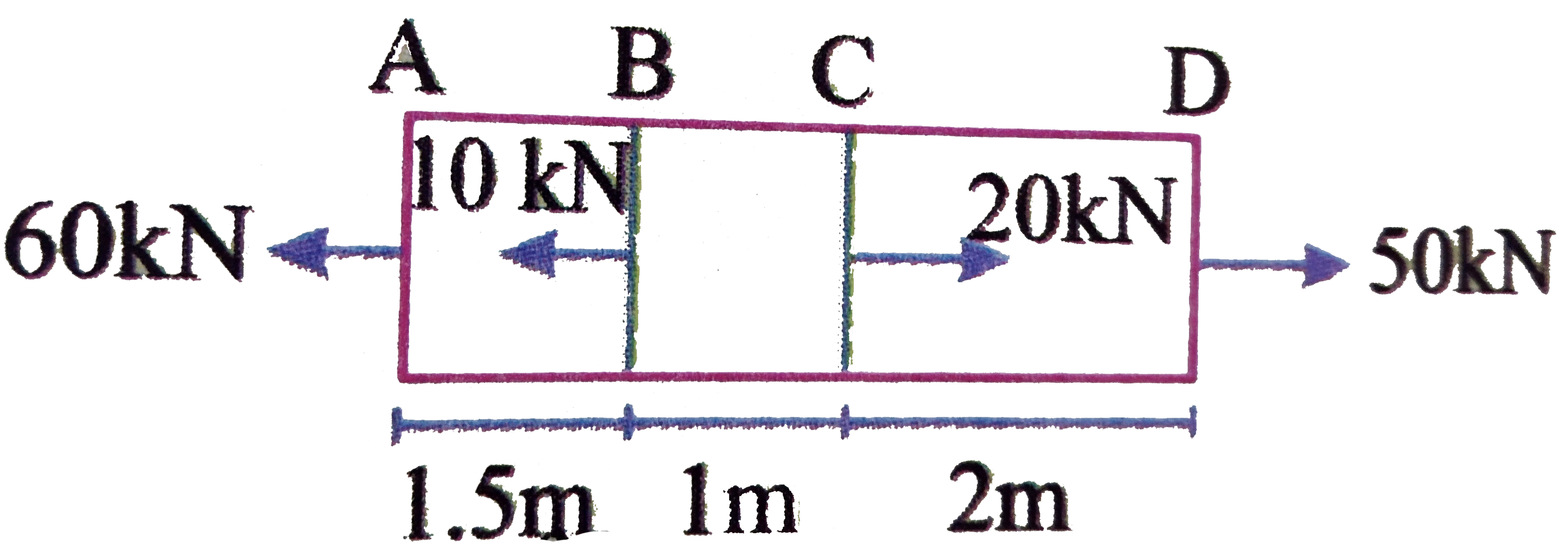
A steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
View SolutionCalculate the force required to increase the length of a steel wire of cross- sectional area 10−6m2 by 0.5% given: Y(for steel)=2×1011N−m2
View Solution
Knowledge Check
There is some change in length when a 33000N tensile force is applied on a steel rod of area of cross-section 10−3m2. The change of elongation of the steel rod when heated is
(Y=3×1011N/m2,α=1.1×10−5/∘C)A20∘CB15∘CC10∘CD0∘CA body of mass 1 kg is fastened to one end of a steel wire of cross- section area 3×10−6m2 and is rotated in horizantal circle of radius 20 cm with a constant speed 2m/s. Find the elongation of the wire (Y=2×1011N/m2)
A0.33×10−5mB0.67×10−5mC2×10−5mD4×10−5A steel rod with a cross-sectional area of 150mm2 is stretched between two fixed points. The tensile load at 20∘C is 5000N.
(a) What will be the stress at −20∘C ?
(b) At what temperature will the stress be zero ?
(Assume α=11.7μm/m∘C and Y=200GN/m2)A12.7×106N/m2B1.27×106N/m2C127×106N/m2D0.127×106N/m2
A steel rod 25 cm long has a cross -sectiional area of 0.8cm2. What force wouyld be required to stretch this rod by the same amount as the expansion produced by heating it by 10∘C? Given that for steel coefficient of linear expansion and Young's modulus are given as α=1.1×10−5.∘C−1 and Y=2×1011Nm−2
View SolutionWhat should be the length of steel and copper rods at 0∘C that the length of steel rod is 5 cm longer than copper at all termperature? Given αCu=1.7×105.∘C−1 and αsteel=1.1×105.∘C−1.
View SolutionWhat will be the stress at −20∘C, if a steel rod with a cross-sectional area of 150 mm2 is stretched between two fixed points. The tensile load at 20∘C is 5000N. (Assume α=11.7×10−6/∘CandY=200×1011N/m2)
View SolutionA 1 m long steel wire of cross-sectional area 1mm2 is extended 1 mm. If Y=2×1011Nm−2, then the work done is
View SolutionThere is same change in length when a 33000 N tensile force is applied on a steel rod of area of cross-section 10−3m2 . The change of temperature required to produce the same elongation, if the steel rod is heated , if (The modulus of elasticity is 3×1011N/m2 and the coefficient of linear expansion of steel is 11×10−5/∘C).
View Solution

