Two balls A and B of angular velocities and collide with each other. Then, after collision
both have same angular velocities
when balls are smooth
when balls are smooth
c) a) This is possible, when balls are is smooth.
b) is not always possible. It depends upon conditions. But no conditions are mentioned .
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:BITSAT GUIDEChapter:ROTATIONAL MOTIONExercise:BITSAT Archives
Explore 9 Videos
- NEWTONS LAWS OF MOTION AND FRICTIONBook:BITSAT GUIDEChapter:NEWTONS LAWS OF MOTION AND FRICTIONExercise:BITSAT Archives
Explore 23 Videos
- SCALARS AND VECTORSBook:BITSAT GUIDEChapter:SCALARS AND VECTORSExercise:All Questions
Explore 34 Videos
Similar Questions
A clutch assembly consists of two discs A and B of moment of inertia 2I and I respectively, one being the engine fly wheel, the other one is the clutch plate. The discs are initially rotaing with angular velocities ωA=ω and ωB=2ω as shown in fig. When the two disc are brought into contact the discs rub against each other and eventually reach a common angualr velocity ω.
(a) Derive an expressio for ω
(b) What is the angular impulse of friction on any one of the discs?

View SolutionTwo discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then

View Solution
Knowledge Check
A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to
 AvBv5C3v5Dv6
AvBv5C3v5Dv6Two particles of mass mA and mB and their velocities are VA and VB respectively collides. After collision they interchanges their velocities, then ratio of mAmB is
AvAvBBvBvACvA+vBvB−vAD1A sphere of radius R and mass M collides elastically with a cubical block of mass M and side 2R. The entire system is on a smooth horizontal ground. Given that the sphere was rolling without slipping with an angular velocity ω at the time of collision. The velocities of the sphere and the block after the collision are
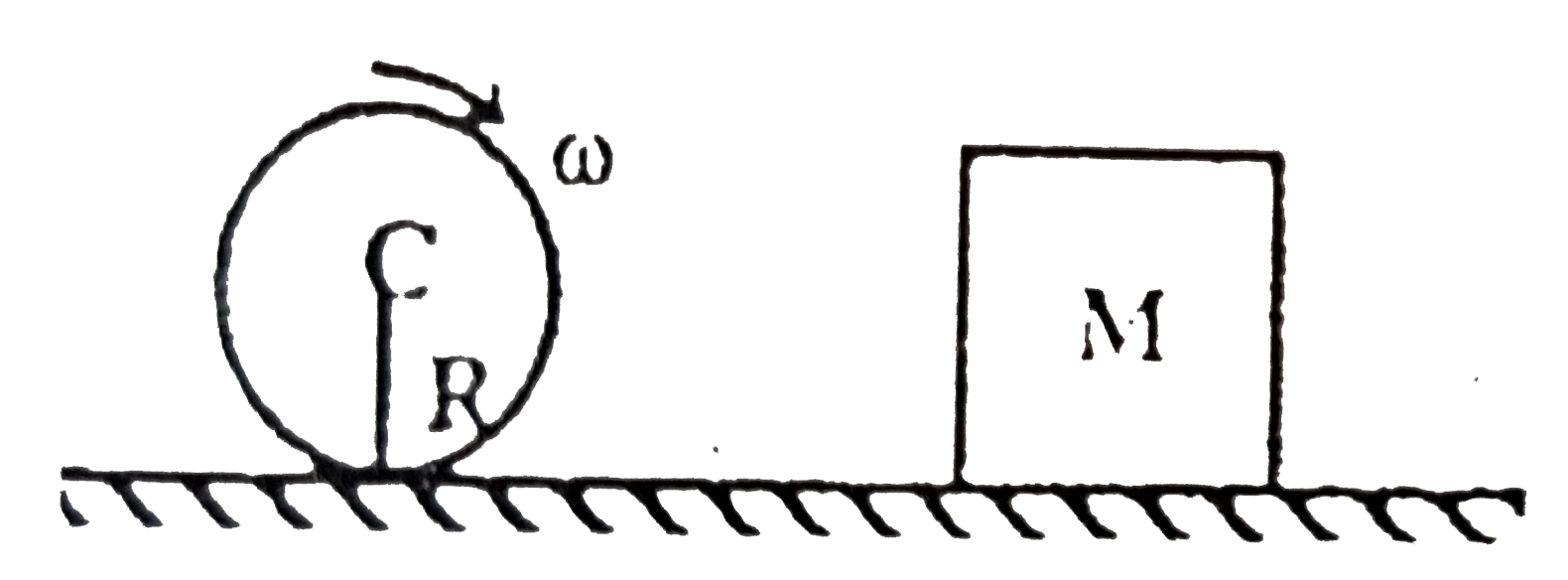 Aωsphere=0, vsphere=0, vblock=vBωsphere=ω, vsphere=0, vblock=vCωsphere=0, vsphere=0, vblock=0Dωsphere=ω2, vsphere=v2, vblock=v2
Aωsphere=0, vsphere=0, vblock=vBωsphere=ω, vsphere=0, vblock=vCωsphere=0, vsphere=0, vblock=0Dωsphere=ω2, vsphere=v2, vblock=v2
Two balls are moving towards each other on a vertical line collides with each other as shown. Find their velocities just after collision.
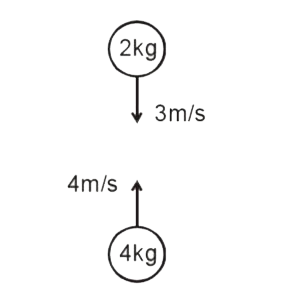
View SolutionTwo indentical balls A and B moving with velocities uA and uB I the same direction collide. Coefficient of restitution is e.
(a) Deduce expression for velocities of the balls after the collision.
(b) If collision is perfectly elastic, what do you observe?
View SolutionA ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionTwo identical balls A and B are released from the position shown in Fig. They collide elastically with each other on the horizontal portion. The ratio of heights attained by A and B after collision is (neglect friction)

View SolutionA sphere is moving on a smooth surface with angular velocity ω and linear velocity v. If collides elastically with another identical sphere B kept at rest. Neglecting friction everywhere, let VA and ωA be linear and angular velocities of sphere A after the impact and let VB and ωB be the corresponding parameters for spehre B. Then
View Solution