A block of mass 0.18 kg is attached to a spring of force constant 2N/m. The coefficient of friction between the block and the floor is 0.1. Initially, the block is at rest and the spring is unstretched. An impulse is given to the block.
The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is v=N/10. Then, N is
2
3
4
6
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the block, the energy transformations involved, and use the given data to find the initial velocity of the block.
Step 1: Identify the given data
- Mass of the block, m=0.18kg
- Spring constant, k=2N/m
- Coefficient of friction, μ=0.1
- Distance slid, x=0.06m
Step 2: Calculate the gravitational force acting on the block
The gravitational force Fg acting on the block can be calculated using:
Fg=m⋅g
where g≈9.81m/s2.
Calculating:
Fg=0.18kg⋅9.81m/s2=1.764N
Step 3: Calculate the frictional force
The frictional force Ff can be calculated using:
Ff=μ⋅Fg=μ⋅m⋅g
Calculating:
Ff=0.1⋅1.764N=0.1764N
Step 4: Calculate the work done against friction
The work done against friction Wf when the block slides a distance x is given by:
Wf=Ff⋅x
Calculating:
Wf=0.1764N⋅0.06m=0.010584J
Step 5: Set up the energy conservation equation
The initial kinetic energy KE of the block when it is given an impulse is equal to the work done against friction plus the potential energy stored in the spring when it is compressed:
12mv2=Wf+12kx2
Step 6: Calculate the potential energy stored in the spring
The potential energy PE stored in the spring when compressed by x is given by:
PE=12kx2
Calculating:
PE=12⋅2N/m⋅(0.06m)2=12⋅2⋅0.0036=0.0036J
Step 7: Substitute values into the energy equation
Substituting the values into the energy equation:
12⋅0.18⋅v2=0.010584+0.0036
Calculating the right side:
12⋅0.18⋅v2=0.014184
Step 8: Solve for v2
Now, solving for v2:
0.09⋅v2=0.014184
v2=0.0141840.09=0.1576
Step 9: Calculate v
Taking the square root to find v:
v=√0.1576≈0.396m/s
Step 10: Relate v to N
Given that v=N10:
0.396=N10
N=0.396×10=3.96
Conclusion
Since N must be an integer, we round N to the nearest integer:
N≈4
Final Answer
Thus, the value of N is 4.
- Mass of the block, m=0.18kg
- Spring constant, k=2N/m
- Coefficient of friction, μ=0.1
- Distance slid, x=0.06m
The gravitational force Fg acting on the block can be calculated using:
Fg=m⋅g
where g≈9.81m/s2.
Fg=0.18kg⋅9.81m/s2=1.764N
The frictional force Ff can be calculated using:
Ff=μ⋅Fg=μ⋅m⋅g
Calculating:
Ff=0.1⋅1.764N=0.1764N
The work done against friction Wf when the block slides a distance x is given by:
Wf=Ff⋅x
Calculating:
Wf=0.1764N⋅0.06m=0.010584J
The initial kinetic energy KE of the block when it is given an impulse is equal to the work done against friction plus the potential energy stored in the spring when it is compressed:
12mv2=Wf+12kx2
The potential energy PE stored in the spring when compressed by x is given by:
PE=12kx2
Calculating:
PE=12⋅2N/m⋅(0.06m)2=12⋅2⋅0.0036=0.0036J
Substituting the values into the energy equation:
12⋅0.18⋅v2=0.010584+0.0036
Calculating the right side:
12⋅0.18⋅v2=0.014184
Now, solving for v2:
0.09⋅v2=0.014184
v2=0.0141840.09=0.1576
Taking the square root to find v:
v=√0.1576≈0.396m/s
Given that v=N10:
0.396=N10
N=0.396×10=3.96
Since N must be an integer, we round N to the nearest integer:
N≈4
Thus, the value of N is 4.
Topper's Solved these Questions
Similar Questions
A block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
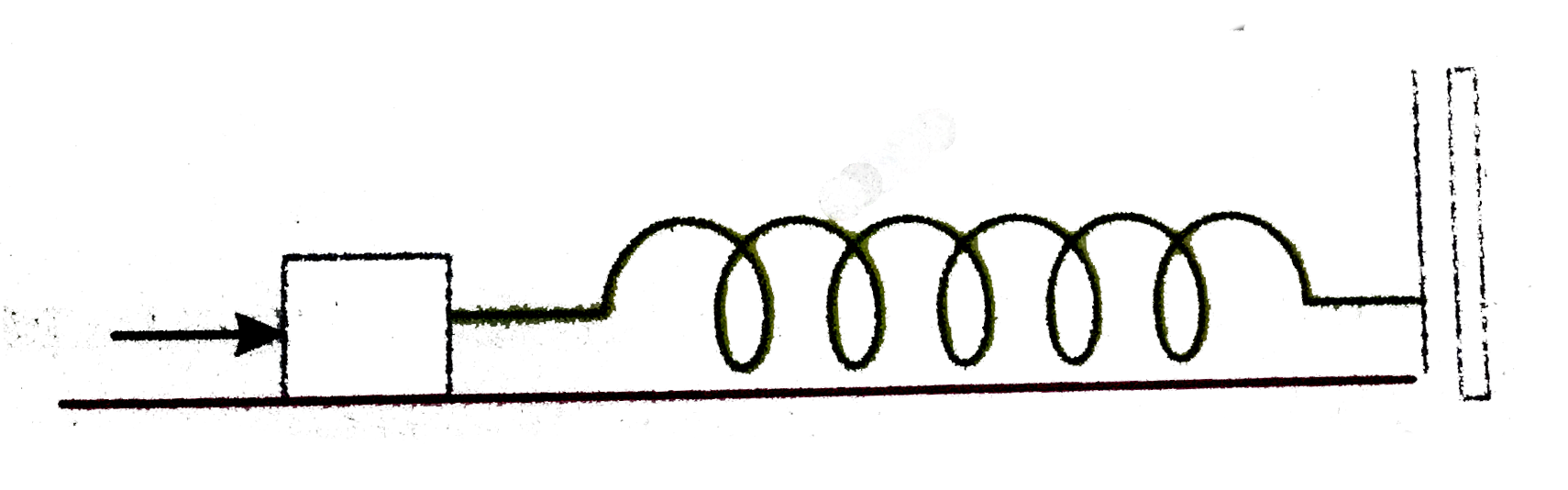 .
.
View SolutionA block of mass 0.18kg is attached to a spring of force constant 2N/m The coefficient of friction between the block and the force is 0.1 insitially its block is at rest and the block as spring is an streched , As impalse is given to the block as shown in the figure . The block sides a distance of 0.06 in and comes to the first time . The initial velocity of the for blocks is mis V=N10 then N is .
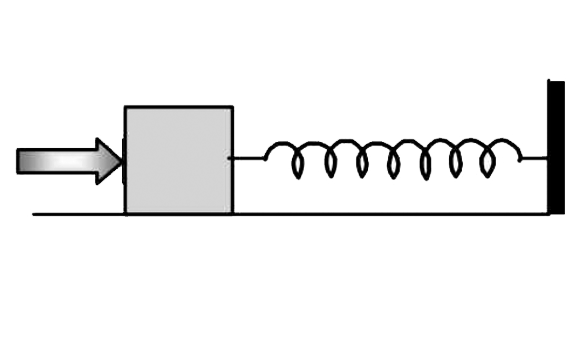
View Solution
Knowledge Check
A block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
A2.5 NB0.98 NC4.9 ND0.49 NA block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness k=100N/m with a velocity 2m/s, the maximum compression of the spring is
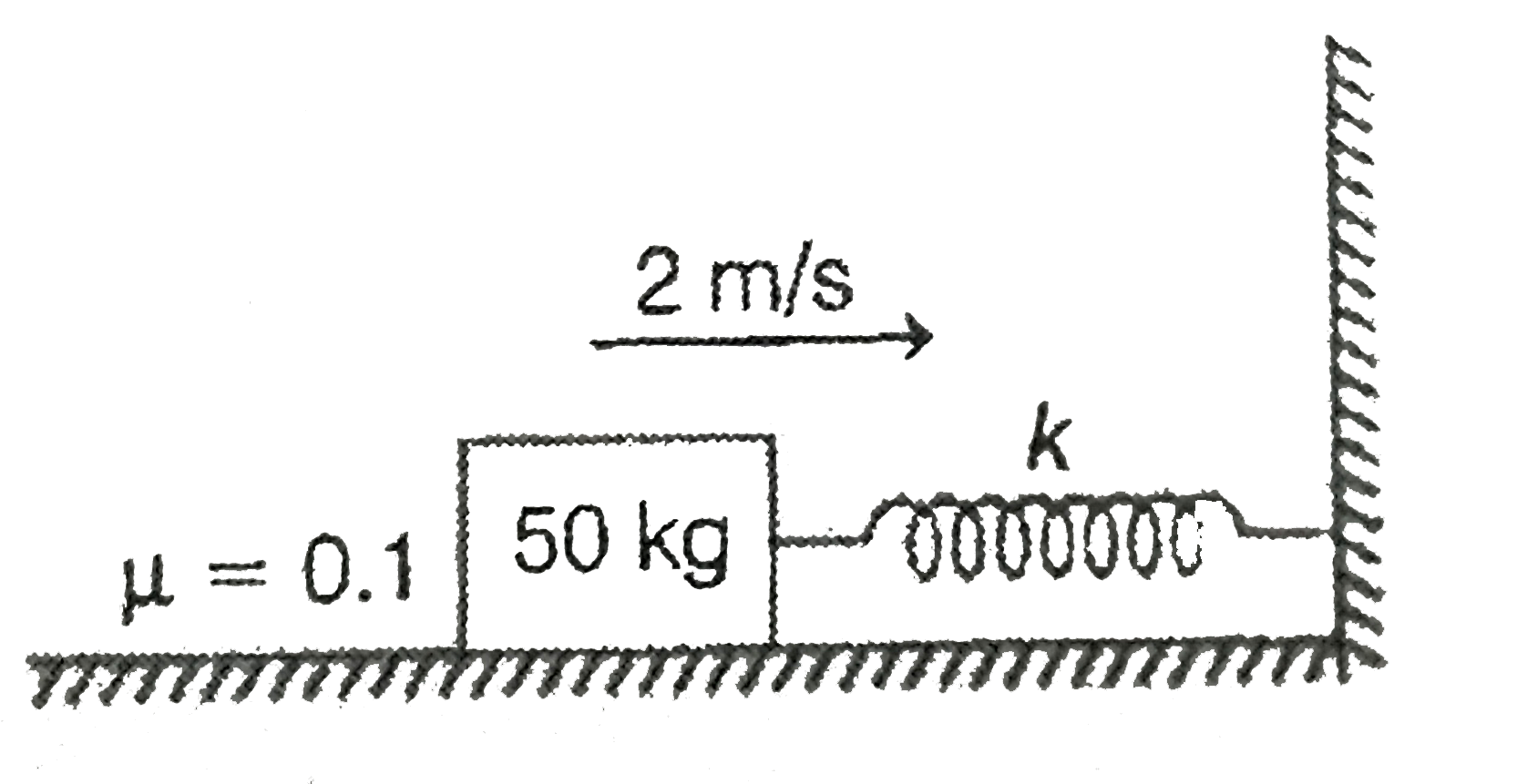 A1 mB2 mC3 mD4 m
A1 mB2 mC3 mD4 mA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
A8.8NB5.8NC2.8ND10.8N
A block of mass 5 kg is pulled along a horizontal. The friction coefficient between the block and the surface is 0.5. If the block travels at constant velocity, find the work done by this applied force during a displacement 4 m of the block.
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of mass 2 kg, initially at rest on a horizontal floor, is now acted upon by a horizontal force of 10N. The coefficient of friction between the block and the floor is 0.2. If g=10m/s2, then :
View SolutionA block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness k=100N/m with a velocity 2m/s, the maximum compression of the spring is
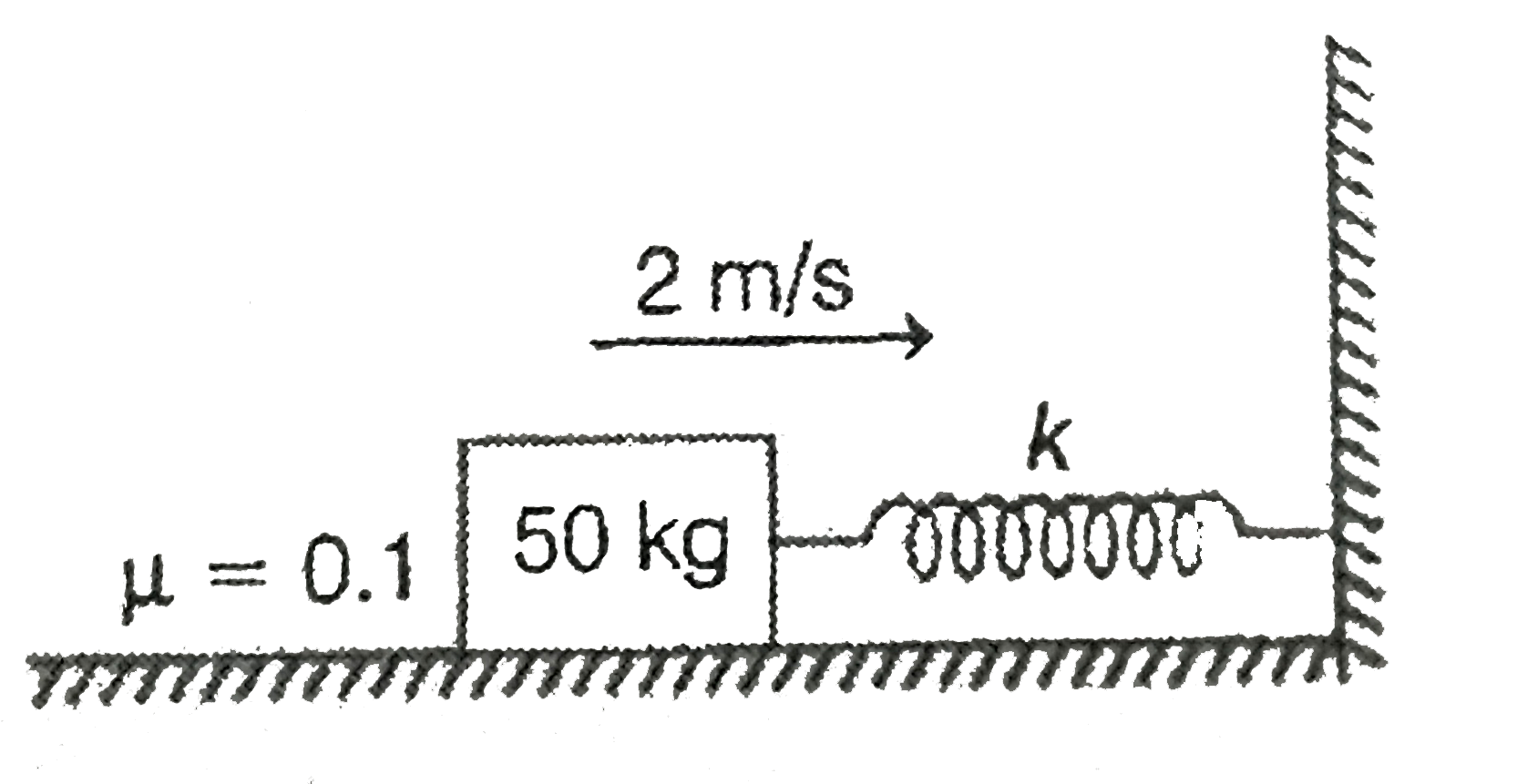
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View Solution
