In figure, block A is released from rest, when spring is at its natural unstretched length. For block B of mass M to leave contact with the ground at some stage, the minimum mass of A must be
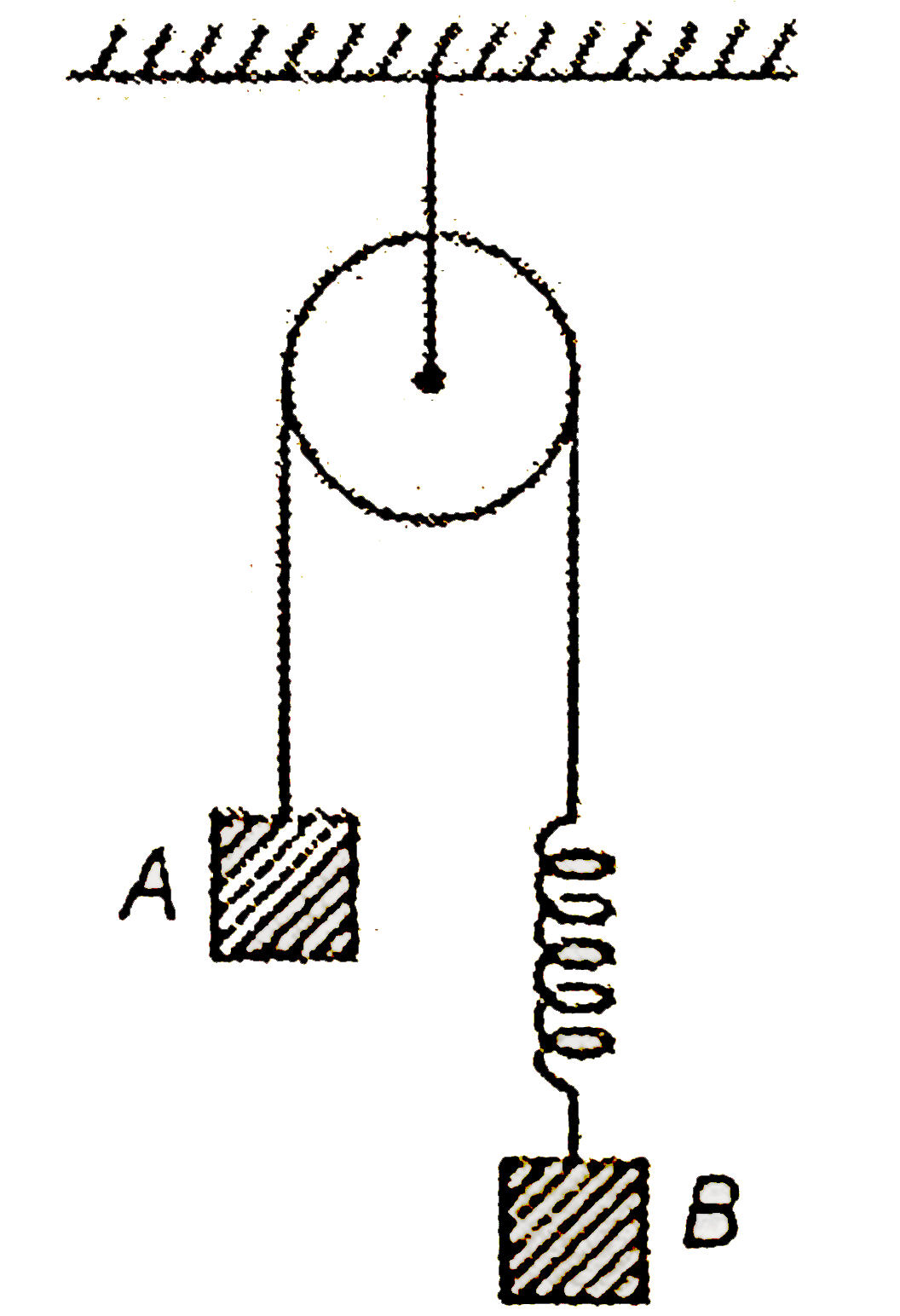
3M
M2
M
cannot say
The correct Answer is:B
The spring will exert maximum force when A is at lowest position, say at distance x from the present position.
∴ mgx=12kx2
where, k is force constant of the spring, for the block B to leave contact, kx = Mg
∴ mgx=12Mgx
∴ m=M2
Topper's Solved these Questions
- NEWTONS LAWS OF MOTION AND FRICTIONBook:BITSAT GUIDEChapter:NEWTONS LAWS OF MOTION AND FRICTIONExercise:BITSAT Archives
Explore 23 Videos
- MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONBook:BITSAT GUIDEChapter:MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONExercise:All Questions
Explore 86 Videos
- ROTATIONAL MOTIONBook:BITSAT GUIDEChapter:ROTATIONAL MOTIONExercise:BITSAT Archives
Explore 9 Videos
Similar Questions
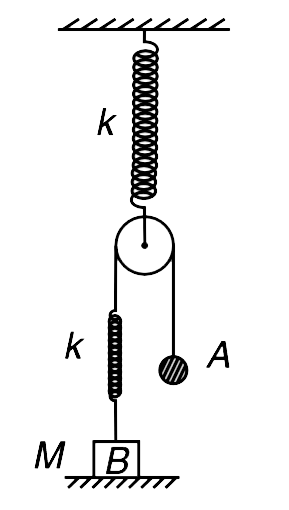
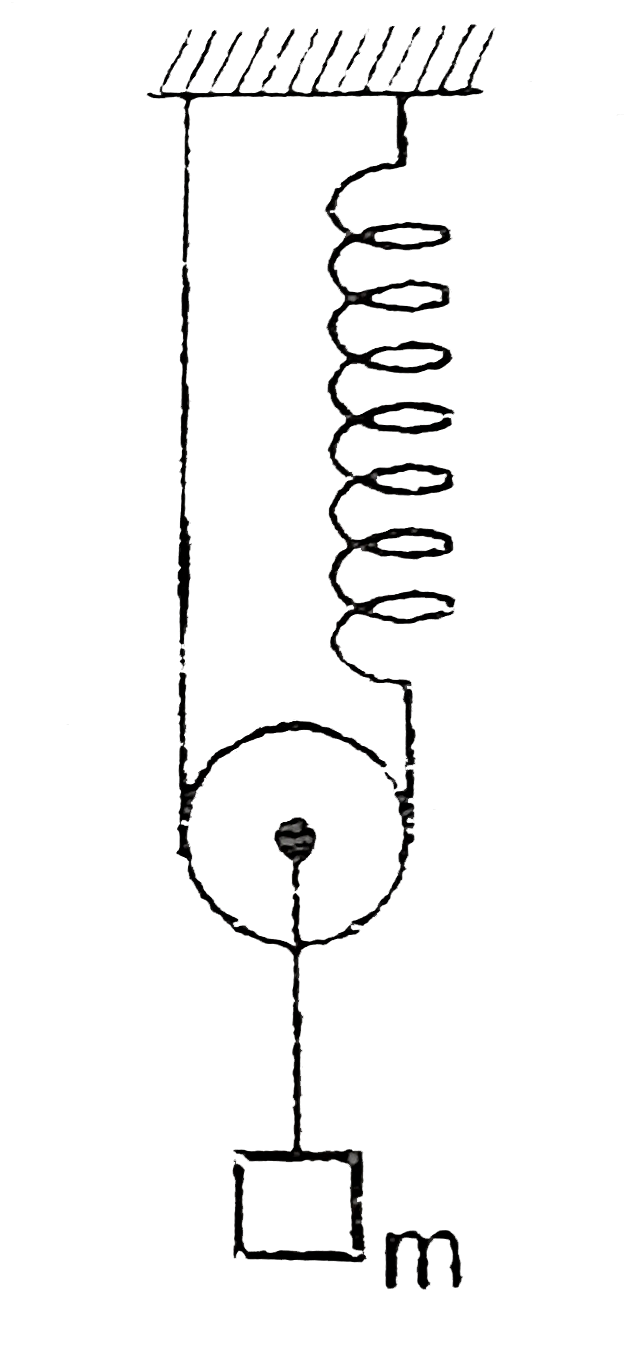
In the arrangement shown in the fig. string, springs and the pulley are mass less. Both the springs have a force constant of k and the mass of block B resting on the table is M. Ball A is released from rest when both the springs are in natural length and just taut. Find the minimum value of mass of A so that block B leaves contact with the table at some stage
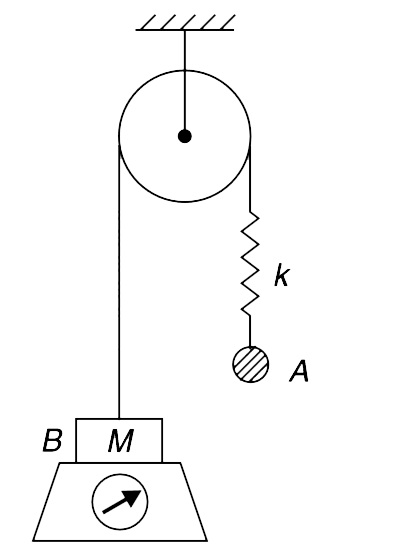
View SolutionIn the arrangement shown in the figure, block B of mass M rests on a weighing scale. Ball A is released from a position where spring is in its natural length and the scale shows the correct weight of block B. Find the mass of ball A so that the minimum reading shown by the scale subsequently is half the true weight of B.
View Solution
Knowledge Check
In the figure, the ball B is released from rest when the spring is in natural length. For the block A of mass 2m to leave contact with the ground at some instant the minimum mass of B must be
 A2mBmCm2Dm4
A2mBmCm2Dm4In the adjoining diagram the ball A is released from rest when the spring is at its natural length (neither stretched nor compressed) For the block B of mass M to leave contact with the ground at some time, the minimum mass of A must be:
 AM2BMC2MDa function of M and force constant k of spring
AM2BMC2MDa function of M and force constant k of springBlock m is released from rest when spring is in its natural length ( assume pulley is ideal and block does not strike on ground during it's motion in vertical plane )
than :
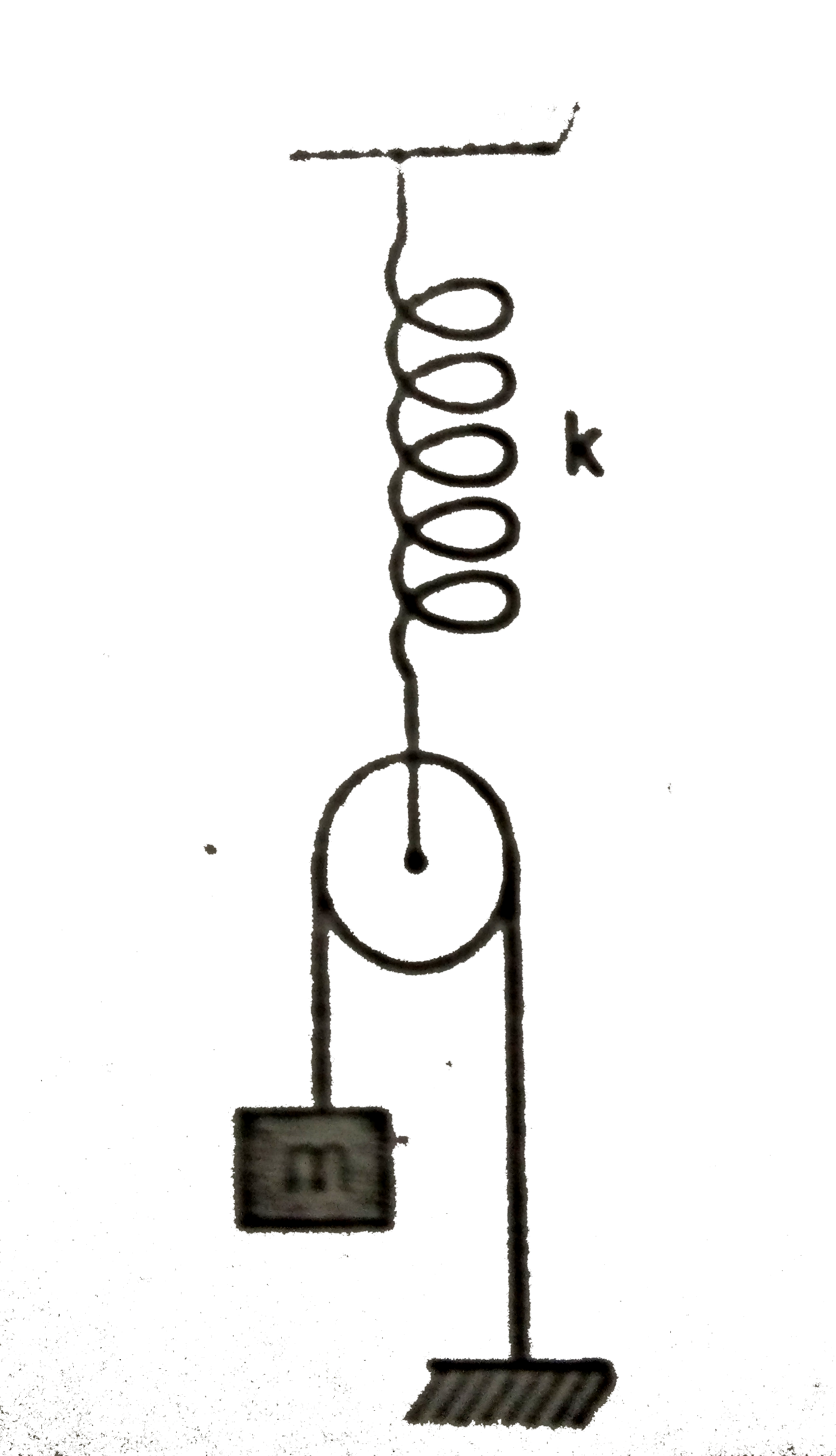 Amaximum elongation in spring is 4mg/kBmaximum elongation in spring is 2mg/kCmaximum speed of block is 2g√mkDmaximum speed of block is g√mk
Amaximum elongation in spring is 4mg/kBmaximum elongation in spring is 2mg/kCmaximum speed of block is 2g√mkDmaximum speed of block is g√mk
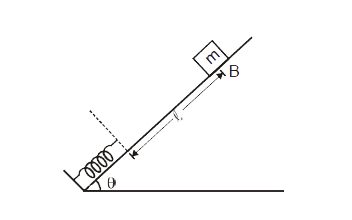
The block shown in figure is released from rest and initially the spring is at its natural length. Write down the energy conservation equation. When the spring is compressed by l1?
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass 'm' is attached to a spring. Block is released from rest, when spring is in natural length. Block is along the pricipal axis of concave mirror and size of block is very small. When spring is in natural length then block is at a distance of 20 cm from the mirror, distance (in cm) in which the image formed by mirror oscillates is (mass of the block =5×10−2 kg, spring constant k=20 N//m)

View SolutionSystem shown in figure is released from rest . Pulley and spring is massless and friction is absent everywhere. The speed of 5kg block when 2kg block leaves the contact with ground is (force constant of spring k=40N/mandg=10m/s2)

View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
View Solution

