In the quadratic equation above, a is a nonzero constant. The graph of the equation in the xy-plane is a parabola with vertex (c,d) . Which of the following is equal to d ?
The correct Answer is:A
To find the value of d in the quadratic equation y=a(x−2)(x+4), we will follow these steps:
Step 1: Identify the Roots
The roots of the quadratic equation can be found by setting y=0:
a(x−2)(x+4)=0
This gives us the roots:
1. x−2=0 → x=2
2. x+4=0 → x=−4
Step 2: Find the x-coordinate of the Vertex
The x-coordinate of the vertex of a parabola can be found by taking the average of the roots:
xvertex=x1+x22=2+(−4)2=−22=−1
Step 3: Substitute x-coordinate into the Equation
Now that we have the x-coordinate of the vertex, we can substitute x=−1 back into the original equation to find d:
y=a(−1−2)(−1+4)
Calculating the values inside the parentheses:
y=a(−3)(3)
Thus,
y=−9a
Step 4: Conclusion
The y-coordinate of the vertex, d, is equal to:
d=−9a
The roots of the quadratic equation can be found by setting y=0:
a(x−2)(x+4)=0
This gives us the roots:
1. x−2=0 → x=2
2. x+4=0 → x=−4
The x-coordinate of the vertex of a parabola can be found by taking the average of the roots:
xvertex=x1+x22=2+(−4)2=−22=−1
Now that we have the x-coordinate of the vertex, we can substitute x=−1 back into the original equation to find d:
y=a(−1−2)(−1+4)
Calculating the values inside the parentheses:
y=a(−3)(3)
Thus,
y=−9a
The y-coordinate of the vertex, d, is equal to:
d=−9a
Similar Questions
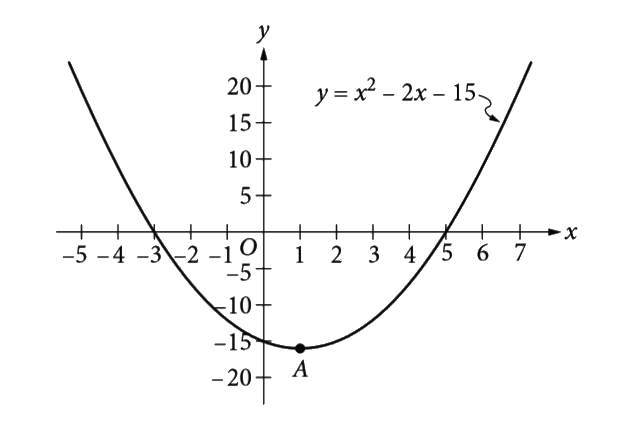
Which of the following is an equivalent form of the equation of the graph shown in the xy-plane above, from which the coordinates of vertex A can be identified as constants in the equation?
View Solutiony=x2−6x+8
The equation above represents a parabola in the xy-plane. Which of the following equivalent forms of the equation displays the x-intercepts of the parabola as constants or coefficients?
View Solutionf(x)=2x+1
The function f is defined by the equation above which of the following is the graph of y=−f(x) in the xy-plane?
View Solutiony=x2−a
In the equation above a is a positive constant and the graph of the equation in the xy-plane is a parabola. Which of the following is an equivalent form of the equation?
View Solution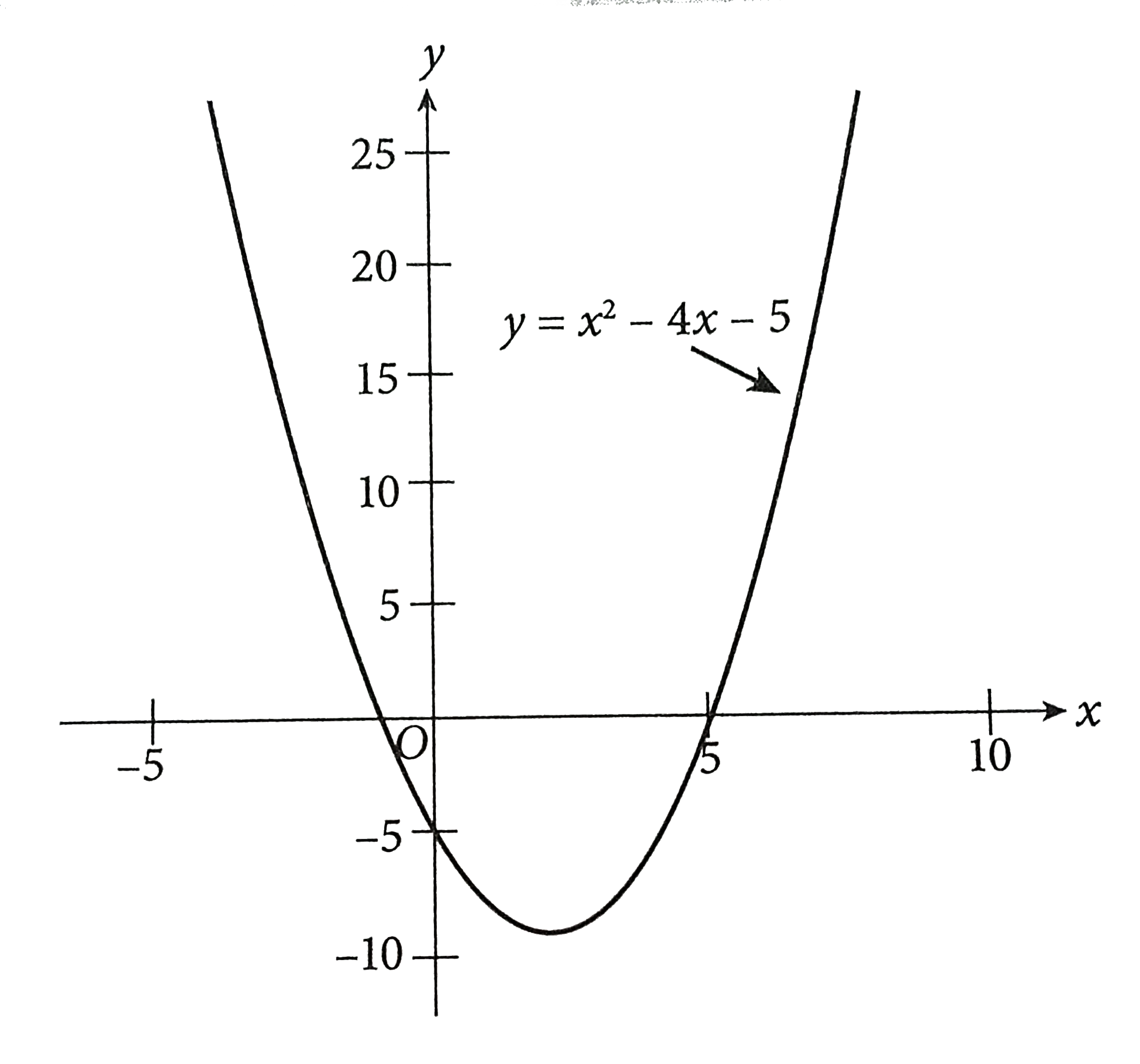
Which of the following is an equivalent form of the equation of the graph shown in the xy plane above, from which the coordinates of vertex Z can be identified as constant in the equation?
View Solution
Which of the following is an equivalent form of the equation of the graph shown in the xy-plane above, from which the coordinates of vertex V can be identified from constants in the equation?
View Solutiony=x2+16x+28
The equation above represents the graph of a parabola in the xy-plane. Which of the following represents an equivalent form of the equation that includes the minimum value of y as a constant?
View Solution
