Figure-5.72 shows a conducting loop of which semi-circular part lies in the magnetic induction B which varies with time, given as
B=at3+ct3+fT
The wire is having a resistance Rω/m. Find current in loop at time t=2s.
Step by step video & image solution for Figure-5.72 shows a conducting loop of which semi-circular part lies in the magnetic induction B which varies with time, given as B=at^(3)+ct^(3)+fT The wire is having a resistance Romega//m. Find current in loop at time t=2s. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Illustration25videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Practice Exercise 5.112videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions389videos
CURRENT ELECTRICITY
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems73videos
ELECTROSTATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The figure shows a current- carrying loop, some part of which is circular and some part is a line segement. The magnetic induction at the centre is
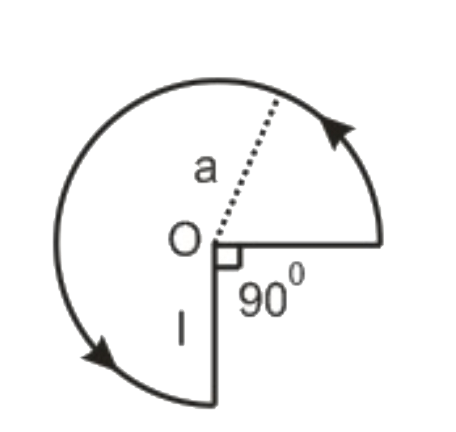A3μ04aBμ0l4πa(1+π)Cμ0l8πaD3μ0l8a - Question 2 - Select One
A plane loop is shaped as two squares (Fig) and placed in a uniform magnetic field at right angle to the loop's plane. The magnetic induction varies with time as B=B0sin(ω)t,whereB0=10mTand(ω)=100rads−1. The wires do not touch at point A. If resistance per unit length of the loop is 50m(Ω)/m, then amplitude of current induced in the loop is
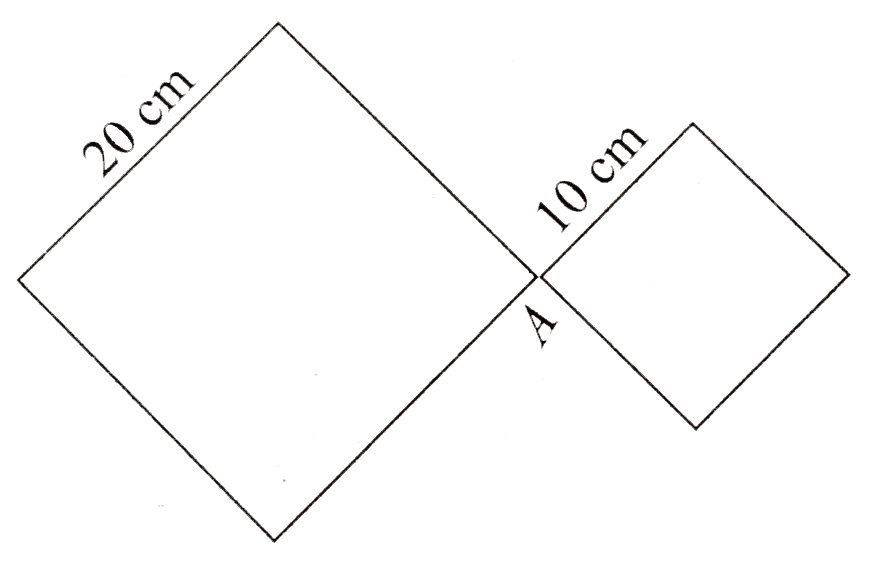A1.5AB1.0AC0.5AD2.0A - Question 3 - Select One
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of ring. If radius R varies as a function of time t as R=R0+t2. The emf induced in the loop is
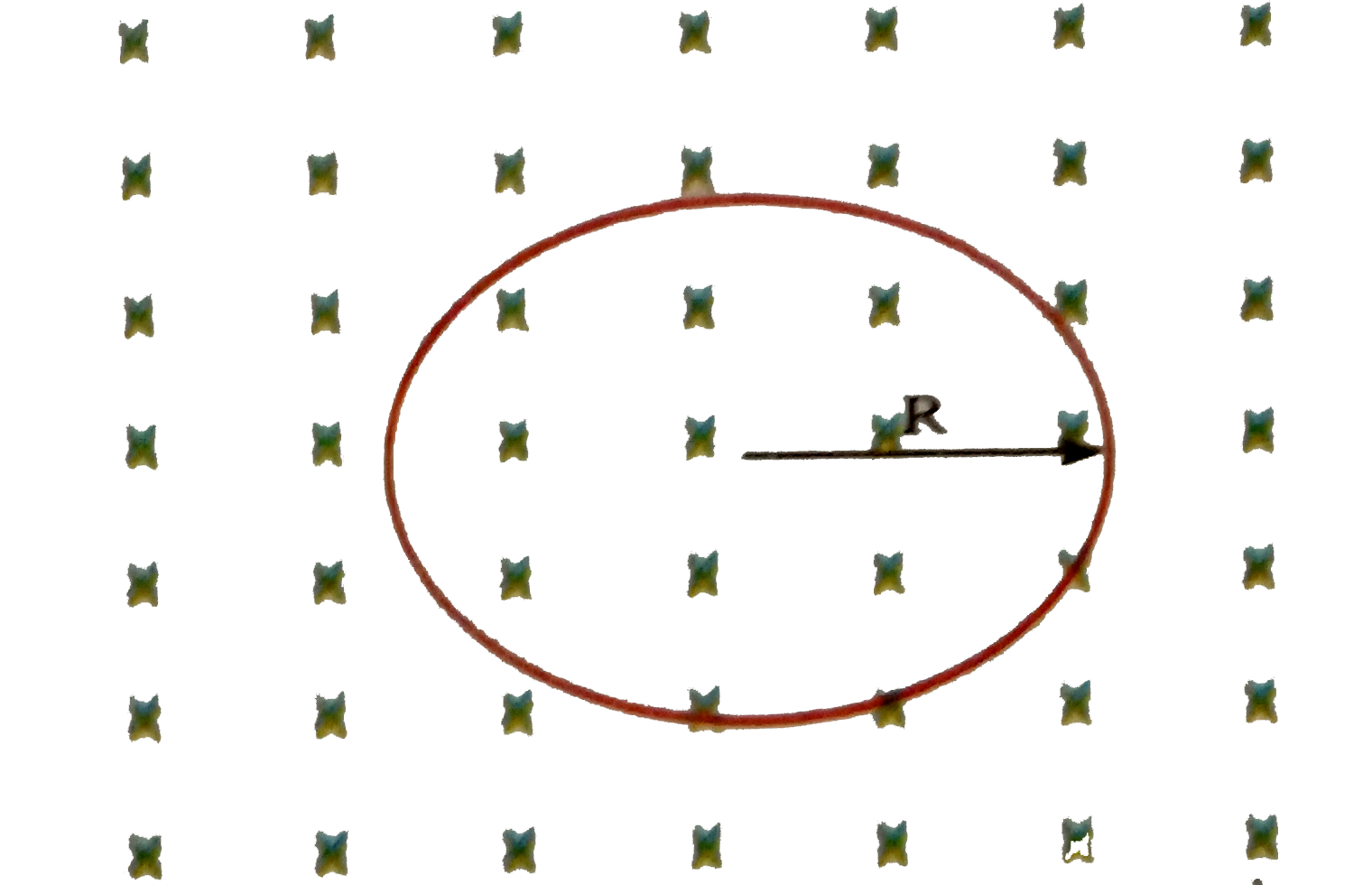A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
A circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
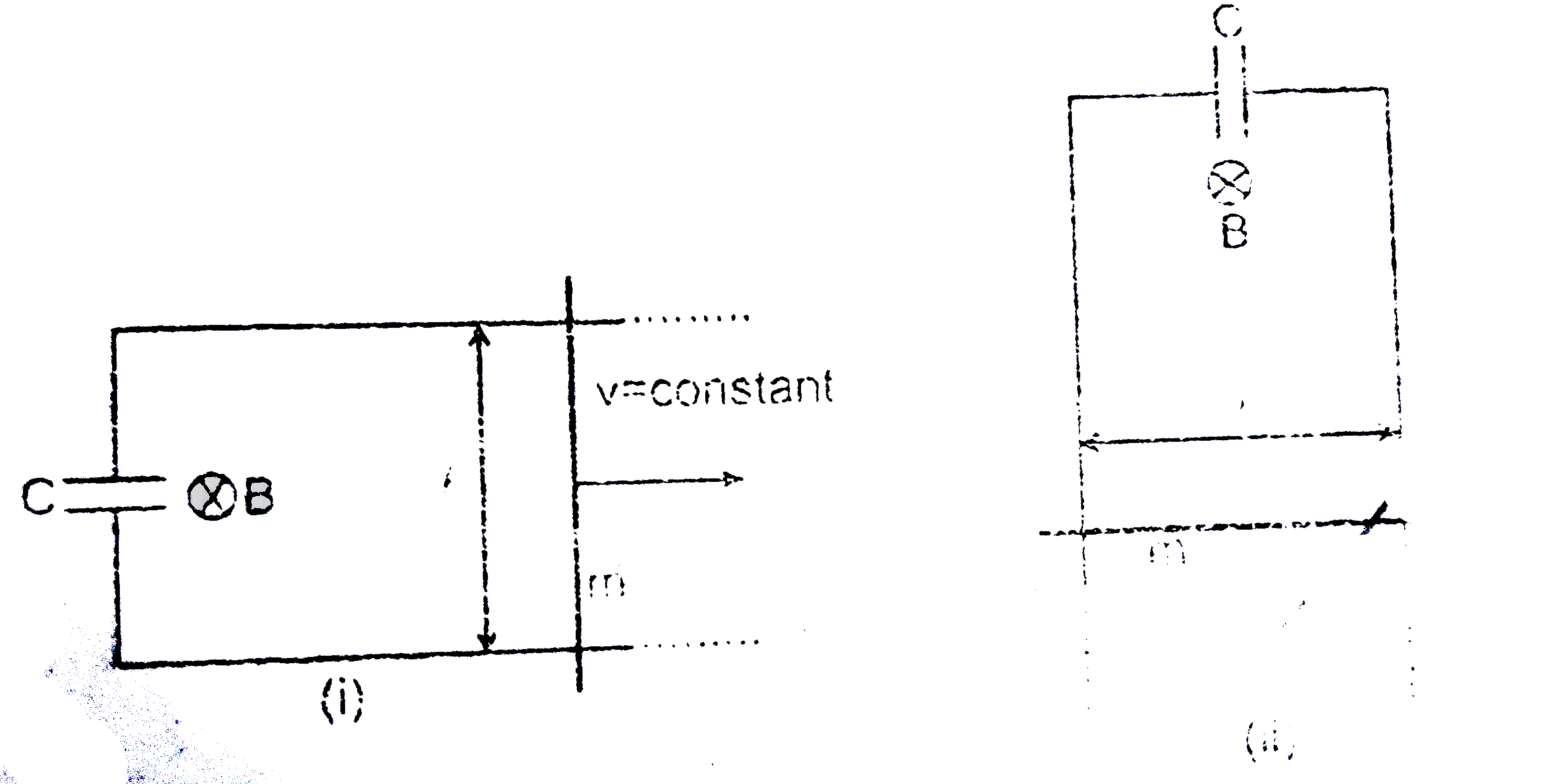
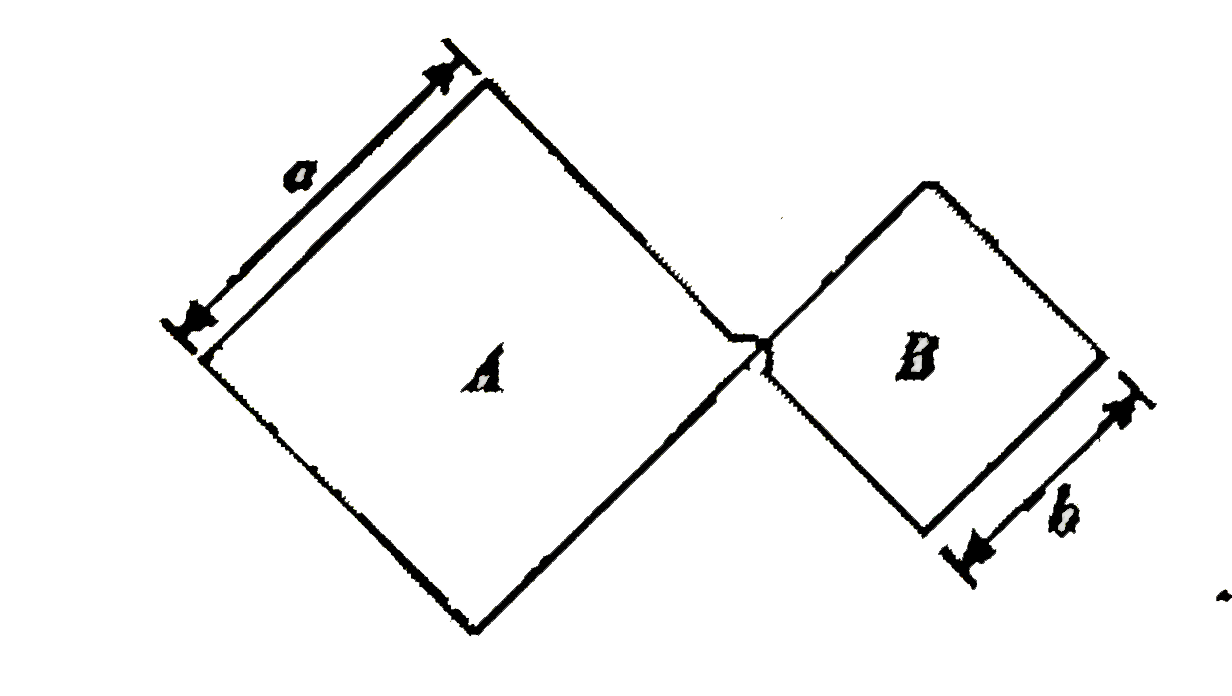
View SolutionA plane loop shown in figure-5.71 is shaped in the from of two squares with sides a and b and it is introduced into a uniform magnetic field at right angles, to the loop's plane. The magnetic induction varies with time as B=B0sinωt. find the amplitude of the current induced in the loop if its resistance per unit length is equal to r. the induction of the loop is negligible.
View SolutionA super conducing loop having an inductance L is kept in a magnetic field which is varying with respect to time. If ϕ is the total flux, ε=total induced emf, then:
View Solution