There are two stationary loops with mutual inductance . The current is one of the loops starts to be varied as where is a current, is time. Find the time dependence of the current in the other loop whose inductance is and resistance .
Step by step video & image solution for There are two stationary loops with mutual inductance L_(12). The current is one of the loops starts to be varied as I_(1) = alpha t where alpha is a current, t is time. Find the time dependence I_(2) (t) of the current in the other loop whose inductance is L_(2) and resistance R. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Practice Exercise 5.1
12 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Practice Exercise 5.2
14 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
Similar Questions
If the current in the ineer loop changes according to i=2t2 then, find the current in the capacitor as a function of time.

View SolutionA square loop of side length d has a capacitor of capacitance C and the resistance of the loop is R. In the plane of the loop there is a long straight current carrying wire having current I. The distance of the straight wire from the loop is d as shown in figure. The current in the straight wire is made to grow with time as I=αt where α=2As−1. Neglect self inductance of the loop.
(a) Find the charge on the capacitor as a function of time (t).
(b) Find the heat generated in the loop as a function of time.
(c) Who supplies energy for heat dissipation?
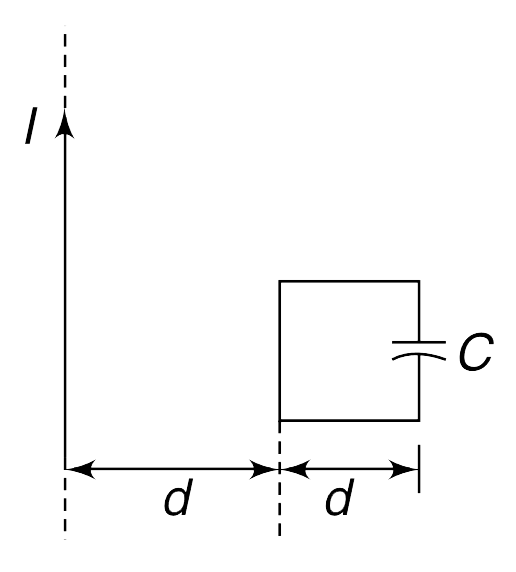
View Solution
Knowledge Check
In Fig, the mutual inductance of a coil and a very long straight wire is M, coil has resistance R and self-inductance L. The current in the wire varies according to the law I=at, where a is a constant and t is the time, the time dependence of current in the coil is
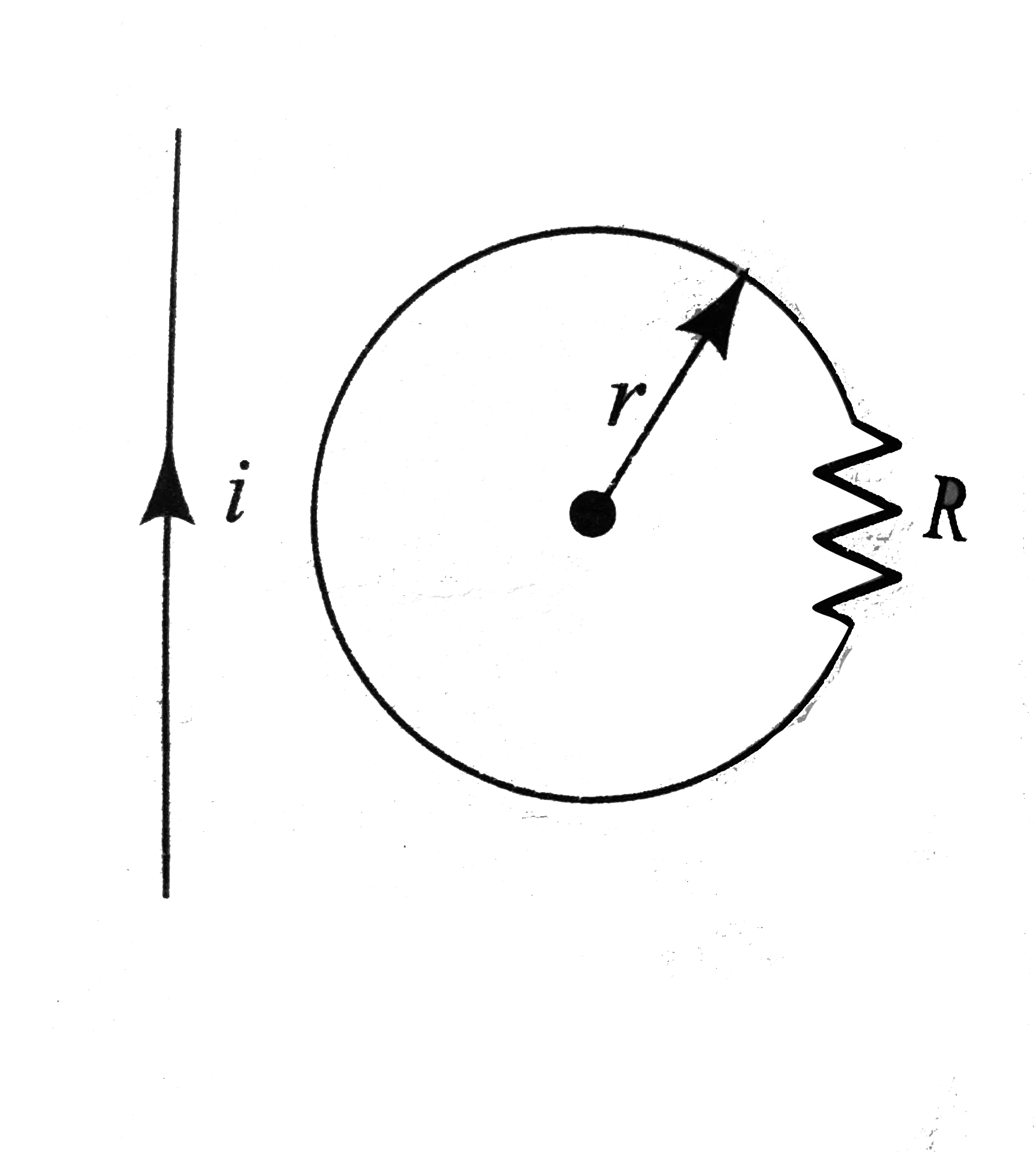 AMaRBmaRe−Rt/LCMRe−tR/LDMaR(1−e−tR/L)
AMaRBmaRe−Rt/LCMRe−tR/LDMaR(1−e−tR/L)In the adjacent figure, the mutual inducatance of the infinite straight wire and the coil is M, while the self inductance of the coil is L. The current in infinite wire is varying according to the realtion l1=αt, where α is a constant and t is the time. The time dependence of current in the coil is
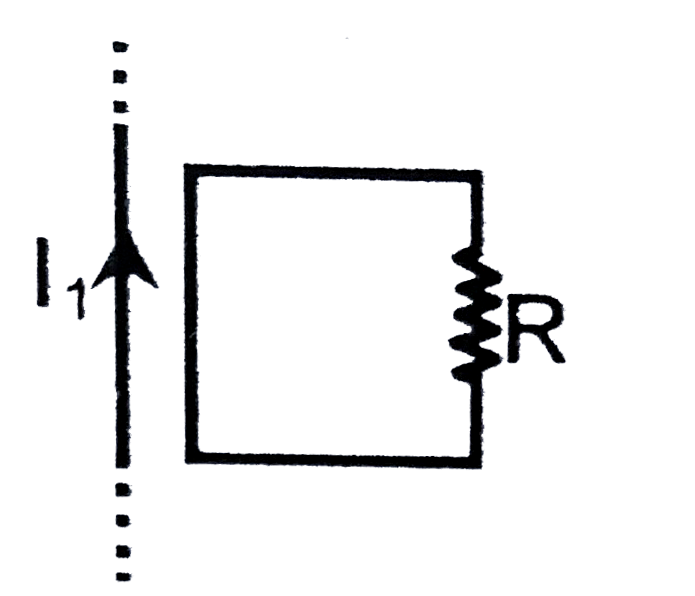 AMαRBMαLRe−Rt/LCαR(1−e−Rt/L)Dnone of these
AMαRBMαLRe−Rt/LCαR(1−e−Rt/L)Dnone of theseThe current in an L - R circuit in a time t = 2L / R reduces to-
A336.5% of maximumB13.5% of maximumC0.50% of maximumD63.2% of maximum
If the current in the inner loop changes according to I=2t2 (Fig .), then find the current in the capacitor as a function of time.

View SolutionTwo different wire loops are concentric and lie in the same plane. The current in the outer loop (I) is clockwise and increases with time. The induced current in the inner loop

View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View SolutionA current through a wire depends on time as i=α0t+βt2 where α0=20A/s and β=8As−2 . Find the charge crossed through a section of the wire in 15 s.
View SolutionThe magnetic flux through a stationary loop with resistance R varies during interval of time T as ϕ = at (T – t). The heat generated during this time neglecting the inductance of loop will be
View Solution
