In an LR-circuit the current attains one-third of its final steady value in 5s. What is the time-constant of the circuit ?
The correct Answer is:12.3s
To solve the problem, we need to find the time constant (τ) of an LR circuit where the current reaches one-third of its final steady value in 5 seconds.
1. Understand the Current Growth in an LR Circuit:
The current I(t) in an LR circuit can be described by the equation:
I(t)=I0(1−e−tτ)
where I0 is the final steady value of the current, t is the time, and τ is the time constant.
2. Set Up the Equation for One-Third of Final Value:
According to the problem, the current attains one-third of its final steady value in 5 seconds. Therefore, we can write:
I(5)=I03
Substituting into the equation gives:
I03=I0(1−e−5τ)
3. Simplify the Equation:
Dividing both sides by I0 (assuming I0≠0):
13=1−e−5τ
Rearranging this gives:
e−5τ=1−13=23
4. Take the Natural Logarithm:
Taking the natural logarithm of both sides:
−5τ=ln(23)
This can be rewritten as:
5τ=−ln(23)
5. Use the Given Value of ln(2):
We know from the problem that ln(2)=0.405. We can express ln(23) as:
ln(23)=ln(2)−ln(3)
Since ln(3) can be approximated using ln(3)≈1.099 (not provided in the question, but can be found), we can calculate:
ln(23)≈0.405−1.099=−0.694
6. Calculate the Time Constant τ:
Substituting back into the equation gives:
5τ=0.694
Therefore:
τ=50.694≈7.21 seconds
Final Answer:
The time constant τ of the circuit is approximately 7.21 seconds.
The current I(t) in an LR circuit can be described by the equation:
I(t)=I0(1−e−tτ)
where I0 is the final steady value of the current, t is the time, and τ is the time constant.
According to the problem, the current attains one-third of its final steady value in 5 seconds. Therefore, we can write:
I(5)=I03
Substituting into the equation gives:
I03=I0(1−e−5τ)
Dividing both sides by I0 (assuming I0≠0):
13=1−e−5τ
Rearranging this gives:
e−5τ=1−13=23
Taking the natural logarithm of both sides:
−5τ=ln(23)
This can be rewritten as:
5τ=−ln(23)
We know from the problem that ln(2)=0.405. We can express ln(23) as:
ln(23)=ln(2)−ln(3)
Since ln(3) can be approximated using ln(3)≈1.099 (not provided in the question, but can be found), we can calculate:
ln(23)≈0.405−1.099=−0.694
Substituting back into the equation gives:
5τ=0.694
Therefore:
τ=50.694≈7.21 seconds
The time constant τ of the circuit is approximately 7.21 seconds.
Topper's Solved these Questions
- TRANSIENT CURRENTBook:SL ARORAChapter:TRANSIENT CURRENTExercise:Example
Explore 37 Videos
- TRANSIENT CURRENTBook:SL ARORAChapter:TRANSIENT CURRENTExercise:Type A
Explore 22 Videos
- TRANSIENT CURRENTBook:SL ARORAChapter:TRANSIENT CURRENTExercise:Type D
Explore 13 Videos
- THERMOELECTRICITYBook:SL ARORAChapter:THERMOELECTRICITYExercise:Problems for Self Practice
Explore 13 Videos
- UNIVERSEBook:SL ARORAChapter:UNIVERSEExercise:PROBLEM_TYPE
Explore 6 Videos
Similar Questions
Knowledge Check
The current in an L−R circuit builds upto 3/4th of its steady state value in 4sec. Then the time constant of this circuit is
A1ln2secB3ln2secC4ln2secD2ln2secThe current in a LR circuit builds up to 34th of its steady state value in 4s . The time constant of this circuit is
A1ln2sB2ln2sC3ln2sD4ln2sThe current in a LR circuit builds up to 34th of its steady state value ion 4s. The time constant of this circuit is
A1in2sB2in2sC3in2sD4In2s
The current in an RL circuit builds up to one-third of its steady-state value in 5.00 s. Find the inductive time constant.
View SolutionThe value of time constant for given circuit is …………s
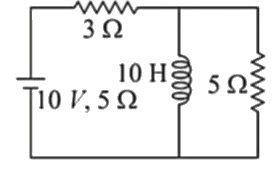
View SolutionIn an LR circuit, current at t=0 is 20A. After 2s it reduces to 18A. The time constant of the circuit is :
View SolutionIn an LR circuit, current at t=0 is 2A . After 2s it reduced to 18A. The time constant of the circuit is (in second)
View SolutionWhen a choke coil carrying a steady current is short circuited, the current in it decreases to β(<1) times its initial value in a time T. The time constant of the choke coil is
View Solution

