Current in an LR circuit attains one-fourth of its steady state value in 2 seconds. Calculate time constant for this circuit.
To solve the problem of finding the time constant of an LR circuit where the current attains one-fourth of its steady state value in 2 seconds, we can follow these steps:
Step 1: Understand the current growth in an LR circuit
The current I(t) in an LR circuit as a function of time is given by the equation:
I(t)=I0(1−e−tτ)
where I0 is the steady state current, τ is the time constant, and t is the time.
Step 2: Set up the equation for the given condition
According to the problem, at t=2 seconds, the current I(2) is one-fourth of the steady state current I0:
I(2)=I04
Substituting this into the equation gives:
I04=I0(1−e−2τ)
Step 3: Simplify the equation
We can divide both sides by I0 (assuming I0≠0):
14=1−e−2τ
Rearranging this gives:
e−2τ=1−14=34
Step 4: Take the natural logarithm
Taking the natural logarithm of both sides:
−2τ=ln(34)
This can be rewritten as:
2τ=−ln(34)
Step 5: Solve for the time constant τ
Now, we can solve for τ:
τ=2−ln(34)
Step 6: Calculate the numerical value
Using the property of logarithms:
−ln(34)=ln(43)
Thus, we have:
τ=2ln(43)
Final Answer
The time constant τ for the circuit is:
τ=2ln(43) seconds
The current I(t) in an LR circuit as a function of time is given by the equation:
I(t)=I0(1−e−tτ)
where I0 is the steady state current, τ is the time constant, and t is the time.
According to the problem, at t=2 seconds, the current I(2) is one-fourth of the steady state current I0:
I(2)=I04
Substituting this into the equation gives:
I04=I0(1−e−2τ)
We can divide both sides by I0 (assuming I0≠0):
14=1−e−2τ
Rearranging this gives:
e−2τ=1−14=34
Taking the natural logarithm of both sides:
−2τ=ln(34)
This can be rewritten as:
2τ=−ln(34)
Now, we can solve for τ:
τ=2−ln(34)
Using the property of logarithms:
−ln(34)=ln(43)
Thus, we have:
τ=2ln(43)
The time constant τ for the circuit is:
τ=2ln(43) seconds
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:NCERT FILE (NCERT TEXTBOOK EXERCISE)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:NCERT FILE (NCERT ADDITIONAL EXERCISE)
Explore 7 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CONCEPTUAL QUESTIONS
Explore 22 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Chapter Practice Test
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
Knowledge Check
The current in an L−R circuit builds upto 3/4th of its steady state value in 4sec. Then the time constant of this circuit is
A1ln2secB3ln2secC4ln2secD2ln2secThe current in a LR circuit builds up to 34th of its steady state value ion 4s. The time constant of this circuit is
A1in2sB2in2sC3in2sD4In2sThe current in a LR circuit builds up to 34th of its steady state value in 4s . The time constant of this circuit is
A1ln2sB2ln2sC3ln2sD4ln2s
The current in an RL circuit builds up to one-third of its steady-state value in 5.00 s. Find the inductive time constant.
View SolutionThe current in a discharging LR circuit without the battery drops from 2.0 A to 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?
View SolutionAnalyse the circuit shown in the figure in steady state
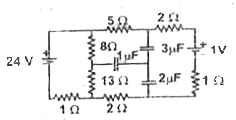
View SolutionThe value of time constant for the given circuit is
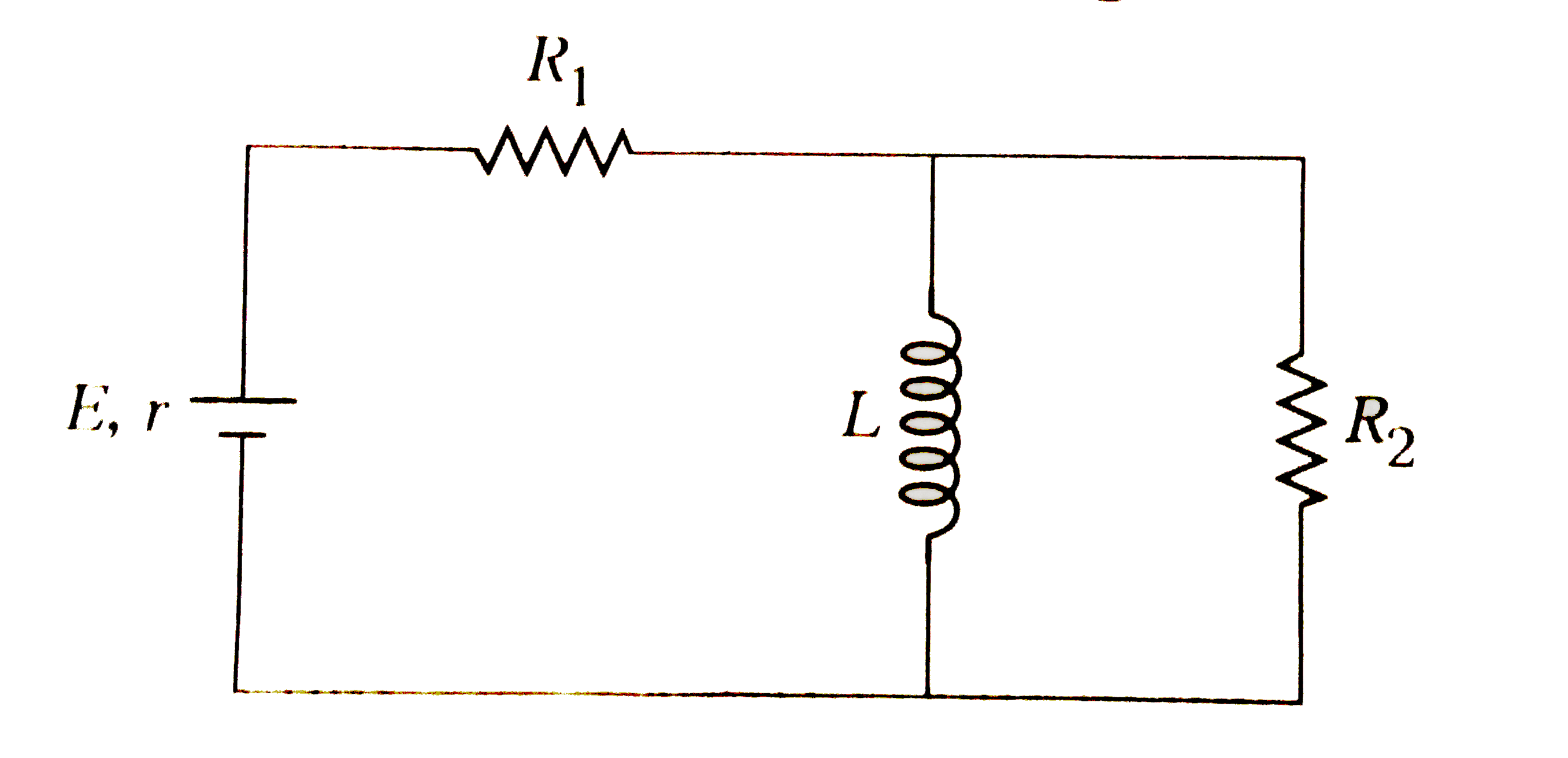
View SolutionTime constant of LR circuit will be
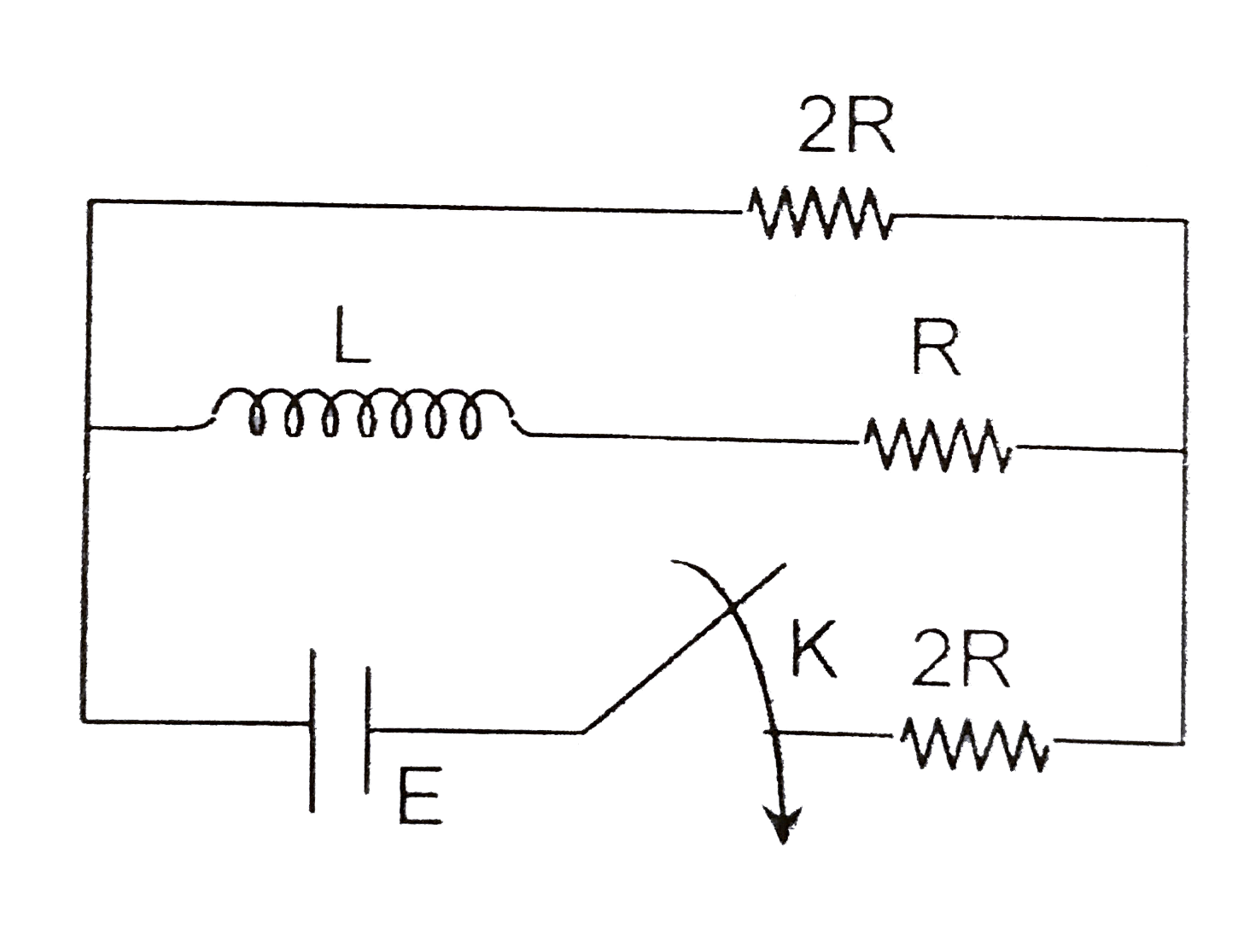
View Solution