A spool of mass M and radius 2R lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. The value of m so that system is in equilibrium is
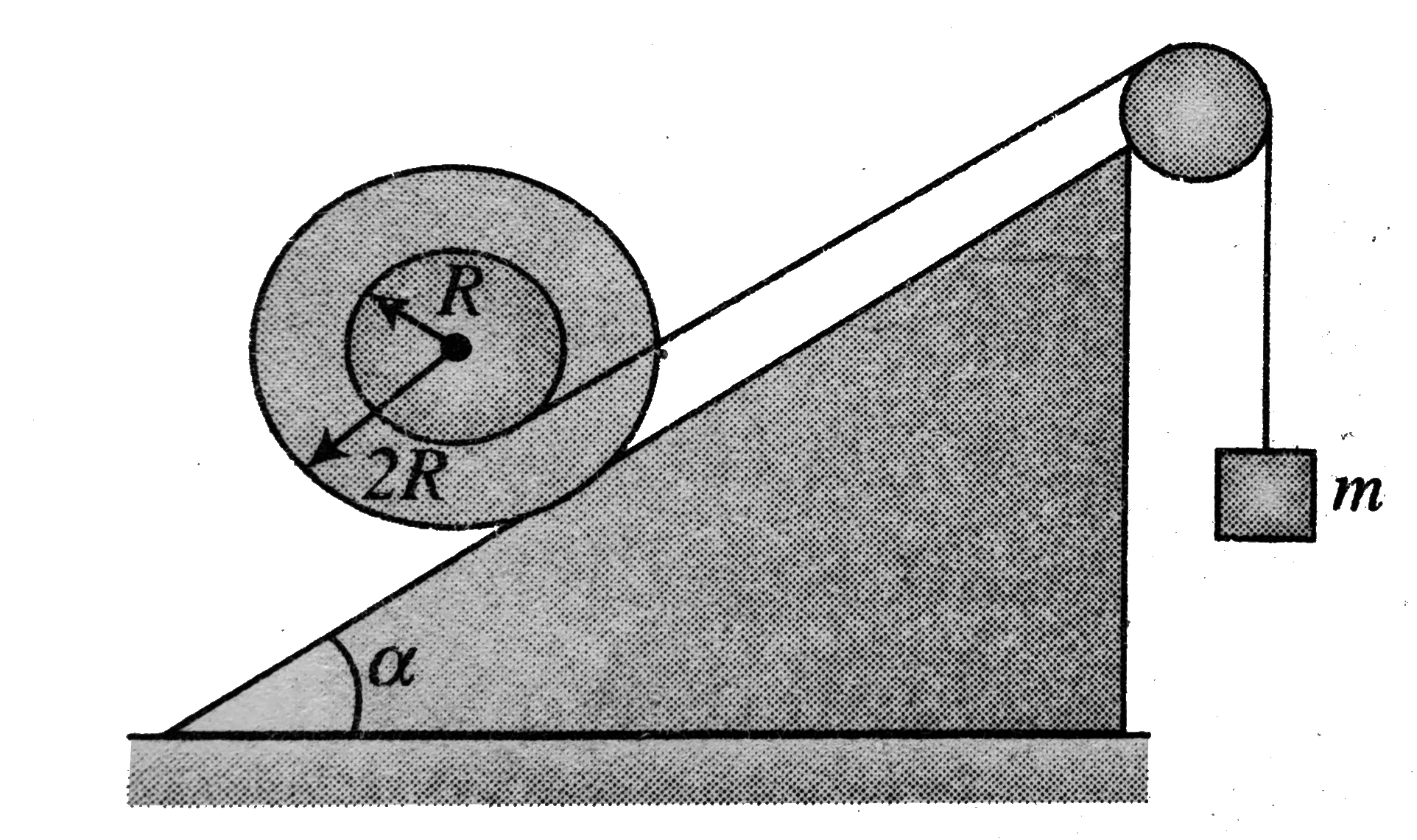
2Msinα
Msinα
2Mtanα
Mcosα
The correct Answer is:A
Step by step video, text & image solution for A spool of mass M and radius 2R lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. The value of m so that system is in equilibrium is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:More than one option is correct
Explore 36 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Comprehension Type Questions
Explore 41 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
Similar Questions
Knowledge Check
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
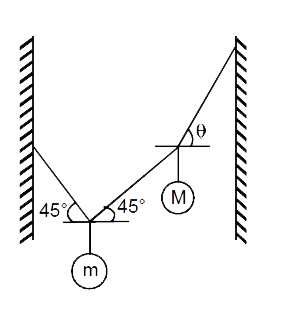 Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


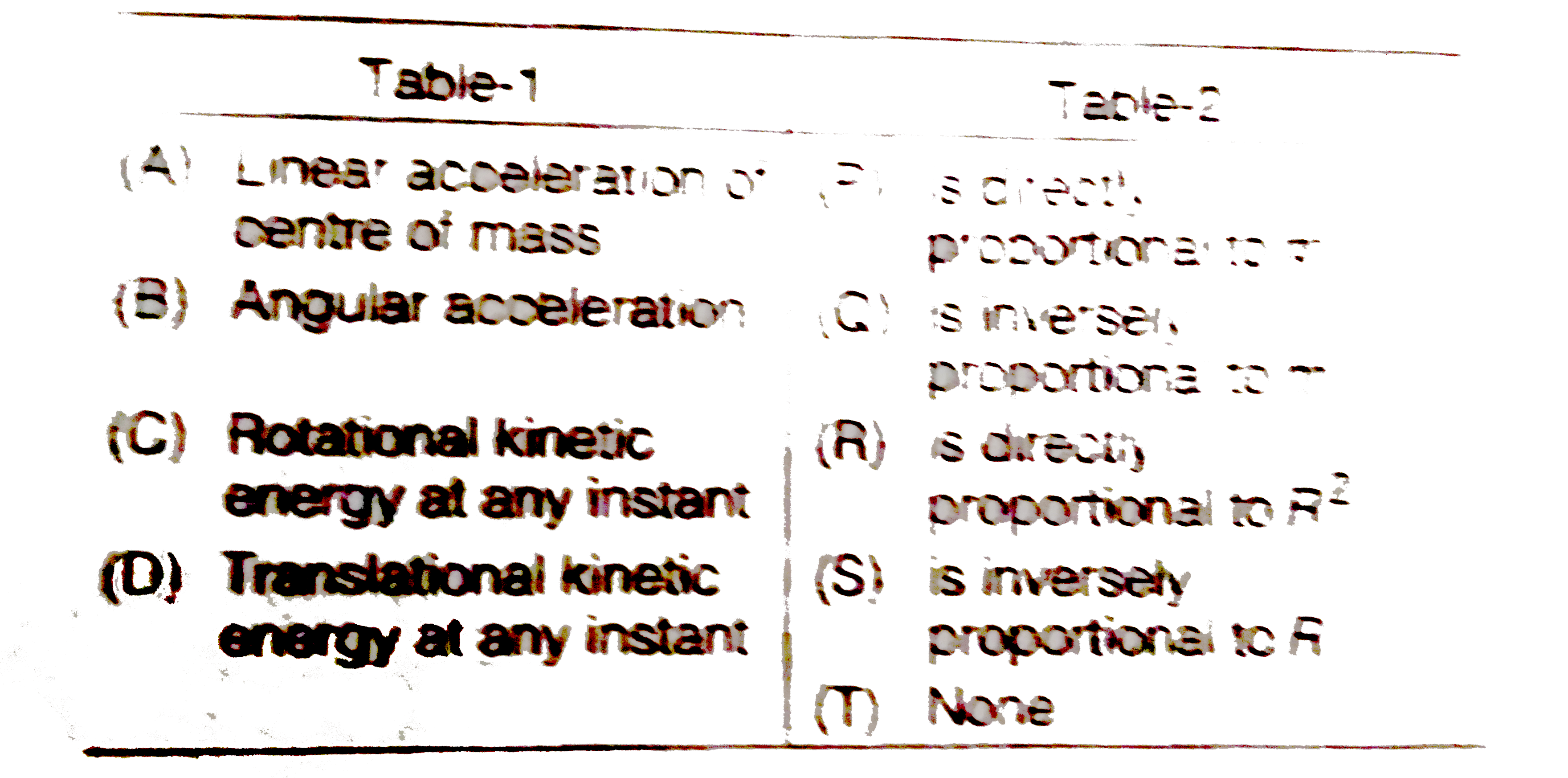
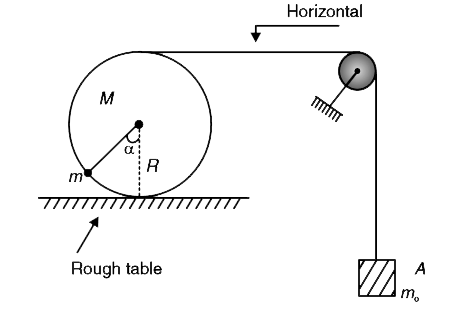
View SolutionA hollow cylindrical pipe of mass M and radius R has a thin rod of mass m welded inside it, along its length. A light thread is tightly wound on the surface of the pipe. A mass m0 is attached to the end of the thread as shown in figure. The system stays in equilibrium when the cylinder is placed such that α=30∘ The pulley shown in figure is a disc of mass M2
(a) Find the direction and magnitude of friction force acting on the cylinder.
(b) Express mass of the rod ‘m’ in terms of m0
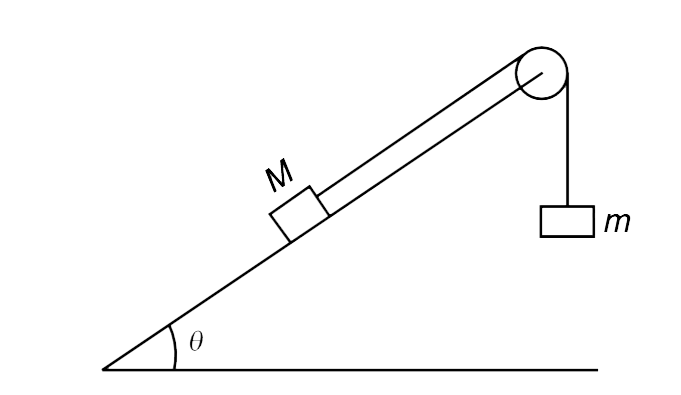
View SolutionA particle of mass M rests on a rough inclined plane at an angle q to the horizontal(sinθ=45). It is connected to another mass m as shown in fig. The pulley and string are light. The largest value of m for which equilibrium is possible is M. Find the smallest value of m for which equilibrium is possible
View SolutionA spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.

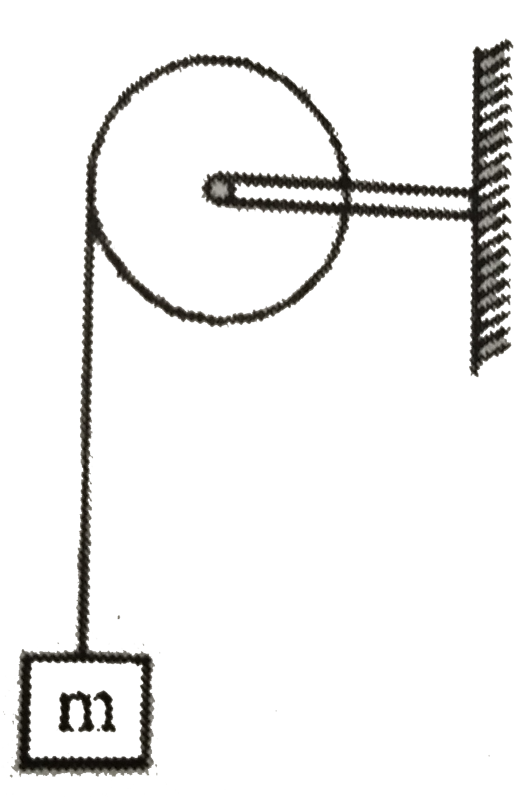
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
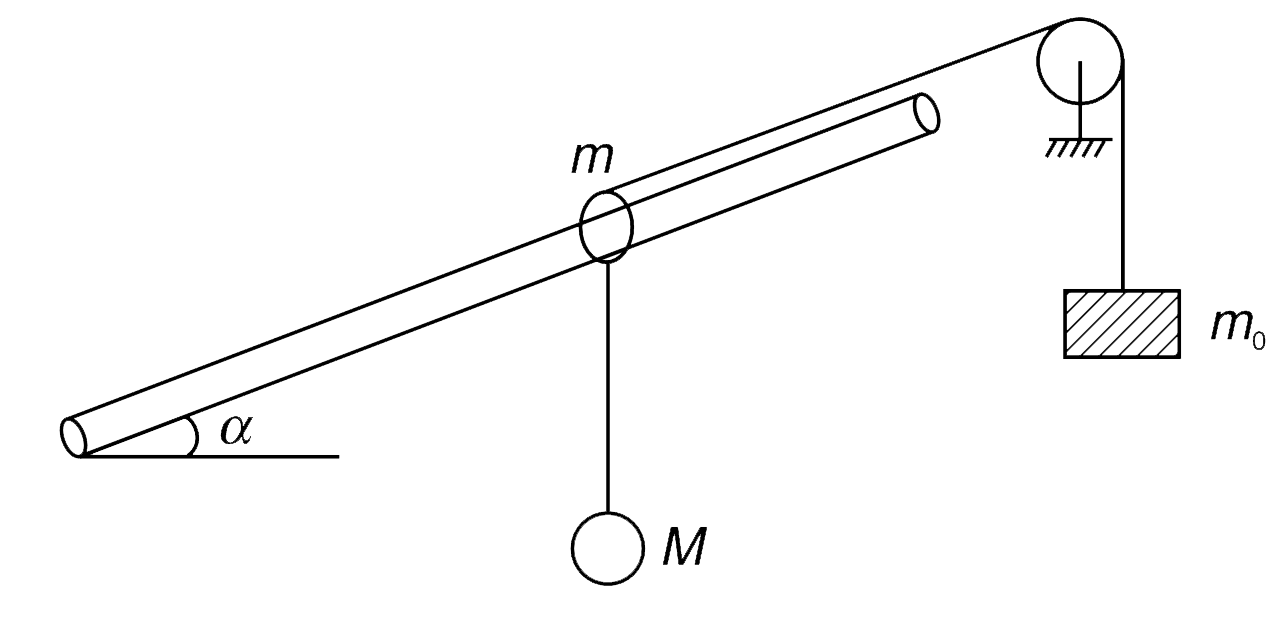
View SolutionA smooth rod is fixed at an angle α to the horizontal. A small ring of mass m can slide along the rod. A thread carrying a small sphere of mass M is attached to the ring. To keep the system in equilibrium, another thread is attached to the ring which carries a load of mass m0at its end (see figure). The thread runs parallel to the rod between the ring and the pulley. All threads and pulley are massless.
(a) Find m0 so that system is in equilibrium.
(b) Find acceleration of the sphere M immediately after the thread supporting m0 is cut.
View Solution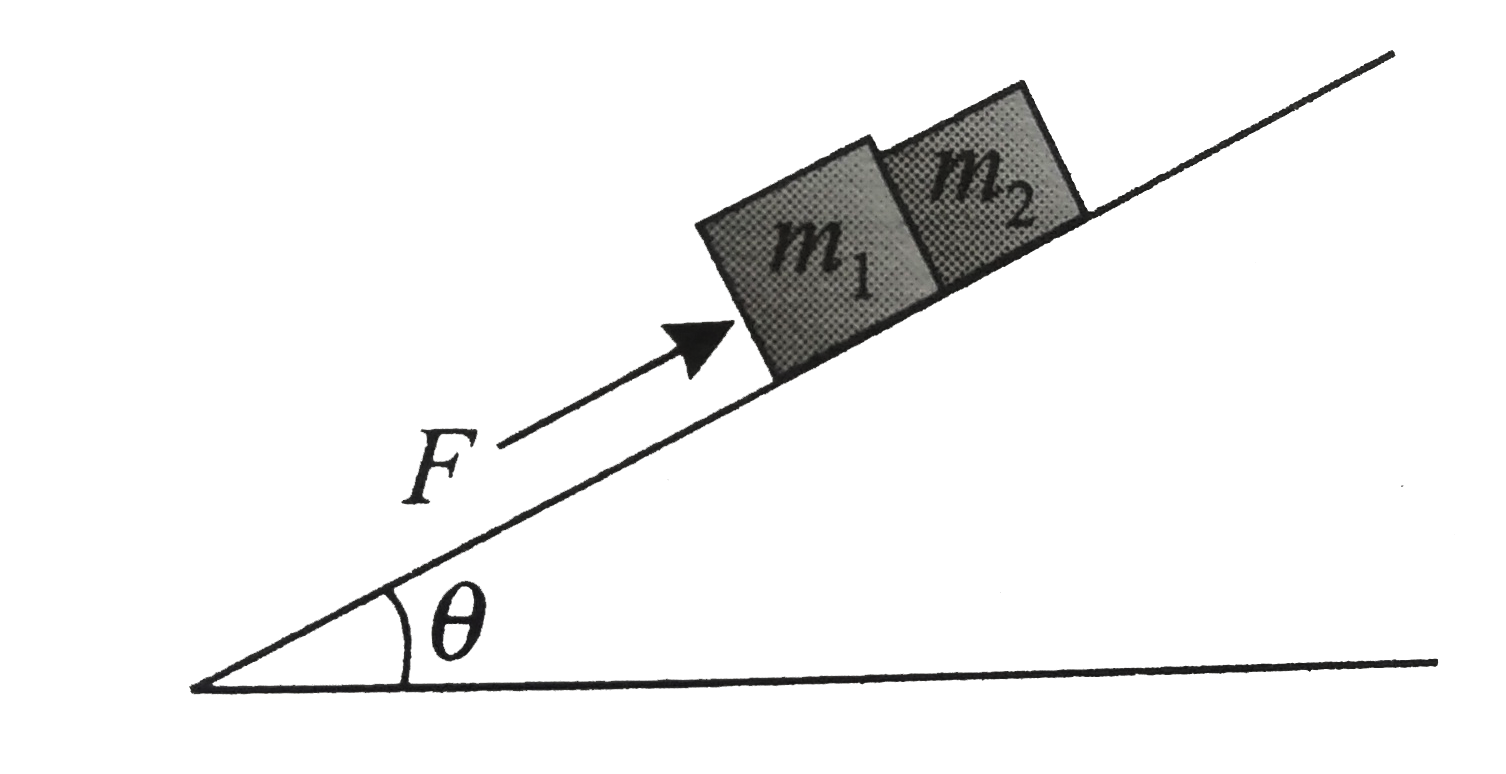
Two blocks are placed at rest on a smooth fixed inclined place. A force F acts on block of mass m1 and is parallel to the inclined plane as shown in figure. Both blocks move up the incline. Then
(i) Draw free body diagram blocks of mass m1 and blocks mass m2
(ii) Find acceleration of blocks of mass m1 and blocks mass m2
(iii) Find normal reaction between the blocks of mass m1 and m2
View Solution