In the xy-plane, the graph of the polynomial function f crosses the x-axis at exactly two points, (a, 0) and (b, 0), where a and b are both positive. Which of the following could define f ?
f (x) = (x − a)(x − b)
f (x) = (x + a)(x + b)
f (x) = (x − a)(x + b)
f (x) = x(x − a)(x − b)
The correct Answer is:A
To determine which polynomial function f crosses the x-axis at exactly two points, (a,0) and (b,0), where both a and b are positive, we need to analyze the given options.
1. Understanding the Problem:
Since the polynomial crosses the x-axis at exactly two points, this means that f(a)=0 and f(b)=0. The polynomial must have roots at a and b and should not cross the x-axis at any other point.
2. Form of the Polynomial:
A polynomial that crosses the x-axis at two distinct points can be represented as:
f(x)=k(x−a)(x−b)
where k is a non-zero constant. This form ensures that the polynomial has roots at a and b.
3. Analyzing the Options:
We will evaluate each option to see if substituting a and b results in f(a)=0 and f(b)=0.
- Option A: Check if f(a)=0 and f(b)=0.
- Option B: Substitute a and b into the polynomial and check if it equals 0.
- Option C: Similarly, substitute a and b and check.
- Option D: Perform the same substitution.
4. Substituting Values:
- For each option, substitute a and b into the polynomial and check if the result is zero.
- If any option yields f(a)=0 and f(b)=0 without any additional roots, it is a candidate.
5. Identifying the Correct Option:
- After evaluating all options, we find that:
- Option A satisfies f(a)=0 and f(b)=0 without introducing any other roots.
- Other options either introduce additional roots or do not satisfy the conditions.
Conclusion:
The polynomial function f that crosses the x-axis at exactly two points (a,0) and (b,0) is defined by Option A.
Since the polynomial crosses the x-axis at exactly two points, this means that f(a)=0 and f(b)=0. The polynomial must have roots at a and b and should not cross the x-axis at any other point.
A polynomial that crosses the x-axis at two distinct points can be represented as:
f(x)=k(x−a)(x−b)
where k is a non-zero constant. This form ensures that the polynomial has roots at a and b.
We will evaluate each option to see if substituting a and b results in f(a)=0 and f(b)=0.
- Option B: Substitute a and b into the polynomial and check if it equals 0.
- Option C: Similarly, substitute a and b and check.
- Option D: Perform the same substitution.
- For each option, substitute a and b into the polynomial and check if the result is zero.
- If any option yields f(a)=0 and f(b)=0 without any additional roots, it is a candidate.
- After evaluating all options, we find that:
- Option A satisfies f(a)=0 and f(b)=0 without introducing any other roots.
- Other options either introduce additional roots or do not satisfy the conditions.
The polynomial function f that crosses the x-axis at exactly two points (a,0) and (b,0) is defined by Option A.
Similar Questions
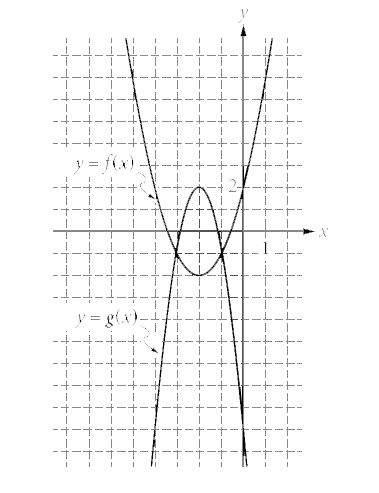
Graphs of the functions f and g are shown in the xy-plane above. For which of the following values of x does f(x)+g(x)=0 ?02:13View SolutionThe graph of the linear function f has intercepts at (a,0) and (0, b) in the xy-plane. If a+b=0 and a≠b, which of the following is true about the slope of the graph of f ?
05:22View Solutionf(x)=2x+1
The function f is defined by the equation above which of the following is the graph of y=−f(x) in the xy-plane?02:35View SolutionIf function f has exactly two distinct real zeros, which of the following graphs could be the complete graph of f (x) ?
01:35View SolutionThe function f(x)=4x2−25andg(x)=−4x2+25 are graphed in the xy-plane above. The point where the two functions intersect are (z,0) and (−z,0). What is the value of z ?
02:06View SolutionThe function f is defined by f(x)=x4−4x4−x2+cx−12 , where c is a constant.In the xy-plane, the graph of f intersects the x-axis in the four points (-2,0), (1,0), (p,0), and (q,0). What is the value of c ?
01:48View SolutionLet f (x) be a polynomial function of degree 3 where a<b<candf(a)=f(b)=f(c). If the graph of f (x) is as shown, which of the following statements are INCORRECT ? (Where c>|a|)
 View Solution
View SolutionDraw the graph of the polynomial f(x)=2x−5. Also, find the coordinates of the point where it crosses x-axis
02:18View Solution

