f (x) = (x + 3)(x − k)
T he function f is defined above. If k is a positive integer, which of the following could represent the graph of y = f (x) in the xy-plane?
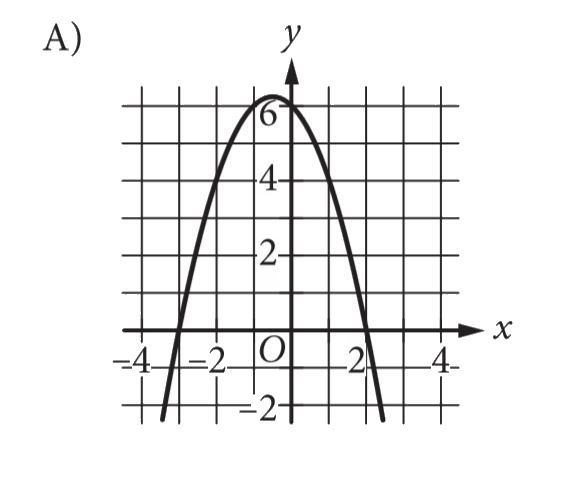
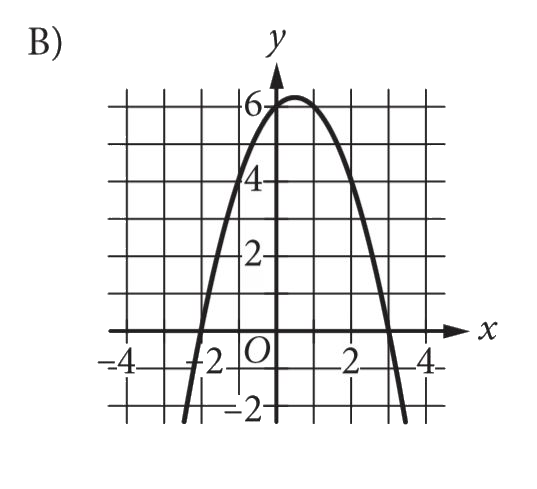
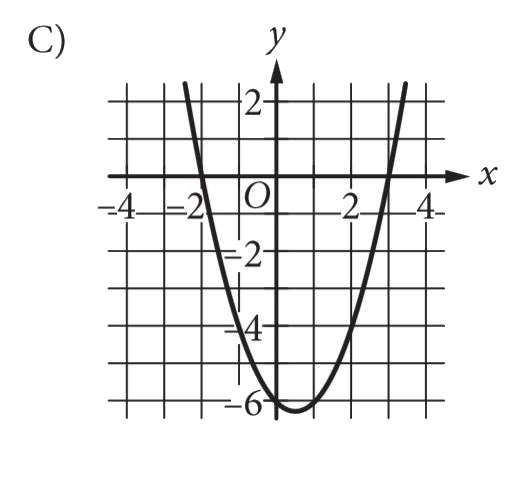
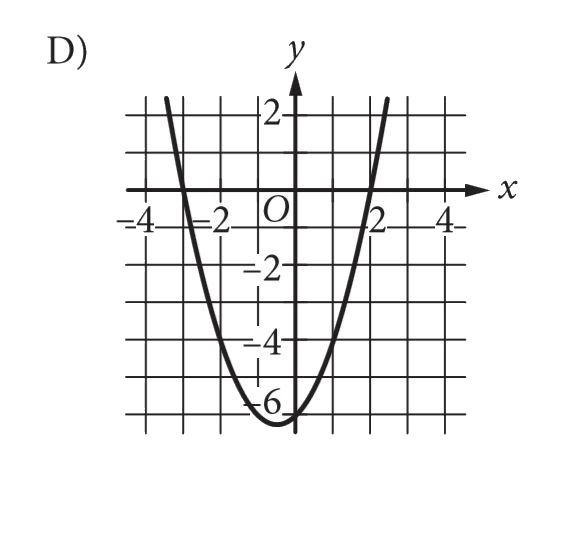
The correct Answer is:D
To solve the problem, we need to analyze the function f(x)=(x+3)(x−k) and determine the characteristics of its graph in the xy-plane.
Step 1: Expand the function
We start by expanding the function:
f(x)=(x+3)(x−k)=x2−kx+3x−3k
This simplifies to:
f(x)=x2+(3−k)x−3k
Step 2: Identify the type of function
The function f(x) is a quadratic function because it can be expressed in the form ax2+bx+c, where a=1, b=3−k, and c=−3k. Since a=1 is positive, the graph of this function will be a parabola that opens upwards.
Step 3: Find the roots of the function
To find the roots of the function, we set f(x)=0:
(x+3)(x−k)=0
This gives us the roots:
x+3=0⇒x=−3
x−k=0⇒x=k
Since k is a positive integer, the roots are x=−3 and x=k.
Step 4: Analyze the roots
The roots of the function are −3 and k. Since k is a positive integer, k will be greater than −3. Therefore, the graph will intersect the x-axis at −3 and at some positive value k.
Step 5: Determine the behavior of the graph
The vertex of the parabola will be located between the two roots. Since the parabola opens upwards, the vertex will be the minimum point of the graph. The y-intercept can be found by substituting x=0:
f(0)=(0+3)(0−k)=3(−k)=−3k
This means the graph will intersect the y-axis at −3k, which is negative since k is positive.
Step 6: Choose the correct graph
Given the characteristics of the graph:
- It opens upwards.
- It has roots at −3 and k (where k>0).
- It intersects the y-axis at a negative value.
We can now analyze the provided graphs to find one that meets these criteria.
Conclusion
The correct graph will be the one that:
- Opens upwards.
- Has a root at x=−3.
- Has another root at a positive value (greater than zero).
We start by expanding the function:
f(x)=(x+3)(x−k)=x2−kx+3x−3k
This simplifies to:
f(x)=x2+(3−k)x−3k
The function f(x) is a quadratic function because it can be expressed in the form ax2+bx+c, where a=1, b=3−k, and c=−3k. Since a=1 is positive, the graph of this function will be a parabola that opens upwards.
To find the roots of the function, we set f(x)=0:
(x+3)(x−k)=0
This gives us the roots:
x+3=0⇒x=−3
x−k=0⇒x=k
Since k is a positive integer, the roots are x=−3 and x=k.
The roots of the function are −3 and k. Since k is a positive integer, k will be greater than −3. Therefore, the graph will intersect the x-axis at −3 and at some positive value k.
The vertex of the parabola will be located between the two roots. Since the parabola opens upwards, the vertex will be the minimum point of the graph. The y-intercept can be found by substituting x=0:
f(0)=(0+3)(0−k)=3(−k)=−3k
This means the graph will intersect the y-axis at −3k, which is negative since k is positive.
Given the characteristics of the graph:
- It opens upwards.
- It has roots at −3 and k (where k>0).
- It intersects the y-axis at a negative value.
The correct graph will be the one that:
- Opens upwards.
- Has a root at x=−3.
- Has another root at a positive value (greater than zero).
Similar Questions
Knowledge Check
12 If the function f has five distinct zeros, which of the following could represent the complete graph of f in the xy‑plane?
A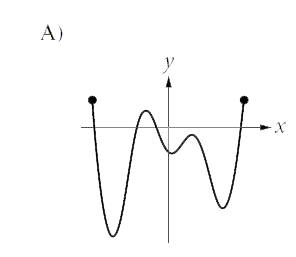 B
B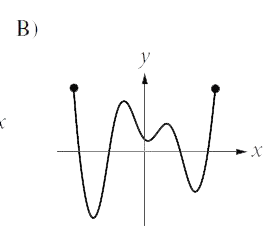 C
C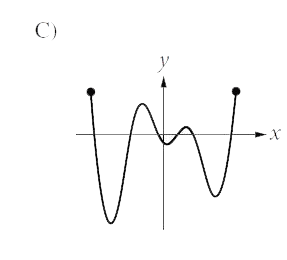 D
D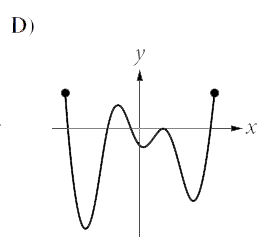

The graph of the function f is shown above. Which of the following could represent the graph of y=|f(x)|?A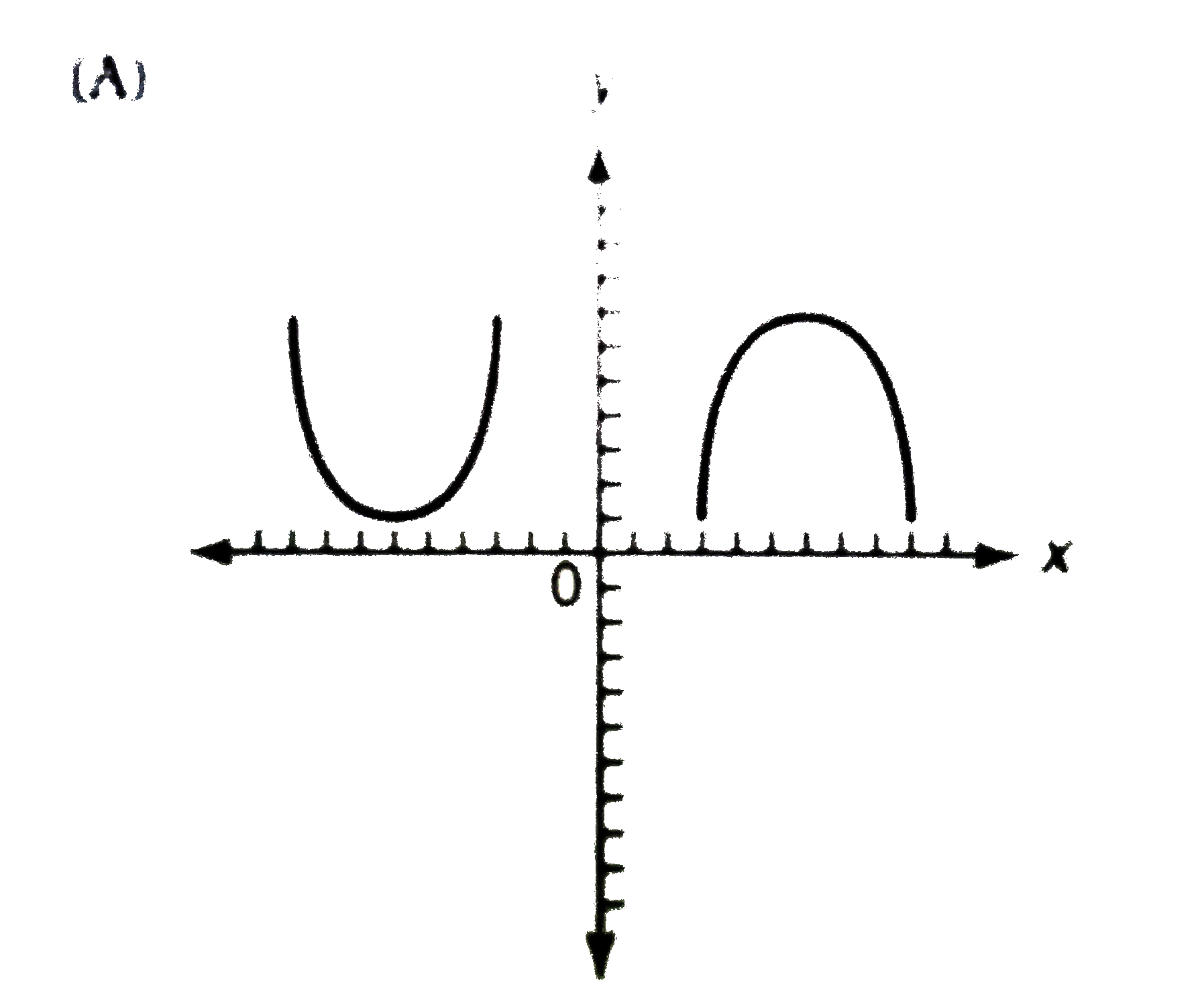 B
B C
C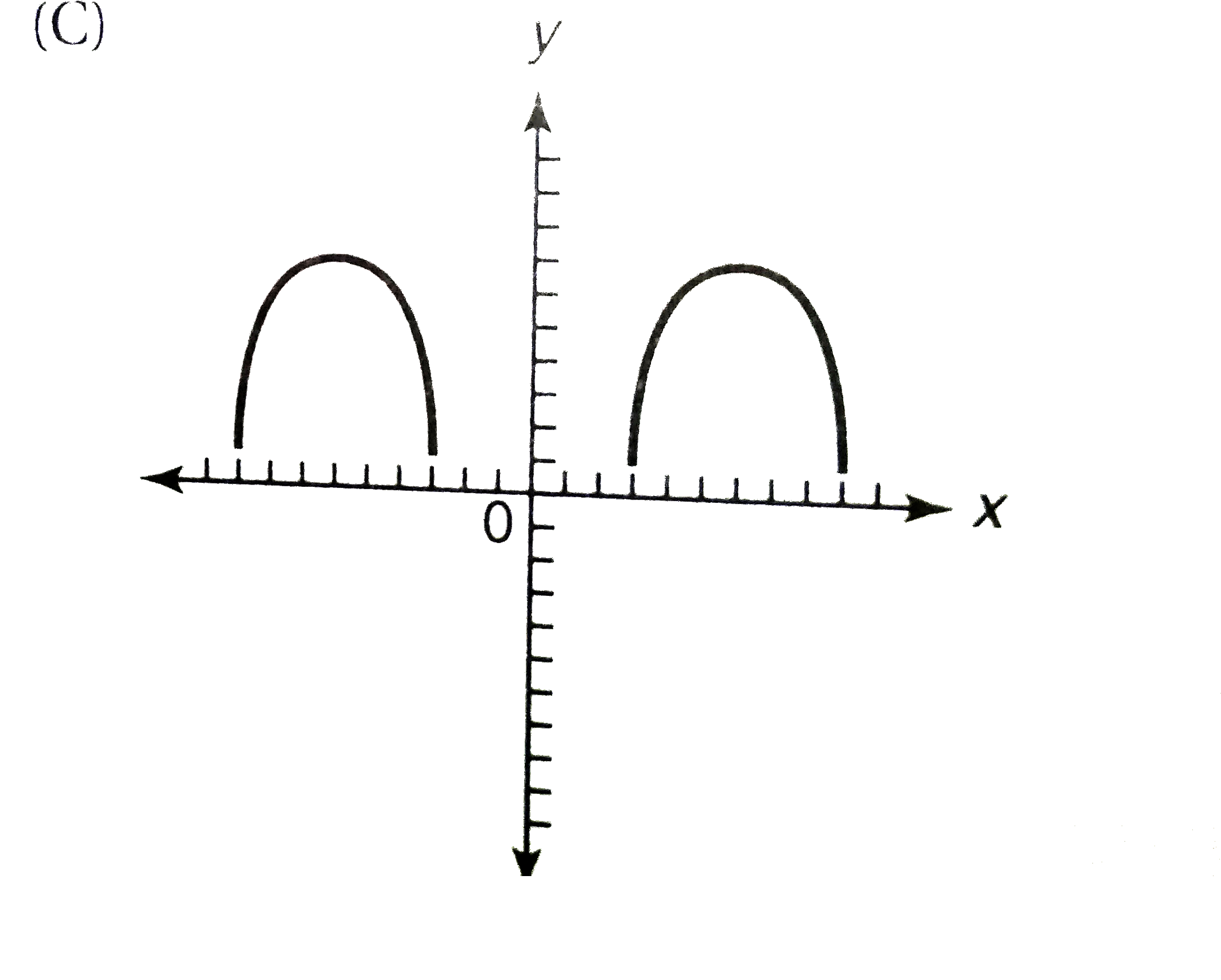 D
D
The graph of y=f(x) is shown below.
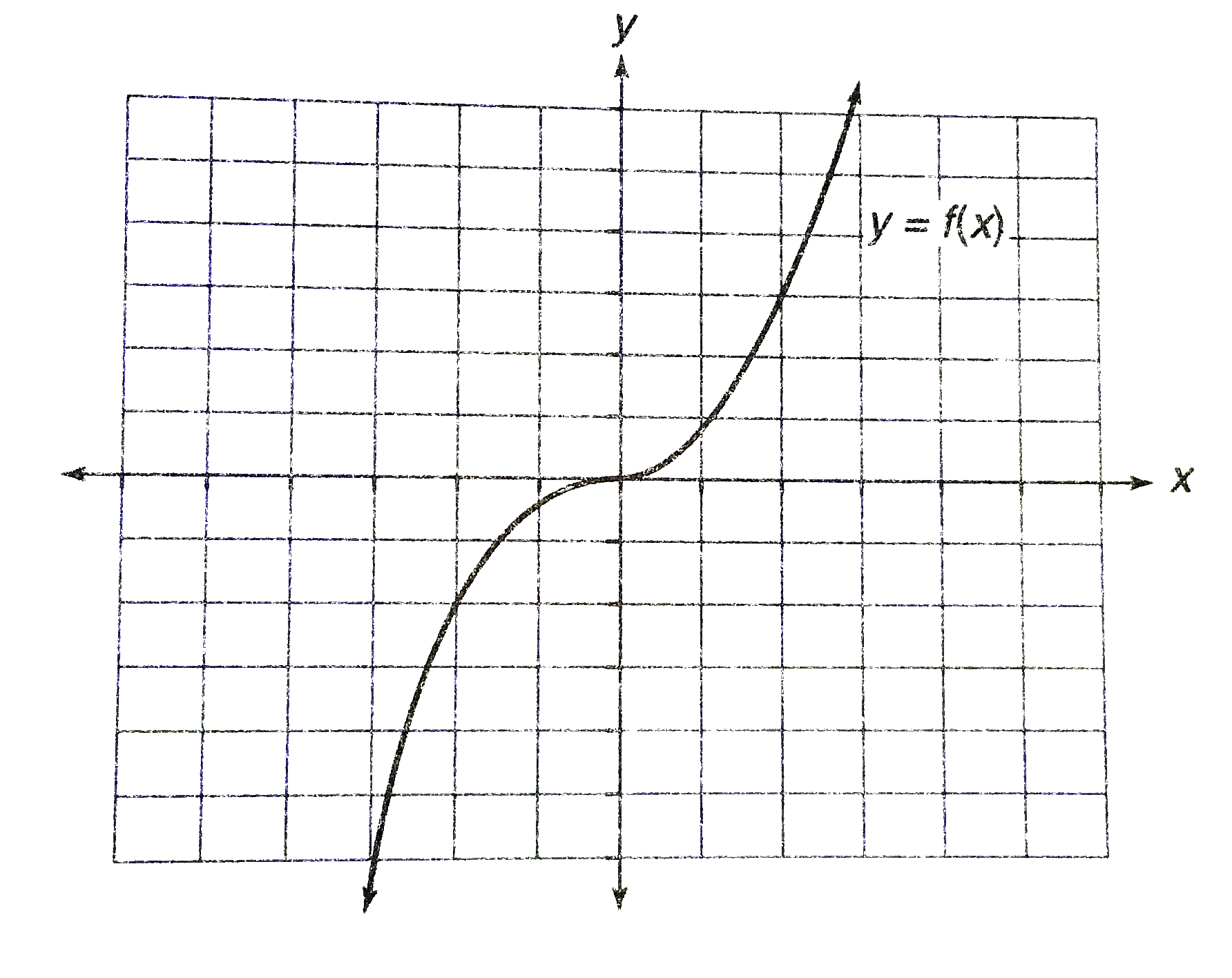
Which of the following could represents the graph of y=f(x−2)+1?A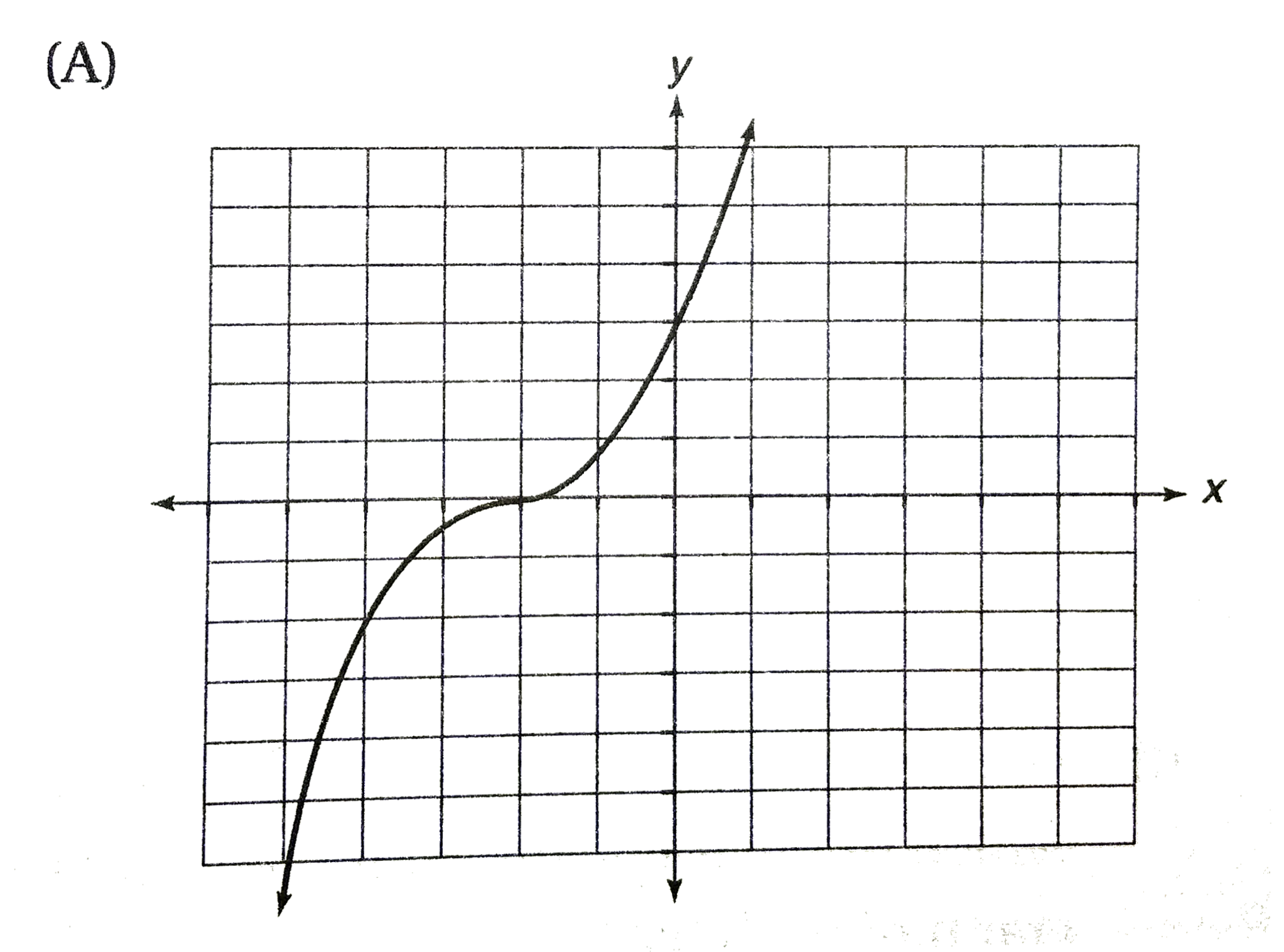 B
B C
C D
D
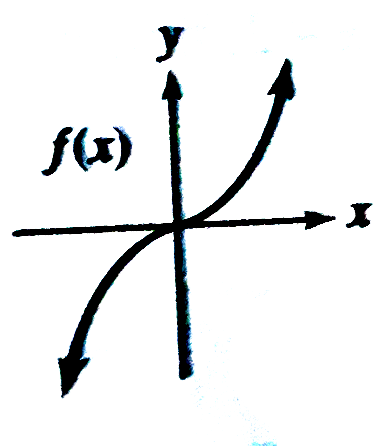
The graph of f(x) is shown above , Which of the following represents the graph of f(x-3) ?
View Solution
If the graph above is that of f(x), which of the following could be f(x)?
View SolutionIf function f has exactly two distinct real zeros, which of the following graphs could be the complete graph of f (x) ?
View SolutionIf f(x)=−x2 , which represents the graph of f(x)+3 ?
View SolutionThe range of the polynomial function f is the set of real numbers less than or equal to 4. If the zeros of f are −3 and 1, which of the following could be the graph of y = f (x) in the xy-plane?
View Solution

