R(r) is the radial part of the wave function and r is the distance of

Class 12 CHEMISTRY GRAPHICAL INTERPRETATION

Topper's Solved these Questions

GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Subjective Type
23 Videos
GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 29
1 Videos
F-BLOCK ELEMENTSBOOK - GRB PUBLICATIONCHAPTER - F-BLOCK ELEMENTSEXERCISE - Subjective type
7 Videos
HYDROCARBON (ALIPHATIC)BOOK - GRB PUBLICATIONCHAPTER - HYDROCARBON (ALIPHATIC)EXERCISE - Previous years jee questions
28 Videos

Knowledge Check

The Schrodinger wave equation for H-atom is
$\nabla^{2} Ψ = \frac{8 π^{2} m}{h^{2}} (E - V) Ψ = 0$
Where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$
E = Total energy and V=potential energy wave function $Ψ_{(\begin{matrix} r & θ & ϕ \end{matrix})} R_{(r)} Θ_{(θ)} Φ_{(ϕ)}$
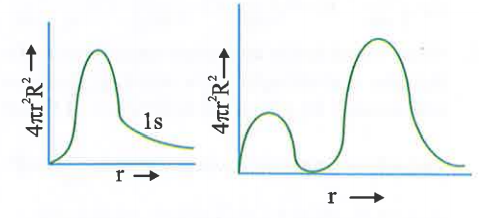
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. $Θ$ and $Φ$ are angular wave function. $R^{2}$ is known as radial probability density and $4 π r^{2} R^{2} d r$ is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
$Ψ_{1 s} = \sqrt{\frac{1}{π a_{0}^{a}}} e_{r}^{- z_{r} / a_{0}}$
$Ψ_{2 s} = {(\frac{Z}{2 a_{0}})}^{½} (1 - \frac{Z r}{a_{0}}) e^{- \frac{Z r}{a_{0}}}$
The plot of radial probability function $4 π r^{2} R^{2}$ aganist r will be:

Answer the following questions:
The following graph is plotted for ns-orbitals

The value of 'n' will be:
A1
B2
C3
D4
The Schrodinger wave equation for H-atom is
$\nabla^{2} Ψ = \frac{8 π^{2} m}{h^{2}} (E - V) Ψ = 0$
Where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$
E = Total energy and V=potential energy wave function $Ψ_{(\begin{matrix} r & θ & ϕ \end{matrix})} R_{(r)} Θ_{(θ)} Φ_{(ϕ)}$
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. $Θ$ and $Φ$ are angular wave function. $R^{2}$ is known as radial probability density and $4 π r^{2} R^{2} d r$ is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
$Ψ_{1 s} = \sqrt{\frac{1}{π a_{0}^{a}}} e_{r}^{- z_{r} / a_{0}}$
$Ψ_{2 s} = {(\frac{Z}{2 a_{0}})}^{½} (1 - \frac{Z r}{a_{0}}) e^{- \frac{Z r}{a_{0}}}$
The plot of radial probability function $4 π r^{2} R^{2}$ aganist r will be:

Answer the following questions:
The value of radius 'r' for 2s atomic orbital of H-atom at which the radial node will exist may be given as:
A $r = 2 a_{0}$
B $r = \frac{a_{0}}{4}$
C $r = a_{0}$
D $r = \frac{a_{0}}{5}$
The Schrodinger wave equation for H-atom is
$\nabla^{2} Ψ = \frac{8 π^{2} m}{h^{2}} (E - V) Ψ = 0$
Where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$
E = Total energy and V=potential energy wave function $Ψ_{(\begin{matrix} r & θ & ϕ \end{matrix})} R_{(r)} Θ_{(θ)} Φ_{(ϕ)}$
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. $Θ$ and $Φ$ are angular wave function. $R^{2}$ is known as radial probability density and $4 π r^{2} R^{2} d r$ is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
$Ψ_{1 s} = \sqrt{\frac{1}{π a_{0}^{a}}} e_{r}^{- z_{r} / a_{0}}$
$Ψ_{2 s} = {(\frac{Z}{2 a_{0}})}^{½} (1 - \frac{Z r}{a_{0}}) e^{- \frac{Z r}{a_{0}}}$
The plot of radial probability function $4 π r^{2} R^{2}$ aganist r will be:

Answer the following questions:
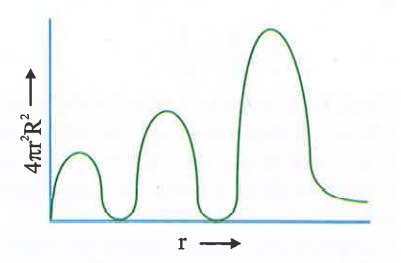
What will be number of angular nodes and spherical nodes for 4f atomic orbitals respectively.
A0,0
B1,3
C3,0
D0,3

R(r) is the radial part of the wave function and r is the distance of electron from the nucleus.

The correct Answer is:a-p; b-q; c-r,s,t; d-r,s,t

Topper's Solved these Questions

Similar Questions

Knowledge Check

GRB PUBLICATION-GRAPHICAL INTERPRETATION-Match The Column Type