A small block is rotating in a horizontal circle at the end of a thread which passes down through a hole at the centre of table top. If the system is rotating at 2.5 rps in a circle of 30 cm radius, what will be the speed of rotation when the thread is pulled inwards to decrease the radius to 10 cm ? Neglect friction.
Step by step video & image solution for A small block is rotating in a horizontal circle at the end of a thread which passes down through a hole at the centre of table top. If the system is rotating at 2.5 rps in a circle of 30 cm radius, what will be the speed of rotation when the thread is pulled inwards to decrease the radius to 10 cm ? Neglect friction. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem
24 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- PROPERTIES OF SOLIDSBOOK - SL ARORACHAPTER - PROPERTIES OF SOLIDSEXERCISE - All Questions
97 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
Similar Questions
A small block of mass m on a horizontal smooth table is attached to a light string passing through a hole as shown in the figure. Initially, the block moves in a circle of radius r with speed v and the string is held by a person. The person pulls the strin slowly to decrease the radius of circle to r/2. (a) Find the tension in the string when the block moves in a circle of radius r/2. (b) Calculate the change in the kinetic energy of the block.

View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View Solution
Knowledge Check
In the given figure, TB is a chord which passes through the centre of the circle . PT is a tangent to the circle at the point T on the circle . If PT=10cm, PA=5cm and AB=xcm, then the radius of the circle is :
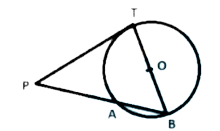 A5√3cmB6√5cmC3√5cmD10√3cm
A5√3cmB6√5cmC3√5cmD10√3cmA small stone of mass 50 g is rotated in a vertical circle of radius 40 cm. What is the minimum tension in the string at the lowest point?
A6NB2NC3ND1.5NA body of mass 1 kg is rotating in a verticle circle of radius 1 m .What will be the difference in its kinetic energy at the top and bottom of the circle ?
(g=10m/s2)A10 jB20 jC30 jD50 j
In the given figure, TB is a chord which passes through the centre of the circle. PT is a tangent to the circle at the point T on the circle. If PT = 10 cm, PA = 5 cm and AB = x cm. then the radius of the circle is:
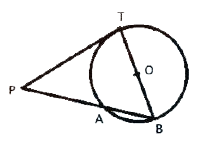
View SolutionA mass of 0.675 kg on a frictionless table is attached to a string which passes through a hole in the table at the centre. If the radius of the circle in which the mass rotates, is 5 m when its speed is 10ms−1, find the tension of the string. It is found that on drawing down the string by 0.2 m, the tension is increased 4.63 times. Calculate the work done by the string on the revolving mass during the reduction of the radius.
[Hint : Apply work-energy theorem to find work done by the force]
View SolutionA small block of mass 4 kg is attached to a cord passing through a hole in a horizontal frictionless syurface . The block is originally revolving in a circle of radius 0.5 m about the hole , with a tangential velocity of 4 m/s . The cord is then pulled slowly from below , shortening the radius of the circle in which the block revolves . The breaking strength of the cord is 600 N . What will be the radius of the circle when the cord breaks ?
View SolutionA small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius 0.5m about the hole with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shorting the radius of the circle in which the block revolves. The breaking strength of the cord is 600N. What will be radius of the circle when the cord breaks?

View SolutionA small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
What will be the radius of the circle when the cord breaks?
View Solution
