A small block of mass on a horizontal smooth table is attached to a light string passing through a hole as shown in the figure. Initially, the block moves in a circle of radius with speed and the string is held by a person. The person pulls the strin slowly to decrease the radius of circle to . (a) Find the tension in the string when the block moves in a circle of radius . (b) Calculate the change in the kinetic energy of the block.

The torque acting on the block about vertical axis through the hole is zero hence the angular momentum about this axis is constant. 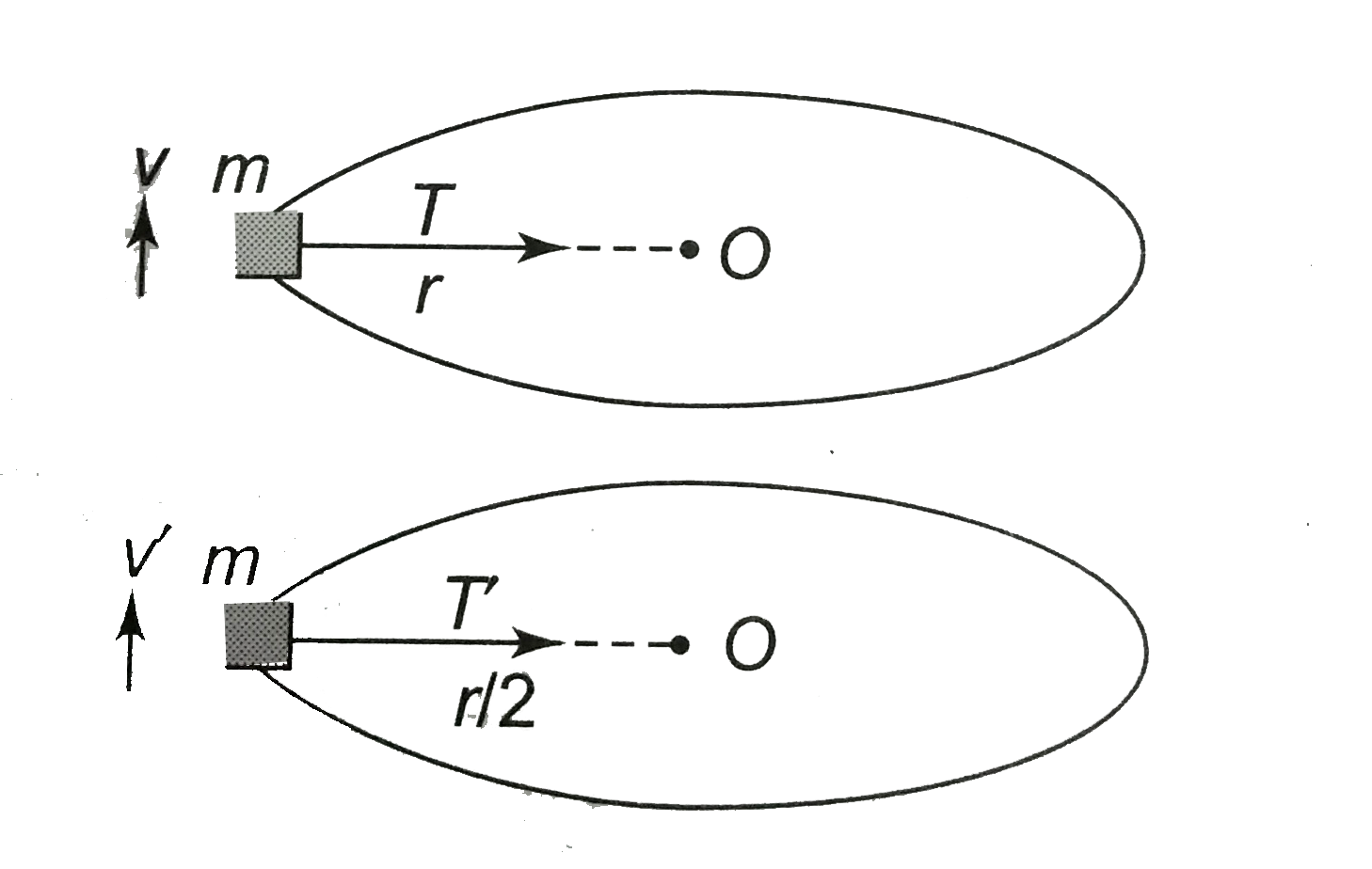
By the conservation of angular momentum
Tension provides necessary centripetal force
Topper's Solved these Questions
Similar Questions
Figure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA small block is rotating in a horizontal circle at the end of a thread which passes down through a hole at the centre of table top. If the system is rotating at 2.5 rps in a circle of 30 cm radius, what will be the speed of rotation when the thread is pulled inwards to decrease the radius to 10 cm ? Neglect friction.
View Solution
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
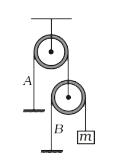 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgA block of mass m is moving in a circle of radius R with speed v inside a smooth cone as shown in figure. Choose the wrong options
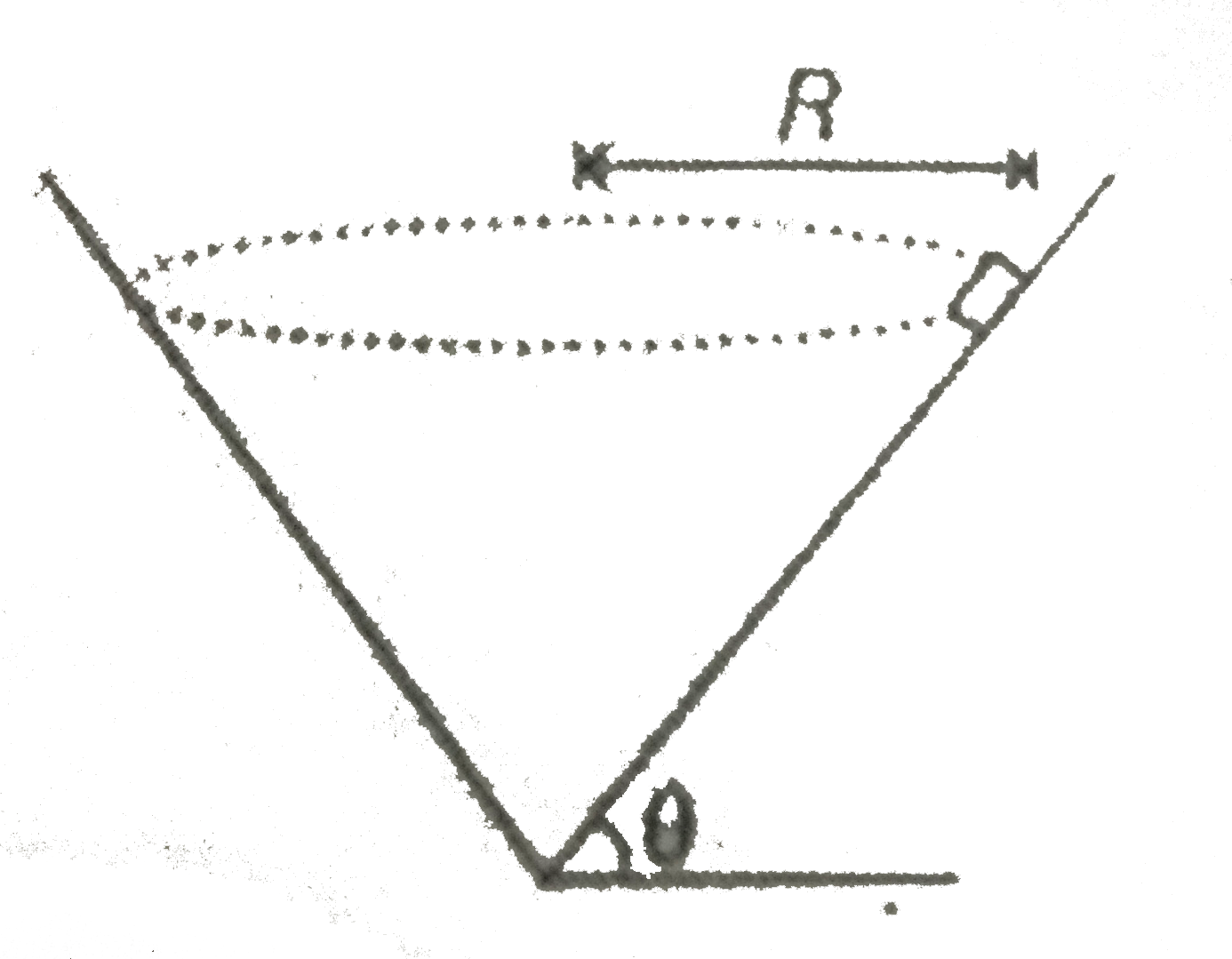 AN=0 if v=√RgtanθBNsinθ=mv2RCBlock is in equilibriumDBlock is accelerated
AN=0 if v=√RgtanθBNsinθ=mv2RCBlock is in equilibriumDBlock is acceleratedA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.
 AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
A paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View SolutionA block of mass m is supported by a string passing through a smooth peg as shown in the figure-2.130. Variation of tension in the string T as a function of θ best represented by (here the total length of the string is varied).
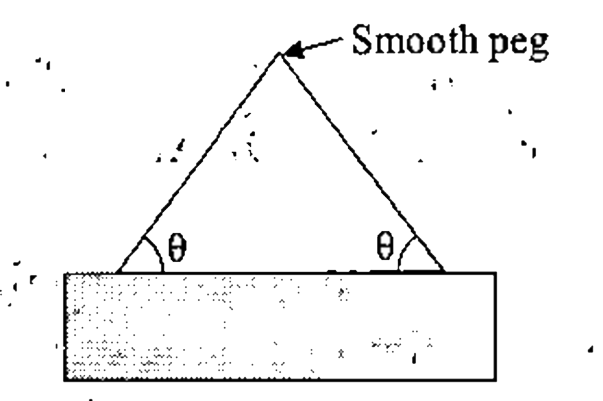
View SolutionA small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
Velocity of the block at the time of breaking of the string
View SolutionIn a conical pendulam, when the bob moves in a horizontal circle of radius r with uniform speed v, the string of length L describes a cone of semivertical angle θ. The tension in the string is given by
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View Solution

