The current density $¯ ¯ ¯ J$ inside a long, solid cylindrical wire of radius $a = 12 m m$ is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to $J = \frac{J_{0} r}{a}$ , where $J_{0} = \frac{10^{5}}{4 π} A / m^{2}$ . Find the magnitude of the magnetic field at $r = \frac{a}{2}$ in $μ T$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{μ_{0} i}{2 π a^{3}} r^{2}$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for The current density bar(J) inside a long, solid cylindrical wire of radius a = 12 mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J = (J_(0) r)/(a), where J_(0) = (10^(5))/(4 pi) A//m^(2). Find the magnitude of the magnetic field at r = (a)/(2) in mu T by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

For a long cylindrical wire of radius a=12 mm, we know that its current density $\to J$ is along the direction of the central axis and its magnitude varies linearly with radial distance r from the axis according to the relation $J = \frac{J_{0} r}{a}$ , where $J_{0} = \frac{10^{5}}{4 π} A / m^{2}$ . Calculate the magnitude of the magnetic induction at a position $r = \frac{a}{2}$ (in $μ T$ )
A10
B20
C30
D40
A current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius $R_{1}$ and outer radius $R_{2}$ . Magnetic field B varies with distance r form the axis of the cylinder is
A
B
C
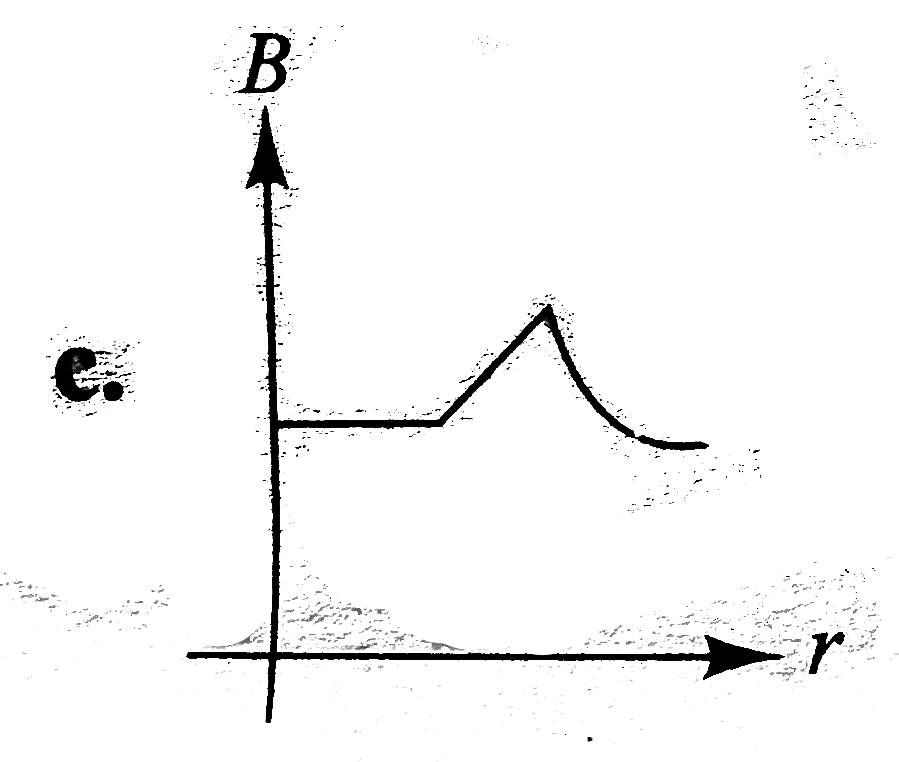D
The current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by $J (r) = J_{0} (1 - \frac{r}{R})$ . The total current in the radial regon r = 0 to $r = \frac{R}{4}$ will be :
A $\frac{5 J_{0} π R^{2}}{32}$
B $\frac{5 J_{0} π R^{2}}{96}$
C $\frac{3 J_{0} π R^{2}}{64}$
D $\frac{J_{0} π R^{3}}{128}$

NN GHOSH-INTRODUCTORY NOTES-Exercise

Home
Ask Doubt
Profile

The current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT

The correct Answer is:μ0i2πa3r2

Topper's Solved these Questions

Similar Questions

Knowledge Check

A current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius R1 and outer radius R2. Magnetic field B varies with distance r form the axis of the cylinder is

The current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r)=J0(1−rR) . The total current in the radial regon r = 0 to r=R4 will be :

NN GHOSH-INTRODUCTORY NOTES-Exercise

The correct Answer is: $\frac{μ_{0} i}{2 π a^{3}} r^{2}$

A current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius $R_{1}$ and outer radius $R_{2}$ . Magnetic field B varies with distance r form the axis of the cylinder is

The current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by $J (r) = J_{0} (1 - \frac{r}{R})$ . The total current in the radial regon r = 0 to $r = \frac{R}{4}$ will be :