Question

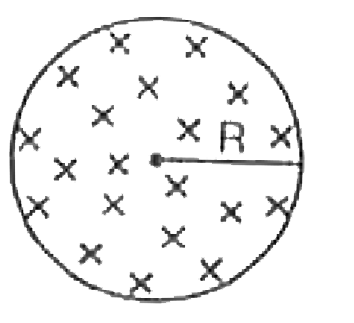
A cylindrical region of radius R contains a uniform magnetic field parallel to axis with magnitude that is changing linearly with time. If r is the radial distance of a point from axis of cylinder in a plane perpendicular to axis then the magnitude of the induced electrical field outside the cylinder is directly proportional to

Options

A. r
B. `r^2`
C. 1/r
D. `1//r^2`

Answer

C

Explanation

To solve the problem, we need to derive the relationship between the induced electric field (E) outside a cylindrical region with a changing magnetic field and the radial distance (r) from the axis of the cylinder.

1. Understanding the Setup:
- We have a cylindrical region of radius \( R \) with a uniform magnetic field \( B \) that is parallel to the axis of the cylinder.
- The magnetic field is changing linearly with time, which means \( B(t) = B_0 + kt \), where \( k \) is a constant and \( B_0 \) is the initial magnetic field.

2. Magnetic Flux Calculation:
- The magnetic flux \( \Phi_B \) through a circular area of radius \( r \) (where \( r > R \)) is given by:
\( \Phi_B = B \cdot A = B \cdot \pi r^2 \)
- Since the magnetic field is changing with time, we need to differentiate the flux with respect to time:
\( \frac{d\Phi_B}{dt} = \frac{d}{dt}(B \cdot \pi r^2) = \pi r^2 \frac{dB}{dt} \)

3. Induced EMF and Electric Field:
- According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) \( \mathcal{E} \) in a closed loop is related to the rate of change of magnetic flux:
\( \mathcal{E} = -\frac{d\Phi_B}{dt} \)
- Therefore, we have:
\( \mathcal{E} = -\pi r^2 \frac{dB}{dt} \)

4. Relating EMF to Electric Field:
- The induced EMF can also be expressed in terms of the electric field \( E \) around a circular loop of radius \( r \):
\( \mathcal{E} = \oint E \cdot dl = E \cdot 2\pi r \)
- Setting the two expressions for EMF equal gives:
\( E \cdot 2\pi r = -\pi r^2 \frac{dB}{dt} \)

5. Solving for the Induced Electric Field:
- Rearranging the equation to solve for \( E \):
\( E = -\frac{r}{2} \frac{dB}{dt} \)

6. Finding the Proportional Relationship:
- Since \( \frac{dB}{dt} \) is a constant (because the magnetic field is changing linearly with time), we can see that:
\( E \propto r \)
- Therefore, the magnitude of the induced electric field outside the cylinder is directly proportional to the radial distance \( r \).

Conclusion:
The magnitude of the induced electric field \( E \) outside the cylinder is directly proportional to the radial distance \( r \).