A block of mass m is pressed against a spring of force constant k. The block after leaving contact with the spring moves along a ''loop'' the loop track. The sliding surface is smooth except for rough portion of length s equal to R as shown in Fig. 3E.34, where the coefficient of friction is μk. Determine the minimum spring compression x for which the particle will not lose contant with the track ?

Step by step video & image solution for A block of mass m is pressed against a spring of force constant k. The block after leaving contact with the spring moves along a ''loop'' the loop track. The sliding surface is smooth except for rough portion of length s equal to R as shown in Fig. 3E.34, where the coefficient of friction is mu_(k). Determine the minimum spring compression x for which the particle will not lose contant with the track ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Level 1
Explore 53 Videos
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Level 2
Explore 18 Videos
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Matching types problems
Explore 14 Videos
- UNIT AND DIMENSIONSBook:ANURAG MISHRAChapter:UNIT AND DIMENSIONSExercise:Matching Type Problem
Explore 4 Videos
Similar Questions
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
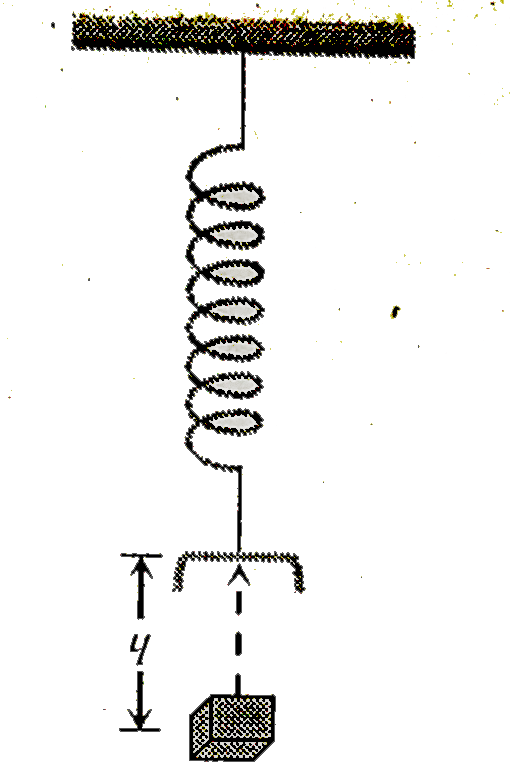
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
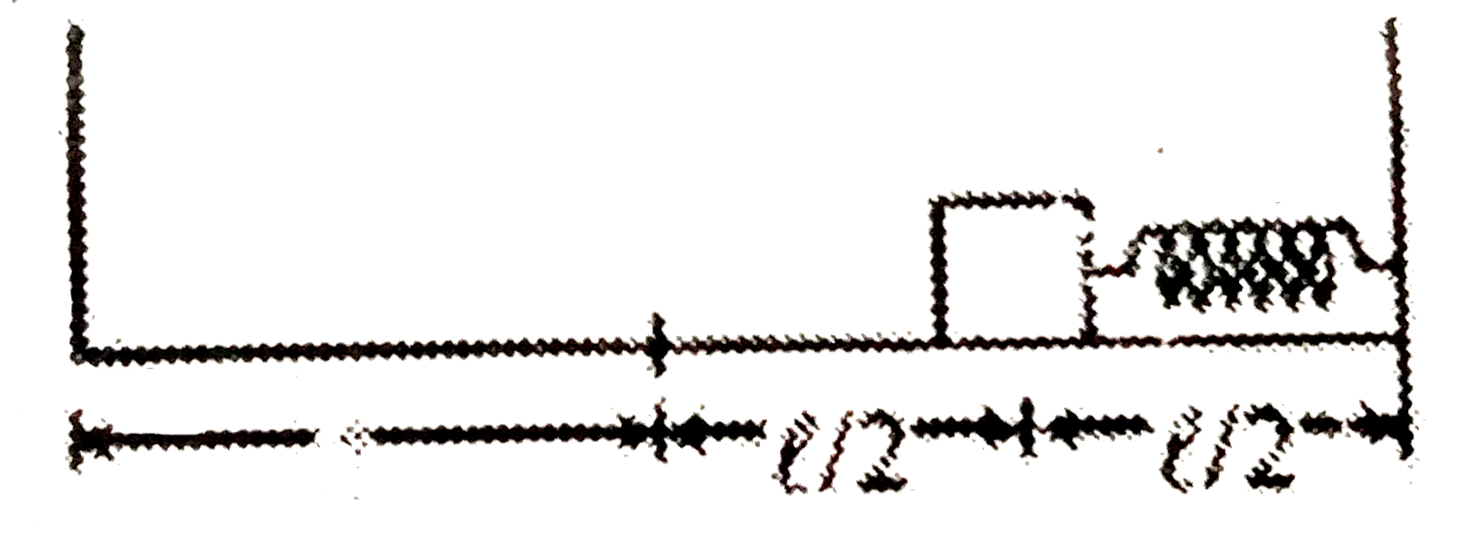 A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A2π√mkB(π+4)√mkC(1+π)√mkDNone of theseA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these
Block of mass m is pushed towards a horizontal spring as shown in figure , with initial speed u .

Spring constant of the spring is K and floor is smooth . Calculate maximum possible compression of the spring .
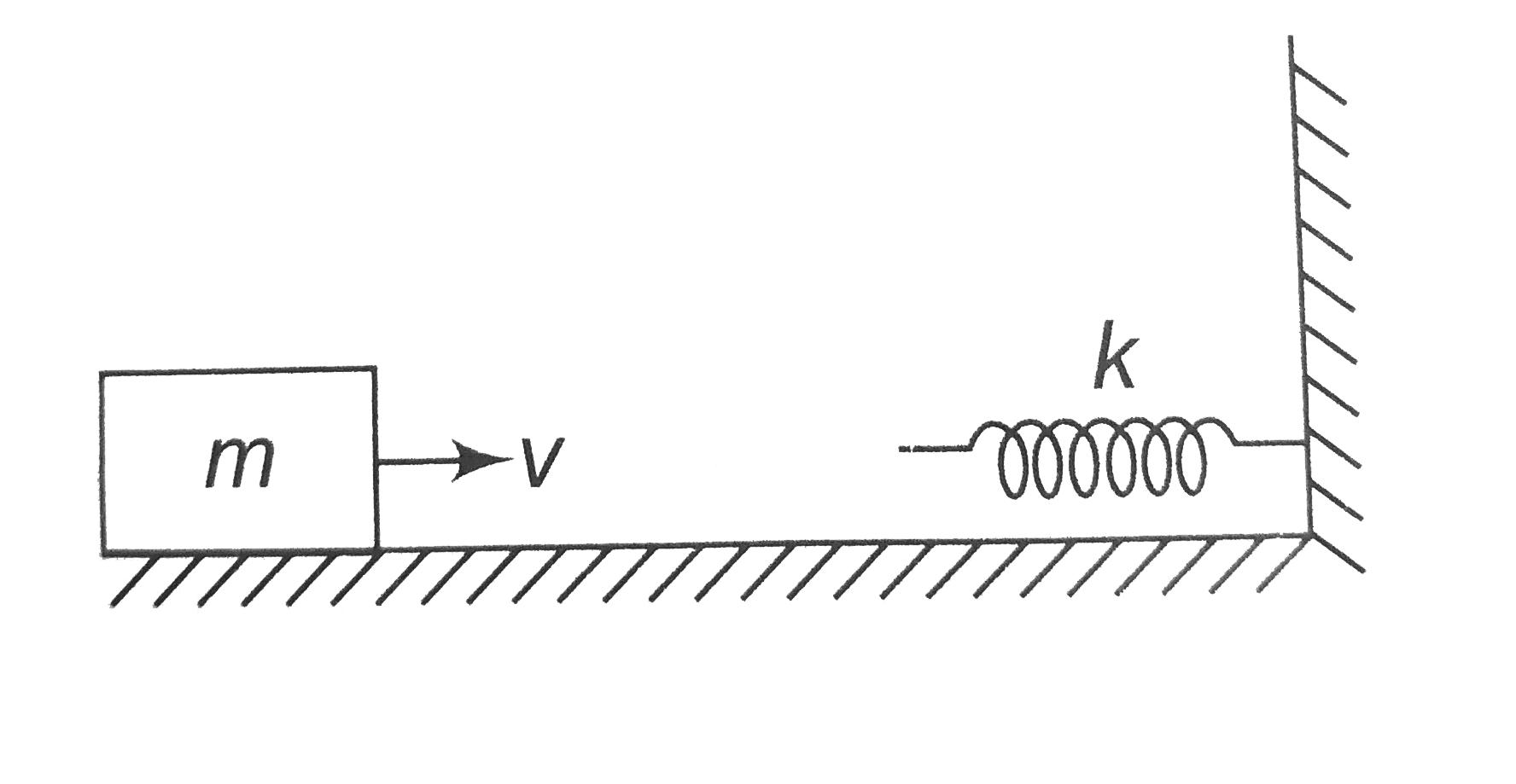
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
View SolutionA block of mass 1kg moves towards a spring of force constant 10N/m. The spring is massless and unstretched. The coeffcient of friction between block and surface is 0.30. After compressing the spring, block does not return back : (g=10m/s).
View SolutionA block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
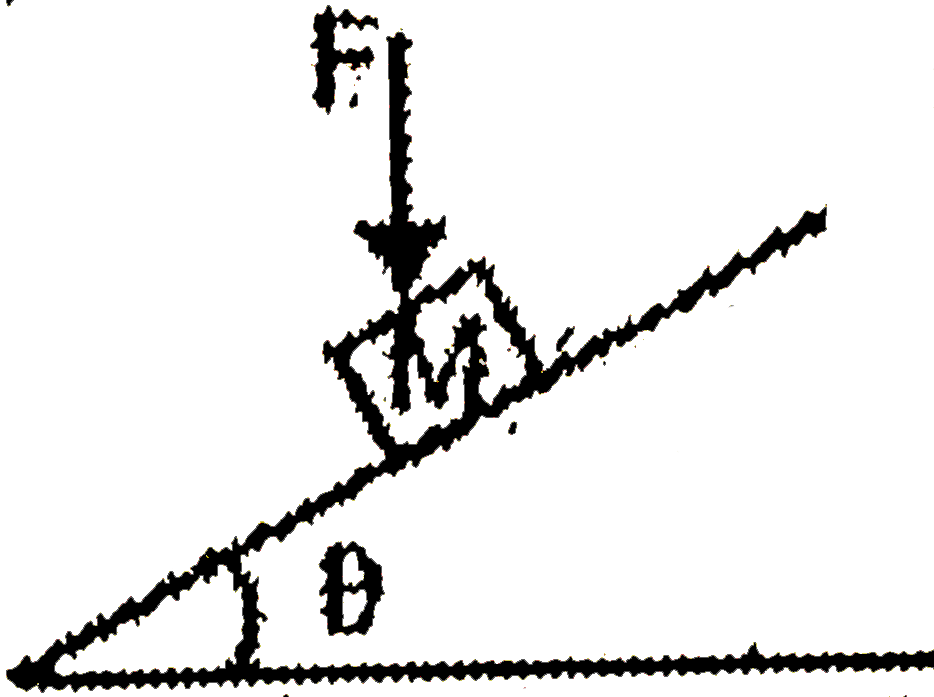
View SolutionA block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)

View Solution

