A block of mass 1kg moves towards a spring of force constant 10N/m. The spring is massless and unstretched. The coeffcient of friction between block and surface is 0.30. After compressing the spring, block does not return back : (g=10m/s).
the maximum value of speed of block for which it is possible is 3.8m/s
the maximum value of speed of block of which it is possible is 4.2m/s
if Ei and Ef are initial and final mechanical energy, which is sum of kinetic energy and potential energy, than work done by friction on a system is (Ei−Ef).
statement in option (C) is wrong.
The correct Answer is:A, C
The spring is compressed by x
Block will not return if μmg≥Kx
So, xmax=μmgK=(0.3)(1)(10)10=0.30m
work done against friction =Ei−Ef
μmg(x+2)=12mv20−12Kx2
(0.3)(1)(10)(0.3+2)=(12)(1)v20−(12)(10)(0.3)2
on solving, v0=3.8m/sec.
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Comprehension)
Explore 20 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Single Answer)
Explore 31 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
1 kg block collides with a horizontal massless spring of force constant 2N/m. The block compresses the spring by 4m. If the coefficient of kinetic friction between the block and the· surface is 0.25, what was the speed of the block at the instant of collision? (take g=10m/s2)

View SolutionA block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
 .
.
View Solution
Knowledge Check
A block mass m=2kg is moving with velocityv0 towards a massless unstretched spring of the force constant k=10N/m. Coefficient of friction between the block and the ground is μ=0.2. Find the maximum value of v0 so that after pressing the spring the block does not return back but stops there permanently.
 A2√25m/sB√15m/sC4√15m/sD4√25m/s
A2√25m/sB√15m/sC4√15m/sD4√25m/sA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of theseTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)g
Two blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant K=800N/m and the system is placed on a horizontal surface as shown.
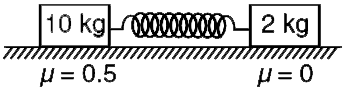
The coefficient of friction between 10 kg block and surface is 0.5 but friction is absent between 2 kg and the surface. Initially blocks are at rest and spring is relaxed. The 2 kg block is displaced to elongate the spring by 1 cm and is then released. (a) Will 10 kg block move subsequently? (b) Draw a graph representing variation of magnitude of frictional force on 10 kg block with time. Time t is measured from that instant when 2 kg block is released to move.
View SolutionTwo blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant 1000 N/m and the system is placed on a horizontal surface as shown. The coefficient of friction between 10 kg block and surface is 0.5 but friction is assumed to be absent between 2 kg and surface. Initially blocks are at rest and spring is unstretched then 2 kg block is displaced by 1 cm to elongate the spring then released. Then the graph representing magnitude of frictional force on 10 kg block and time t is : (Time t is measured from that instant when 2 kg block is released to move)
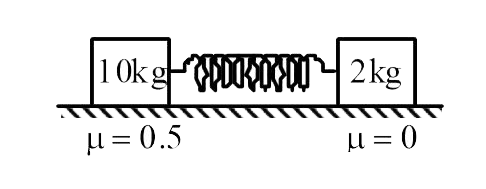
View SolutionA block of mass m=0.14kg is moving with velocity v0 towards a mass less unstretched spring of force constant K=10Nm−1. Coefficient of friction between the block and the ground is μ=1/2.

Find the maximum value of compression in the spring (in cm), so that after pressing the spring the block does not return back but stops there permanently.
View SolutionA block of mass 1 kg is suspended from a spring of constant 100 N/m. initially the spring is unstretched. The block is then released. What is the acceleration (in m/s2) of the block when its velocity is 0.6 m/s in the downwards direction ?
View SolutionA block of mass 0.18 kg is attached to a spring of force constant 2N/m. The coefficient of friction between the block and the floor is 0.1. Initially, the block is at rest and the spring is unstretched. An impulse is given to the block.
The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is v=N/10. Then, N is
View Solution

