Consider a cube having a uniform volume charge density. Find the ratio of electrostatic potential at the centre to the potential at a corner of the cube
2
√3/2
√2
1
The correct Answer is:A
Step by step video, text & image solution for Consider a cube having a uniform volume charge density. Find the ratio of electrostatic potential at the centre to the potential at a corner of the cube by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider a cube having a uniform volume charge density. Find the ratio of electrostatic potential at the centre to the potential at a corner of the cube
A2B√3/2C√2D1Consider a solid cube made up of insulating material having a uniform volume charge density. Assuming the electrostatic potential to be zero at infinity, the ratio of the potential at a corner of the cube to that at the centre will be
A1:1B1:2C1:4D1:8A non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
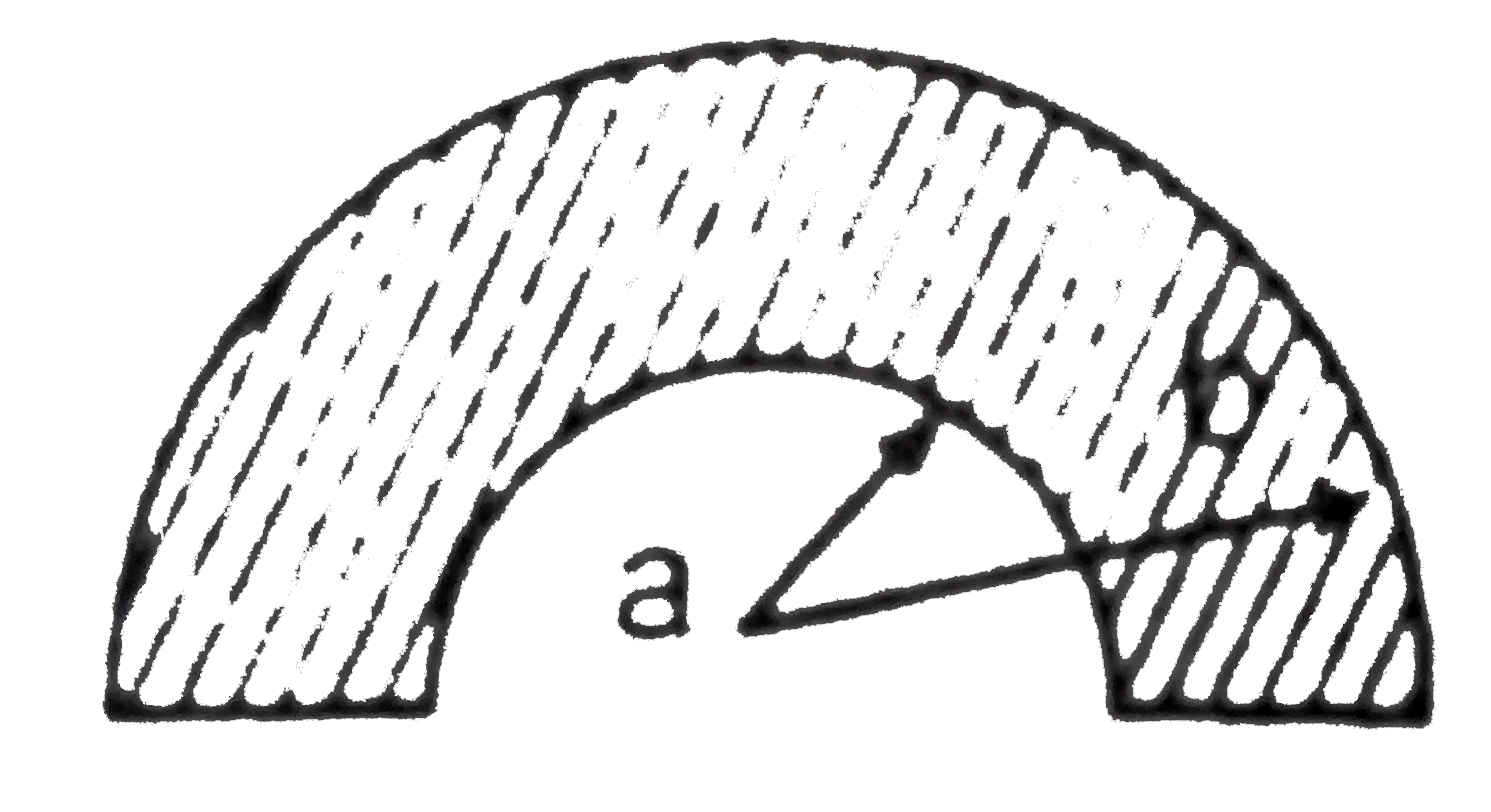 A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)
A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)
Two cubes have their volumes in the ratio 1 : 27. Find the ratio of their surface areas.
View SolutionA point charge q is kept at a corner of a cube
View SolutionThroughout the volume of the conductor, electrostatic potential is
View SolutionWhat is the ratio of the electrostatic potential at the corner and the centre point of a charged conducting cube? (The potential is considered 0 at infinity)
View SolutionA charge 'Q' is placed at each corner of a cube of side 'a'. The potential at the centre of the cube is
View Solution