Given a starting population of 100 bacteria, the formula b(t)=100(2t) can be used to determine the number of bacteria, b, after t periods of time. If each time period is 15 minutes long, how many minutes will it take for the population of bacteria to reach 51,200?
The correct Answer is:135
To solve the problem of how long it will take for a population of bacteria to reach 51,200 given the starting population and growth formula, we can follow these steps:
1. Understand the Growth Formula: The formula given for the bacteria population is:
b(t)=100×2t
where b(t) is the number of bacteria after t time periods.
2. Set Up the Equation: We need to find t when the population reaches 51,200. Therefore, we set up the equation:
51,200=100×2t
3. Divide Both Sides by 100: To isolate 2t, divide both sides of the equation by 100:
51,200100=2t
Simplifying the left side gives:
512=2t
4. Express 512 as a Power of 2: We need to express 512 as a power of 2. We know that:
512=29
Therefore, we can rewrite the equation as:
29=2t
5. Equate the Exponents: Since the bases are the same, we can equate the exponents:
t=9
6. Calculate the Total Time in Minutes: Each time period is 15 minutes long. To find the total time in minutes, multiply the number of time periods by the duration of each period:
Total time=15×t=15×9=135 minutes
Final Answer:
It will take 135 minutes for the population of bacteria to reach 51,200.
---
b(t)=100×2t
where b(t) is the number of bacteria after t time periods.
51,200=100×2t
51,200100=2t
Simplifying the left side gives:
512=2t
512=29
Therefore, we can rewrite the equation as:
29=2t
t=9
Total time=15×t=15×9=135 minutes
It will take 135 minutes for the population of bacteria to reach 51,200.
Topper's Solved these Questions
- PROBLEM SOLVING AND DATA ANALYSISBook:ENGLISH SATChapter:PROBLEM SOLVING AND DATA ANALYSISExercise:Multiple Choice
Explore 128 Videos
- PROBLEM SOLVING AND DATA ANALYSISBook:ENGLISH SATChapter:PROBLEM SOLVING AND DATA ANALYSISExercise:EXERICSE
Explore 80 Videos
- PROBLEMS IN CONTEXT Book:ENGLISH SATChapter:PROBLEMS IN CONTEXT Exercise:PRACTICE TEST
Explore 10 Videos
Similar Questions
An initial number of bacteria presented in a culture is 10000. This number doubles every 30 minutes. How long will it take to bacteria to reach the number 100000 ?
View SolutionThe rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given the number triples in 5 hrs., find how many bacteria will be present after 10 hours. Also find the time necessary for the number of bacteria to be 10 times the number of initial present. [Given loge3=1.0986, e2.1972=9 ]
View Solution
Knowledge Check
A population, T(x), of wild turkeys, in a certain rural area is represented by the function, T(x)=17(1.15)2x, where x is number of years since 2010. According to this model, how many more turkeys are in the population for the year 2015 than were avaible for 2010?
A46B49C51D68Two hoses attached to separate water sources are available to fill a cyindrical swimming pool. If both hoses are used , the time it will take to fill the pool can be represented by the following equation : 1T1+1T2=1Tc, where T1andT2 represent the time needed for hoses 1 and 2 , respectively , to fill the pool on their own , and Tc represents the time needed for hoses 1 and 2 to fill the pool working together . IF hose 1 alone can fill the pool in exactly 20 minutes and hose 2 alone can fill the pool in exactly 60 minutes , how many minutes will it take to fill the pool if both hoses work simultaneously ?
A3B10C15D18Cost is expressed by the formula tb4. If b is doubled and t remains the same, the new cost is how many times greater than the original cost?
A1.2B2C6D16
n=12×2t3
The number of mice in a certain colony is shown by the formula above, such that n is the number of mice and t is the time, in months, since the start of the colony. IF 2 years have passed since the start of the colony, how many mice does the colony contain now?
View SolutionIn the circuit shown in fig switch S is closed at time t =0.

a. What is the current I0 leacing the battery at t=0, immediately after the switch is closed?
b. What is the current I "long time" later?
c. What charge has accmulated on the capacitor after this long time?
d. If, finally, swtich S is opened again, how long will it take after the switch is opened for the capactior to lose 80% of its charge?
View SolutionA biologist places a colony consisting of 5000 bacteria into a petri dish. After the intial placement of the bacteria at time t = 0, the biologist measures and estimates the number of bacteria present every half hour. This data was then fitted by an exponential curve of the form y=c.2kt where c and k are constants, t is measured in hours, and y is measured in thousands of bacteria. The scatterplot together with the exponential curve are shown below.
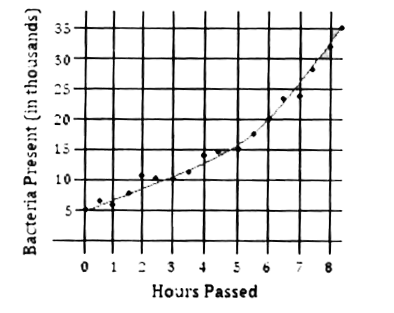
According to the scatterplot, the biologist'smeasurements indicate that the number of bacteria present quadrupled in 6 hours, and the exponential curve passes through the corresponding data point at time t = 6. The exponential function also agrees with the initial number of bacteria. Compute ck.
View Solution50t+3c=300
Robert is playing blackjack at a casino. The equation above can be used to model the number of chips, c, that Robert still has in his possession t hours after he begins playing. What does it mean that t=0,c=100 is a solution to this equation?
(A) Robert is losing 10 chips per hour.
(B) It would take 100 hours for robert to have 300 chips.
(C) Robert can play for 100 hours before losing all his chips.
(D) Robert begins playing with 100 chips.
View SolutionMiriam and Jessica are growing bacteria in a laboratory. Miriam uses the growth function f(t)=n2t to model her experiment while Jessica uses the function g(t)=(n2)4t to model her experiment. In each case, n represents the initial number of bacteria, and t is the time, in hours. If Miriam starts with 6 bacteria, how many bacteria should Jessica start with to achieve the same growth over time?
View Solution

