The figure shows a rod which startsm rotating with angular acceleration α about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass m just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient μ. As the angular velocity of rod increases the bead starts sliding over the rod (say after time t0)

Based on above information answer the following question :
Friction force acting on bead at time t(<t0) is given by :
μmg
mr(αt)2
mμ√g2+(rα)2
μm√g2+r2(αt)4
The correct Answer is:b
Step by step video, text & image solution for The figure shows a rod which startsm rotating with angular acceleration alpha about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass m just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient mu. As the angular velocity of rod increases the bead starts sliding over the rod (say after time t_(0)) Based on above information answer the following question : Friction force acting on bead at time t( lt t_(0)) is given by : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Level-2
Explore 73 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
Similar Questions
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution
Knowledge Check
The figure shows a rod which startsm rotating with angular acceleration α about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass m just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient μ. As the angular velocity of rod increases the bead starts sliding over the rod (say after time t0)
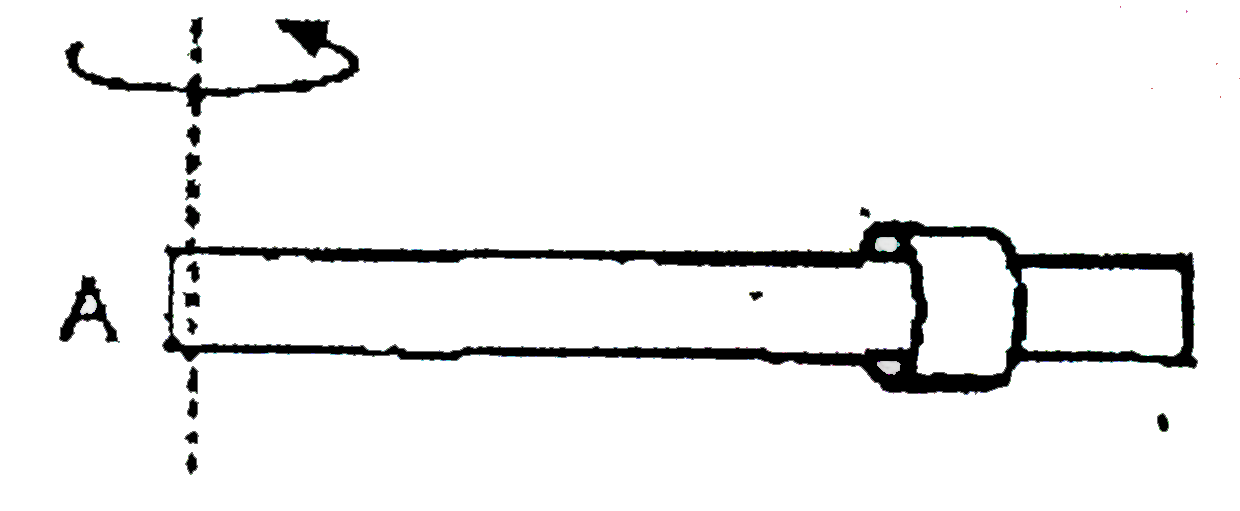
Based on above information answer the following question :
The normal force acting on bead at time t(<t0) is :AmgBmr(αt)2Cm√g2+r2(αt)4Dm√g2+(rα)2The figure shows a rod which startsm rotating with angular acceleration α about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass m just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient μ. As the angular velocity of rod increases the bead starts sliding over the rod (say after time t0)
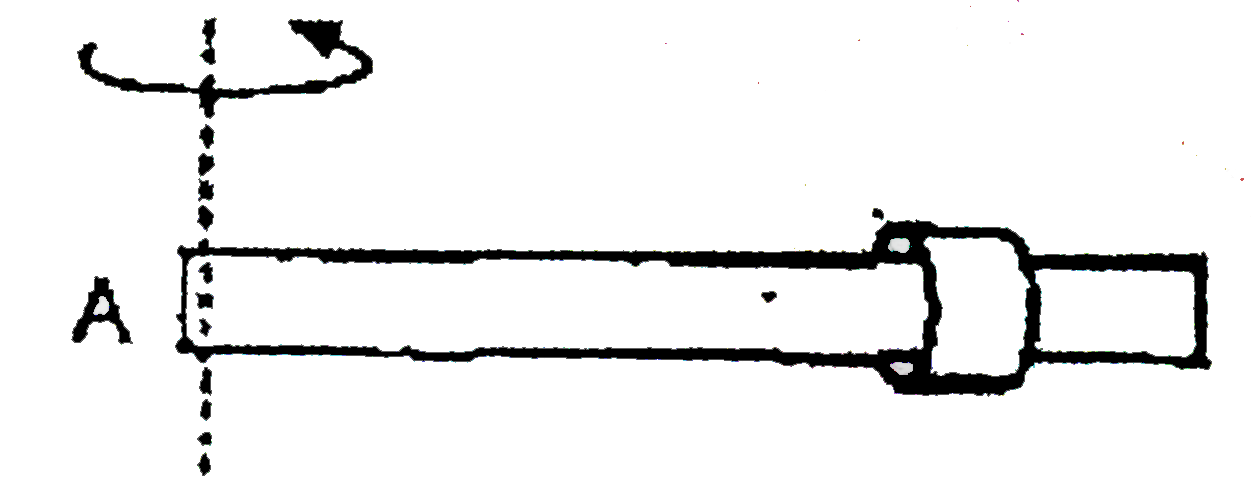
Based on above information answer the following question :
If the bead start sliding at t=t0 then value of t0 is given by :A ⎷μ√g2+(rα)2rα2B√mgrα2C ⎷μ√g2+(rα)2rα2−√mgrα2DNone of theseA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotation
A uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration
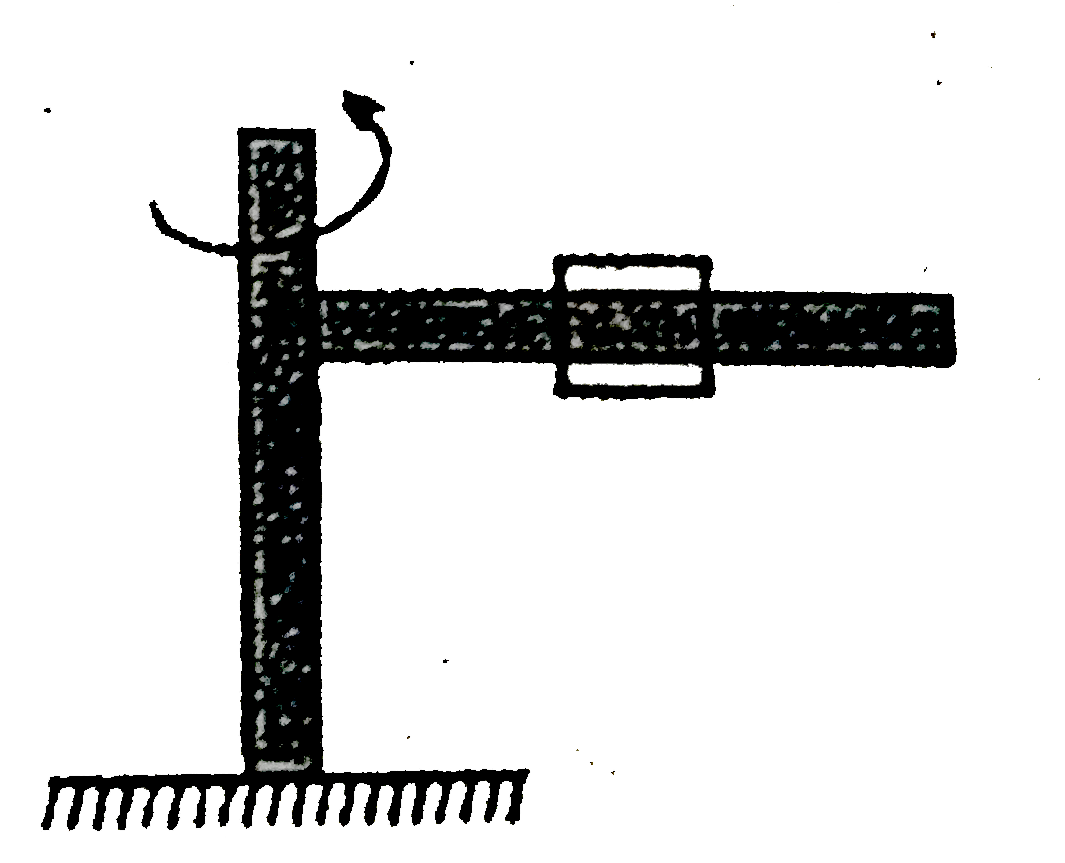
View SolutionA thin rod AB of mass M and length L is rotating with angular speed ω0 about vertically axis passing through its ends B on a horizontal smooth table as shown. If at some instant the hinge at end B of rod is opened then which of the following statemtents is / are correct about motion of rod?

View SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is
View Solution

